
Concept explainers
(a)
Find the angular acceleration of each cylinder
(a)
Answer to Problem 16.45P
The angular acceleration of each cylinder
Explanation of Solution
The weight of the cylinder A
The weight of the cylinder B
The weight of the cylinder C
The initial angular velocity of the cylinder A
The coefficient of the kinetic friction
The radius of the cylinder A
The radius of the cylinder B
The radius of the cylinder C
Calculation:
Consider the acceleration due to gravity (g) as
Convert the unit of the radius of the cylinder A
Convert the unit of the radius of the cylinder B
Convert the unit of the radius of the cylinder C
Calculate the mass of the cylinder A
Substitute
Calculate the mass of the cylinder B
Substitute
Calculate the mass of the cylinder C
Substitute
Calculate the mass moment of inertia of the cylinder A
Substitute
Calculate the mass moment of inertia of the cylinder B
Substitute
Calculate the mass moment of inertia of the cylinder C
Substitute
Calculate the tangential acceleration of contact point between cylinder B and C
Here,
The friction force at the contact point between cylinder A and C
Show the free body diagram of the cylinder B as in Figure 1.
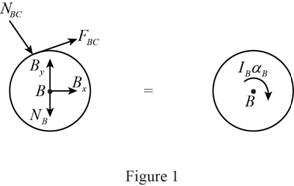
Here,
Refer to Figure 1.
Calculate the moment about point B by applying the equation of equilibrium:
Substitute
Show the free body diagram of the cylinder C as in Figure 2.
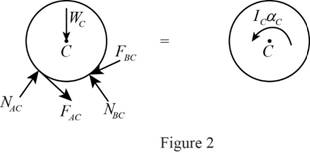
Here,
Refer to Figure 2.
Calculate the moment about point C by applying the equation of equilibrium:
Substitute
Calculate the normal force at the contact point between cylinder A and C
Substitute
Consider that the contact point between cylinder A and C is P.
Calculate the components of forces acting along the line CP:
Calculate the angular acceleration of the cylinder C
Substitute
Calculate the friction force at the contact point between cylinder A and C
Substitute
Calculate the friction force at the contact point between cylinder B and C
Substitute
Calculate the normal force at the contact point between cylinder A and C
Substitute
Show the free body diagram of the cylinder A as in Figure 3.
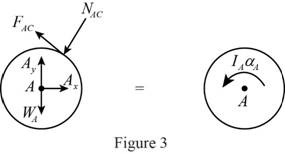
Here,
Refer to Figure 3.
Consider that the contact point between cylinder B and C is Q.
Calculate the components of forces acting along the line CQ:
Calculate the normal force at the contact point between cylinder B and C
Substitute
Calculate the angular acceleration of the cylinder A
Calculate the moment about point A by applying the equation of equilibrium:
Substitute
Calculate the angular acceleration of the cylinder A
Substitute
Hence, the angular acceleration of each cylinder
(b)
Find the final angular velocity of each disk
(b)
Answer to Problem 16.45P
The final angular velocity of each disk
Explanation of Solution
The weight of the cylinder A
The weight of the cylinder B
The weight of the cylinder C
The initial angular velocity of the cylinder A
The coefficient of the kinetic friction
The radius of the cylinder A
The radius of the cylinder B
The radius of the cylinder C
Calculation:
Refer to part (a).
The convert the unit of the initial angular velocity of the disk A
Calculate the angular velocity of cylinder A
Substitute
Calculate the tangential velocity of cylinder A
Substitute
Calculate the angular velocity of cylinder C
Substitute
Calculate the tangential velocity of cylinder C
Substitute
Calculate the time taken when tangential velocities are equal:
Substitute
Calculate the final angular velocity of the disk A
Substitute
Calculate the final angular velocity of the disk C
Substitute
Calculate the final angular velocity of the disk B
Substitute
Hence, the final angular velocity of each disk
Want to see more full solutions like this?
Chapter 16 Solutions
VECTOR MECHANIC
- Show work if any equations or calculations are used. Assuming hole basis, find the shaft and hole dimensions for a sliding fit using a basic hole size of 20mm. Show the max and minimum size for both hole and shaft. Utilize the equations and tables in the appendix.arrow_forwardShow work if any equations or calculations are used. A milling machine is equipped with a 1” diameter end mill. During a facingoperation, the spindle is running at 275 RPM. The depth of cut is 0.04” and linear feed rate is 2” per minute. Find: (a) Cutting speed, (b) Material Removal Ratearrow_forwardL1 = 5.7m, L2 = 1m, L3 = 1.2m, L4 = 1m, L5 = 0.2, L6 = 0.5m, v2 = 4.8m/s. The solutions should include, but not be limited to, the equations used tosolve the problems, the charts used to solve the problems, detailed working,choice of variables, the control volume considered, justification anddiscussion of results etc.If determining the friction factor, the use of both Moody chart and empiricalequations should be used to verify the validity of the valuearrow_forward
- Please identify the marked points of the stress-strain curve (Write on graph next to corresponding letter) Stress, σ A D (slope of line) B. C Strain, &arrow_forwardr Q2. A bracket is attached to a vertical column by means of six identical bolts as shown in Fig. 1. It is subjected to an eccentric force of P-80 kN at a distance of 200 mm from the center of column. What is the magnitude of maximum shear force and which bolt carry it? P= 80 kN 200 Fig. 1 1 2- 75 6 30 75 → 5 .5 1- 50 10-50-1arrow_forward3. The attachment shown in the Fig.2 is made of 1040 HR. The static force is 30 kN. Specify the weldment (give the pattern, electrode number, type of weld, length of weld, and leg size). 30 kN Fig. 2 500 All dimension in mm 100 (15 marks)arrow_forward
- ฉันต้องการหา อุณหภูมิสุดท้ายของกระบวนการนี้และงานของกระบวนการนี้มีค่าเท่าใดarrow_forwardThe pressure and temperature at the beginning of compression of a cold air-standard Diesel cycle are 100 kPa and 300 K , respectively. At the end of the heat addition, the divssure is 7.2 MPa and the temperature is 2050 K . Assume constant specific heats evaluated at 300 K . Determine:(a) the compression ratio.(b) the cutoff ratio.(c) the percent thermal efficiency of the cycle.(d) the mean effective pressure, in kPa .arrow_forwardQ3. Determine the reaction force at A and force P applied at 45° to the horizontal just necessary to start a roller 100 cm diameter over an obstruction 25 cm high, if the roller weighs 1000 N, as shown in Fig. 3. Fig. (3)arrow_forward
- Correct Answer is written below(preferably handwritten solution) . Detailed and complete fbd only please. I will upvote, thank you.arrow_forwardThe pressure and temperature at the beginning of compression of a cold air-standard Diesel cycle are 100 kPa and 300 K , respectively. At the end of the heat addition, the pressure is 7.2 MPa and the temperature is 2050 K . Assume constant specific heats evaluated at 300 K . Determine:(a) the compression ratio.(b) the cutoff ratio.(c) the percent thermal efficiency of the cycle.(d) the mean effective pressure, in kPaarrow_forwardCorrect Answer is written below(preferably handwritten solution) . Detailed and complete fbd only please. I will upvote, thank you.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





