
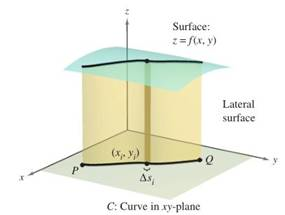
Lateral Surface Area In Exercises 65–-72, find the area ofthe lateral surface (see figure) over the curve C in the x y-plane and under the surface
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
Calculus: Early Transcendental Functions (MindTap Course List)
- the correct answer is A could you show me whyarrow_forwardGood Day, Kindly assist me with this query.arrow_forwardon donne f(x) da fonction derive dhe do fonction fcsos calcule f'(x) orans chacun des Cas sulants: 3 1) f(x)=5x-11, 2- f (x) = ->³ 3-1(x) = x² 12x +π; 4-f(x)=- 5-f(x) = 33-4x6-609)=-3x²+ 7= f(x) = x + 1.8-f(x) = 4 s-f(x) = x++ X+1 -x-1 2 I 3x-4 девоarrow_forward
- The correct answer is Ccould you show me how to do it by finding a0 and and akas well as setting up the piecewise function and integratingarrow_forwardT 1 7. Fill in the blanks to write the calculus problem that would result in the following integral (do not evaluate the interval). Draw a graph representing the problem. So π/2 2 2πxcosx dx Find the volume of the solid obtained when the region under the curve on the interval is rotated about the axis.arrow_forward38,189 5. Draw a detailed graph to and set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the curve: y = cos²x_for_ |x| ≤ and the curve y y = about the line x = =플 2 80 F3 a FEB 9 2 7 0 MacBook Air 3 2 stv DGarrow_forward
- Find f(x) and g(x) such that h(x) = (fog)(x) and g(x) = 3 - 5x. h(x) = (3 –5x)3 – 7(3 −5x)2 + 3(3 −5x) – 1 - - - f(x) = ☐arrow_forwardx-4 Let f(x)=5x-1, h(x) = Find (fo h)(0). 3 (fo h)(0) = (Type an integer or a fraction.)arrow_forwardFill in the blanks to write the calculus problem that would result in the following integral (do not evaluate the interval). Draw a graph representing the problem. π/2 So/² 2xcosx dx Find the volume of the solid obtained when the region under the curve 38,189 on the interval is rotated about the axis.arrow_forward
- Let f(x) = -5x-1, g(x) = x² + 5, h(x) = · x+4 3 Find (hog of)(1). (hogof)(1)= (Simplify your answer. Type an integer or a decimal.)arrow_forwardFor the given function, find (a) the equation of the secant line through the points where x has the given values and (b) the equation of the tangent line when x has the first value. y= f(x) = x²+x; x=-1,x=2 a. Which of the following formulas can be used to find the slope of the secant line? ○ A. 2-(-1) f(2) f(-1) 2+(-1) C. 1(2)+(-1) The equation of the secant line is 1(2)+(-1) О в. 2+(-1) f(2)-(-1) D. 2-(-1)arrow_forwardplease do not use chat gptarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
