Calculus: Early Transcendental Functions (MindTap Course List)
Calculus: Early Transcendental Functions (MindTap Course List)
6th Edition
ISBN: 9781285774770
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 15.7, Problem 1E

Verifying the Divergence TheoremIn Exercises 3–8, verify the Divergence Theorem by

Evaluating ∬ S F . N d S as a surface integral and as a triple integral

F ( x , y , z ) = 2 x i − 2 y j + z 2 k

S: cube bounded by the planes x = 0 , x = 1 , x = 0 , y = 0 , y = 1 , z = 0 , z = 1

Chapter 15.7, Problem 1E, Verifying the Divergence TheoremIn Exercises 38, verify the Divergence Theorem by Evaluating , example 1

Verifying the Divergence Theorem In Exercises 3–8, verify the Divergence Theorem by

Evaluating ∬ S F . N d S as a surface integral and as a triple integral

F ( x , y , z ) = 2 x i − 2 y j + z 2 k

S: cube bounded by the planes x = 0 , x = 1 , x = 0 , y = 0 , y = 1 , z = 0 , z = 1

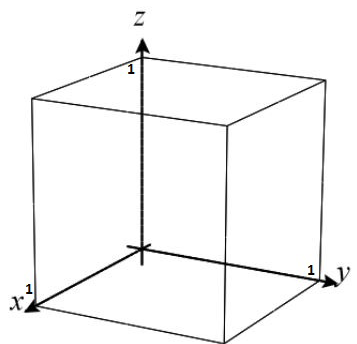
Chapter 15.7, Problem 1E, Verifying the Divergence TheoremIn Exercises 38, verify the Divergence Theorem by Evaluating , example 2

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 15.7, Problem 20E
Next
Chapter 15.7, Problem 2E
Students have asked these similar questions
Gauss's theorem or divergência theorem
Gauss's theorem or divergência theorem
Evaluate the circulation of G = xyi+zj+7yk around a square of side 9, centered at the origin, lying in the yz-plane, and oriented counterclockwise when viewed from the positive x-axis. Circulation = Prevs So F.dr-

Chapter 15 Solutions

Calculus: Early Transcendental Functions (MindTap Course List)

Ch. 15.1 - Vector Field Define a vector field in the plane...Ch. 15.1 - Prob. 66ECh. 15.1 - Prob. 1ECh. 15.1 - In Exercise 5-8, match the vector field with its...Ch. 15.1 - In Exercise 5-8, match the vector field with its...Ch. 15.1 - In Exercise 5-8, match the vector field with its...Ch. 15.1 - Prob. 5ECh. 15.1 - Prob. 6ECh. 15.1 - Prob. 7ECh. 15.1 - Prob. 8E
Ch. 15.1 - Sketching a Vector Field In Exercises 9-14, find F...Ch. 15.1 - Prob. 10ECh. 15.1 - Prob. 11ECh. 15.1 - Prob. 12ECh. 15.1 - Prob. 13ECh. 15.1 - Prob. 14ECh. 15.1 - Finding a Conservative Vector Field In Exercises...Ch. 15.1 - Prob. 16ECh. 15.1 - Prob. 17ECh. 15.1 - Prob. 18ECh. 15.1 - In Exercises 19-28, find the conservative vector...Ch. 15.1 - Prob. 20ECh. 15.1 - Prob. 21ECh. 15.1 - In Exercises 19-28, find the conservative vector...Ch. 15.1 - In Exercises 19-28, find the conservative vector...Ch. 15.1 - Prob. 24ECh. 15.1 - Prob. 25ECh. 15.1 - Prob. 26ECh. 15.1 - Prob. 27ECh. 15.1 - Prob. 28ECh. 15.1 - Prob. 29ECh. 15.1 - Prob. 30ECh. 15.1 - Prob. 31ECh. 15.1 - Prob. 32ECh. 15.1 - Prob. 33ECh. 15.1 - Prob. 34ECh. 15.1 - Prob. 35ECh. 15.1 - Prob. 36ECh. 15.1 - Prob. 37ECh. 15.1 - Prob. 38ECh. 15.1 - Prob. 39ECh. 15.1 - Prob. 40ECh. 15.1 - Prob. 41ECh. 15.1 - Prob. 42ECh. 15.1 - Find curl F for the vector field at the given...Ch. 15.1 - Find Curl F for the vector field at the point...Ch. 15.1 - Find Curl of the vector field F at the given point...Ch. 15.1 - Find Curl of the vector field F at the given point...Ch. 15.1 - Prob. 47ECh. 15.1 - Prob. 48ECh. 15.1 - Prob. 49ECh. 15.1 - Prob. 50ECh. 15.1 - Prob. 51ECh. 15.1 - Determine whether the vector field F is...Ch. 15.1 - Determine whether the vector field F is...Ch. 15.1 - Determine whether the vector field F is...Ch. 15.1 - Prob. 55ECh. 15.1 - Determine whether the vector field F is...Ch. 15.1 - Prob. 57ECh. 15.1 - Prob. 58ECh. 15.1 - Prob. 59ECh. 15.1 - Prob. 60ECh. 15.1 - Finding the Divergence of a Vector Field In...Ch. 15.1 - Find the divergence of the vector field at the...Ch. 15.1 - Prob. 63ECh. 15.1 - Prob. 64ECh. 15.1 - Prob. 78ECh. 15.1 - Prob. 67ECh. 15.1 - Prob. 68ECh. 15.1 - Prob. 69ECh. 15.1 - In Exercise 69 and 70, find curl (FxG)=x(FxG)...Ch. 15.1 - Prob. 71ECh. 15.1 - In Exercises 71 and 72, curl (curlF)=x(xF)...Ch. 15.1 - Prob. 73ECh. 15.1 - Divergence of a Cross Product In Exercises 73 and...Ch. 15.1 - Prob. 75ECh. 15.1 - Prob. 76ECh. 15.1 - In parts (a) - (h), prove the property for vector...Ch. 15.1 - Prob. 83ECh. 15.1 - Prob. 79ECh. 15.1 - Prob. 80ECh. 15.1 - Prob. 81ECh. 15.1 - Prob. 82ECh. 15.2 - Finding a Piecewise Smooth Parametrization In...Ch. 15.2 - Prob. 2ECh. 15.2 - Finding a Piecewise Smooth Parametrization In...Ch. 15.2 - Prob. 4ECh. 15.2 - Finding a Piecewise Smooth Parametrization In...Ch. 15.2 - Finding a Piecewise Smooth Parametrization In...Ch. 15.2 - Evaluating a Line Integral In Exercises 9-12, (a)...Ch. 15.2 - Evaluating a Line Integral In Exercises 9-12, (a)...Ch. 15.2 - Prob. 13ECh. 15.2 - Prob. 14ECh. 15.2 - Prob. 15ECh. 15.2 - Prob. 16ECh. 15.2 - Prob. 17ECh. 15.2 - Prob. 18ECh. 15.2 - Prob. 19ECh. 15.2 - Prob. 20ECh. 15.2 - Evaluating a Line Integral In Exercises 19-22,...Ch. 15.2 - Evaluating a Line Integral In Exercises 19-22,...Ch. 15.2 - Evaluating a Line Integral In Exercises 19-22,...Ch. 15.2 - Evaluating a Line Integral In Exercises 19-22,...Ch. 15.2 - Prob. 21ECh. 15.2 - Mass In Exercises 23 and 24, find the total mass...Ch. 15.2 - Prob. 23ECh. 15.2 - Prob. 24ECh. 15.2 - Prob. 25ECh. 15.2 - Mass In Exercises 25-28, find the total mass of...Ch. 15.2 - Prob. 27ECh. 15.2 - Evaluating a Line Integral of a Vector Field In...Ch. 15.2 - Prob. 29ECh. 15.2 - Prob. 30ECh. 15.2 - Prob. 31ECh. 15.2 - Evaluating a Line Integral of a Vector Field In...Ch. 15.2 - Prob. 33ECh. 15.2 - Prob. 34ECh. 15.2 - Prob. 35ECh. 15.2 - Work In Exercises 37-42, find the work done by the...Ch. 15.2 - Prob. 37ECh. 15.2 - Work In Exercises 37-42, find the work done by the...Ch. 15.2 - Prob. 39ECh. 15.2 - Work In Exercises 37-42, find the work done by the...Ch. 15.2 - Work In Exercises 43-46, determine whether the...Ch. 15.2 - Work In Exercises 43-46, determine whether the...Ch. 15.2 - Prob. 43ECh. 15.2 - Prob. 44ECh. 15.2 - Prob. 45ECh. 15.2 - Prob. 46ECh. 15.2 - Prob. 47ECh. 15.2 - Prob. 48ECh. 15.2 - Prob. 49ECh. 15.2 - Prob. 50ECh. 15.2 - Evaluating a Line Integral in Differential Form In...Ch. 15.2 - Prob. 52ECh. 15.2 - Prob. 53ECh. 15.2 - Prob. 54ECh. 15.2 - Evaluating a Line Integral in Differential Form In...Ch. 15.2 - Evaluating a Line Integral in Differential Form In...Ch. 15.2 - Prob. 57ECh. 15.2 - Prob. 58ECh. 15.2 - Prob. 59ECh. 15.2 - Evaluating a Line Integral in Differential Form In...Ch. 15.2 - Prob. 61ECh. 15.2 - Prob. 62ECh. 15.2 - Prob. 63ECh. 15.2 - Lateral Surface Area In Exercises 65-72, find the...Ch. 15.2 - Prob. 65ECh. 15.2 - Prob. 66ECh. 15.2 - Prob. 67ECh. 15.2 - Lateral Surface Area In Exercises 65-72, find the...Ch. 15.2 - Prob. 69ECh. 15.2 - Lateral Surface Area In Exercises 65-72, find the...Ch. 15.2 - Prob. 71ECh. 15.2 - Prob. 72ECh. 15.2 - Prob. 73ECh. 15.2 - Prob. 74ECh. 15.2 - Prob. 75ECh. 15.2 - Prob. 76ECh. 15.2 - Work Find the work done by a person weighing 175...Ch. 15.2 - Prob. 78ECh. 15.2 - Prob. 79ECh. 15.2 - Prob. 80ECh. 15.2 - Prob. 81ECh. 15.2 - Prob. 82ECh. 15.2 - Prob. 83ECh. 15.2 - Prob. 84ECh. 15.2 - Prob. 85ECh. 15.2 - Prob. 86ECh. 15.2 - Prob. 87ECh. 15.3 - Fundamental Theorem of Line integrals Explain how...Ch. 15.3 - Prob. 42ECh. 15.3 - In Exercises 9-18, evaluate CFdr using the...Ch. 15.3 - Prob. 26ECh. 15.3 - In Exercises 9-18, evaluate CFdr using the...Ch. 15.3 - Prob. 29ECh. 15.3 - Prob. 30ECh. 15.3 - Prob. 31ECh. 15.3 - Prob. 32ECh. 15.3 - In Exercises 9-18, evaluate CFdr using the...Ch. 15.3 - Prob. 34ECh. 15.3 - Prob. 35ECh. 15.3 - Prob. 36ECh. 15.3 - Prob. 11ECh. 15.3 - Evaluating a Line Integral In Exercises 23-32,...Ch. 15.3 - Evaluating a Line Integral In Exercises 23-32,...Ch. 15.3 - Evaluating a Line Integral In Exercises 23-32,...Ch. 15.3 - Prob. 19ECh. 15.3 - Evaluating a Line Integral In exercises 23-32,...Ch. 15.3 - Prob. 21ECh. 15.3 - Prob. 22ECh. 15.3 - Prob. 23ECh. 15.3 - Prob. 24ECh. 15.3 - Prob. 37ECh. 15.3 - Prob. 39ECh. 15.3 - Prob. 40ECh. 15.3 - Prob. 43ECh. 15.3 - Prob. 38ECh. 15.3 - Prob. 44ECh. 15.3 - Prob. 45ECh. 15.3 - Prob. 46ECh. 15.3 - Prob. 47ECh. 15.3 - Prob. 48ECh. 15.3 - Prob. 49ECh. 15.3 - Prob. 50ECh. 15.3 - Prob. 51ECh. 15.3 - Prob. 52ECh. 15.3 - Prob. 53ECh. 15.3 - Prob. 1ECh. 15.3 - Prob. 2ECh. 15.3 - Evaluating a Line Integral for Different...Ch. 15.3 - Evaluating a Line Integral for Different...Ch. 15.3 - Prob. 5ECh. 15.3 - Prob. 6ECh. 15.3 - Prob. 7ECh. 15.3 - Prob. 8ECh. 15.3 - Prob. 9ECh. 15.3 - Prob. 10ECh. 15.3 - Prob. 13ECh. 15.3 - Prob. 14ECh. 15.3 - Prob. 17ECh. 15.3 - Prob. 18ECh. 15.3 - Using the Fundamental Theorem of Line...Ch. 15.4 - Prob. 1ECh. 15.4 - Verifying Greens Theorem In Exercises 5-8, verify...Ch. 15.4 - Prob. 3ECh. 15.4 - Verifying Greens Theorem In Exercises 5-8, verify...Ch. 15.4 - Prob. 5ECh. 15.4 - Prob. 6ECh. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Prob. 11ECh. 15.4 - Prob. 12ECh. 15.4 - Prob. 13ECh. 15.4 - Prob. 14ECh. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Prob. 16ECh. 15.4 - Prob. 17ECh. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Evaluating a Line Integral Using Greens Theorem In...Ch. 15.4 - Work In Exercises 25-28, use Greens Theorem to...Ch. 15.4 - Prob. 22ECh. 15.4 - Prob. 23ECh. 15.4 - Work In Exercises 25-28, use Greens Theorem to...Ch. 15.4 - Prob. 25ECh. 15.4 - Prob. 26ECh. 15.4 - Prob. 27ECh. 15.4 - Prob. 28ECh. 15.4 - Prob. 29ECh. 15.4 - Prob. 30ECh. 15.4 - Prob. 31ECh. 15.4 - Using Greens Theorem to Verify a Formula In...Ch. 15.4 - Centroid In Exercises 35-38, use the results of...Ch. 15.4 - Prob. 34ECh. 15.4 - Prob. 35ECh. 15.4 - Prob. 36ECh. 15.4 - Prob. 37ECh. 15.4 - Area In Exercises 39-42, use the result of...Ch. 15.4 - Area In Exercises 39-42, use the result of...Ch. 15.4 - Area In Exercises 39-42, use the result of...Ch. 15.4 - Prob. 41ECh. 15.4 - Prob. 42ECh. 15.4 - Greens Theorem: Region with a Hole Let R be the...Ch. 15.4 - Greens Theorem: Region with a Hole Let R be the...Ch. 15.4 - Prob. 45ECh. 15.4 - Prob. 46ECh. 15.4 - Prob. 47ECh. 15.4 - Prob. 48ECh. 15.4 - Prob. 49ECh. 15.4 - Proof In Exercises 51 and 52, prove the identity,...Ch. 15.4 - Prob. 51ECh. 15.4 - Prob. 52ECh. 15.5 - Matching In Exercises 3-8, match the vector-valued...Ch. 15.5 - Prob. 2ECh. 15.5 - Prob. 3ECh. 15.5 - Matching In Exercises 16, match the vector-valued...Ch. 15.5 - Prob. 5ECh. 15.5 - Prob. 6ECh. 15.5 - Prob. 7ECh. 15.5 - Prob. 8ECh. 15.5 - Prob. 9ECh. 15.5 - Prob. 10ECh. 15.5 - Prob. 11ECh. 15.5 - Prob. 12ECh. 15.5 - Prob. 13ECh. 15.5 - Prob. 14ECh. 15.5 - Graphing a Parametric Surface In Exercises 13-16,...Ch. 15.5 - Prob. 16ECh. 15.5 - Prob. 21ECh. 15.5 - Prob. 22ECh. 15.5 - Prob. 23ECh. 15.5 - Prob. 24ECh. 15.5 - Prob. 25ECh. 15.5 - Prob. 26ECh. 15.5 - Prob. 27ECh. 15.5 - Prob. 28ECh. 15.5 - Prob. 29ECh. 15.5 - Representing a Surface Parametrically In Exercises...Ch. 15.5 - Prob. 31ECh. 15.5 - Prob. 32ECh. 15.5 - Prob. 33ECh. 15.5 - Prob. 34ECh. 15.5 - Prob. 35ECh. 15.5 - Prob. 36ECh. 15.5 - Prob. 37ECh. 15.5 - Prob. 38ECh. 15.5 - Prob. 39ECh. 15.5 - Prob. 40ECh. 15.5 - Prob. 41ECh. 15.5 - Prob. 42ECh. 15.5 - Prob. 43ECh. 15.5 - Prob. 44ECh. 15.5 - Prob. 45ECh. 15.5 - Prob. 46ECh. 15.5 - Prob. 17ECh. 15.5 - Prob. 18ECh. 15.5 - Prob. 19ECh. 15.5 - Prob. 20ECh. 15.5 - Prob. 47ECh. 15.5 - Prob. 48ECh. 15.5 - Prob. 49ECh. 15.5 - Prob. 50ECh. 15.5 - Prob. 51ECh. 15.5 - Prob. 52ECh. 15.5 - Prob. 53ECh. 15.5 - Prob. 54ECh. 15.5 - Prob. 55ECh. 15.5 - Hyperboloid Find a vector-valued function for the...Ch. 15.5 - Prob. 57ECh. 15.5 - Prob. 58ECh. 15.5 - Prob. 59ECh. 15.5 - Prob. 60ECh. 15.6 - Prob. 1ECh. 15.6 - Prob. 2ECh. 15.6 - Prob. 3ECh. 15.6 - Prob. 4ECh. 15.6 - Prob. 5ECh. 15.6 - Prob. 6ECh. 15.6 - Evaluating a Surface Integral In Exercises 7 and...Ch. 15.6 - Prob. 8ECh. 15.6 - Prob. 9ECh. 15.6 - Prob. 10ECh. 15.6 - Prob. 11ECh. 15.6 - Mass In Exercise 13-14, find the mass of the...Ch. 15.6 - Prob. 13ECh. 15.6 - Prob. 14ECh. 15.6 - Prob. 15ECh. 15.6 - Prob. 16ECh. 15.6 - Prob. 17ECh. 15.6 - Evaluating a Surface Integral In Exercises 19-24,...Ch. 15.6 - Prob. 19ECh. 15.6 - Evaluating a Surface Integral In Exercises 19-24,...Ch. 15.6 - Evaluating a Surface Integral In Exercises 19-24,...Ch. 15.6 - Prob. 22ECh. 15.6 - Prob. 23ECh. 15.6 - Prob. 24ECh. 15.6 - Evaluating a Flux Integral In Exercises 25-30,...Ch. 15.6 - Prob. 26ECh. 15.6 - Prob. 27ECh. 15.6 - Evaluating a Flux Integral In Exercises 25-30,...Ch. 15.6 - Prob. 29ECh. 15.6 - Prob. 30ECh. 15.6 - Prob. 37ECh. 15.6 - Prob. 38ECh. 15.6 - Prob. 31ECh. 15.6 - Electrical Charge Let E=xi+yj+2zk be an...Ch. 15.6 - Prob. 33ECh. 15.6 - Moments of Inertia In Exercises 37-40, use the...Ch. 15.6 - Prob. 35ECh. 15.6 - Prob. 36ECh. 15.6 - Prob. 39ECh. 15.6 - Prob. 40ECh. 15.6 - Prob. 41ECh. 15.6 - Prob. 42ECh. 15.6 - Prob. 43ECh. 15.7 - Classifying a Point in a Vector Field How do you...Ch. 15.7 - Verifying the Divergence TheoremIn Exercises 38,...Ch. 15.7 - Verifying the Divergence Theorem In Exercises 3-8,...Ch. 15.7 - Verifying the Divergence Theorem In Exercises 3-8,...Ch. 15.7 - Verifying the Divergence Theorem In Exercises 3-8,...Ch. 15.7 - Prob. 5ECh. 15.7 - Verifying the Divergence Theorem In Exercises 3-8,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Prob. 11ECh. 15.7 - Prob. 12ECh. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Using the Divergence Theorem In Exercises 9-18,...Ch. 15.7 - Prob. 17ECh. 15.7 - Prob. 18ECh. 15.7 - WRITING ABOUT CONCEPTS Divergence Theorem State...Ch. 15.7 - EXPLORING CONCEPTS Closed Surface What is the...Ch. 15.7 - Prob. 22ECh. 15.7 - Prob. 23ECh. 15.7 - Prob. 24ECh. 15.7 - Prob. 25ECh. 15.7 - Prob. 26ECh. 15.7 - Prob. 27ECh. 15.7 - Prob. 28ECh. 15.8 - Prob. 22ECh. 15.8 - Prob. 1ECh. 15.8 - Prob. 2ECh. 15.8 - Prob. 3ECh. 15.8 - Prob. 4ECh. 15.8 - Prob. 5ECh. 15.8 - Verifying Stokess Theorem In Exercises 3-6, verify...Ch. 15.8 - Verifying Stokess Theorem In Exercises 3-6, verify...Ch. 15.8 - Verifying Stokes Theorem In Exercises 3-6, verify...Ch. 15.8 - Using Stokess Theorem In Exercises 7-16, use...Ch. 15.8 - Using Stokess Theorem In Exercises 918, use...Ch. 15.8 - Using Stokess Theorem In Exercises 7-16, use...Ch. 15.8 - Prob. 12ECh. 15.8 - Prob. 13ECh. 15.8 - Using Stokess Theorem In Exercises 7-16, use...Ch. 15.8 - Using Stokess Theorem In Exercises 7-16, use...Ch. 15.8 - Prob. 16ECh. 15.8 - Prob. 17ECh. 15.8 - Prob. 18ECh. 15.8 - Prob. 19ECh. 15.8 - Prob. 20ECh. 15.8 - Prob. 21ECh. 15.8 - Prob. 23ECh. 15.8 - Prob. 24ECh. 15.8 - Prob. 25ECh. 15 - Sketching a Vector Field In Exercises 1 and 2,...Ch. 15 - Sketching a Vector Field In Exercises 1 and 2,...Ch. 15 - Prob. 3RECh. 15 - Prob. 4RECh. 15 - Prob. 5RECh. 15 - Prob. 6RECh. 15 - Prob. 7RECh. 15 - Prob. 8RECh. 15 - Prob. 9RECh. 15 - Prob. 10RECh. 15 - Prob. 11RECh. 15 - Prob. 12RECh. 15 - Prob. 13RECh. 15 - Prob. 14RECh. 15 - Prob. 15RECh. 15 - Prob. 16RECh. 15 - Prob. 17RECh. 15 - Prob. 18RECh. 15 - Prob. 19RECh. 15 - Prob. 20RECh. 15 - Prob. 21RECh. 15 - Prob. 22RECh. 15 - Prob. 23RECh. 15 - Prob. 24RECh. 15 - Evaluating a Line IntegralIn Exercises 2126,...Ch. 15 - Prob. 26RECh. 15 - Prob. 27RECh. 15 - Prob. 28RECh. 15 - Prob. 29RECh. 15 - Lateral Surface Area In Exercises 43 and44, find...Ch. 15 - Prob. 31RECh. 15 - Prob. 32RECh. 15 - Prob. 33RECh. 15 - Evaluating a Line Integral of a Vector Field In...Ch. 15 - Prob. 35RECh. 15 - Prob. 36RECh. 15 - Prob. 37RECh. 15 - Prob. 38RECh. 15 - Prob. 39RECh. 15 - Prob. 40RECh. 15 - Using the Fundamental Theorem of line Integrals In...Ch. 15 - Prob. 42RECh. 15 - Prob. 43RECh. 15 - Prob. 44RECh. 15 - Prob. 45RECh. 15 - Prob. 46RECh. 15 - Prob. 47RECh. 15 - Prob. 48RECh. 15 - Prob. 49RECh. 15 - Prob. 50RECh. 15 - Prob. 51RECh. 15 - Prob. 52RECh. 15 - Prob. 53RECh. 15 - Prob. 54RECh. 15 - Prob. 55RECh. 15 - Mass A cone-shaped surface lamina S is given by...Ch. 15 - Prob. 57RECh. 15 - Prob. 58RECh. 15 - Using Stokess Theorem In Exercises 83 and 84, use...Ch. 15 - Prob. 60RECh. 15 - Prob. 61RECh. 15 - Heat Flux Consider a single heat source located at...Ch. 15 - Prob. 2PSCh. 15 - Prob. 3PSCh. 15 - Moments of Inertia Find the moments of inertia for...Ch. 15 - Prob. 5PSCh. 15 - Prob. 6PSCh. 15 - Prob. 7PSCh. 15 - Prob. 8PSCh. 15 - Prob. 9PSCh. 15 - Prob. 10PSCh. 15 - Proof Let S be a smooth oriented surface with...Ch. 15 - Area and Work How does the area of the ellipse...Ch. 15 - Prob. 13PS
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY