CENGAGENOW FOR ANDERSON/SWEENEY/WILLIAM
13th Edition
ISBN: 9781337094399
Author: Cochran
Publisher: IACCENGAGE
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 15, Problem 51SE
A partial computer output from a
Analysis of Variance
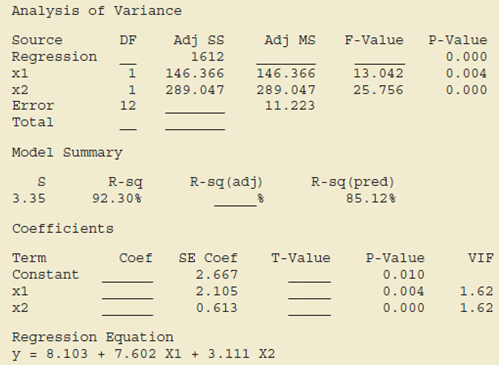
Regression Equation
y = 8.103 + 7.602 X1 + 3.111 X2
- a. Compute the missing entries in this output.
- b. Use the F test and α = .05 to see whether a significant relationship is present.
- c. Use the t test and α = .05 to test H0: β1 = 0 and H0: β2 = 0.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Use the shoe print lengths and heights shown below to find the regression equation, letting shoe print lengths be the predictor (x) variable. Then find the best predicted height of a male who has a shoe print length of
28.5
cm. Would the result be helpful to police crime scene investigators in trying to describe the male? Use a significance level of
α=0.05.
Shoe Print (cm)
29.1
29.1
31.8
31.9
27.5
Foot Length (cm)
25.7
25.4
27.9
26.7
25.1
Height (cm)
175.4
177.8
185.2
175.4
173.2
The best predicted height is
enter your response here
cm.
(Round to two decimal places as needed.)
Would the result be helpful?
A.
No, because the description would be the same regardless of shoe print length.
B.
Yes, because the description would be based on an actual shoe print length.
C.
Yes, because the correlation is strong, so the predicted…
Help with:
Draw a scatter diagram of the data, treating age as the explanatory variable. What type of relation, if any, appears to exist between age and HDL cholesterol?
Determine the least-squares regression equation from the sample data
Assuming the residuals are normally distributed, test whether a linear relation exists between age and HDL cholesterol levels at the α=0.01 level of significance.
What are the null and alternative hypotheses?
What is the P Value:
What conclusion can be drawn at α=0.01 level of significance?
Assuming the residuals are normally distributed, construct a 95% confidence interval about the slope of the true least-squares regression line.
Lower bound
Upper bound
For a 42-year-old male patient who visits the doctor's office, would using the least-squares regression line obtained in part (b) to predict the HDL cholesterol of this patient be recommended?
A good estimate for the HDL cholesterol of this patient is
Write down the estimated regression equation.
What is the value of R square in this regression model? Compared with the R-square in Question 1, what is the additional contribution of gender to the percentage of variance explained?
Interpret the meaning of the regression coefficient of Year in College (how does year in college affect salary?). Does this variable have a significant impact on income level at α= .05? How does one more year in college affect salary if the gender is the same? How do you get this conclusion?
Chapter 15 Solutions
CENGAGENOW FOR ANDERSON/SWEENEY/WILLIAM
Ch. 15.2 - The estimated regression equation for a model...Ch. 15.2 - Consider the following data for a dependent...Ch. 15.2 - In a regression analysis involving 30...Ch. 15.2 - A shoe store developed the following estimated...Ch. 15.2 - The owner of Showtime Movie Theaters, Inc., would...Ch. 15.2 - The National Football League (NFL) records a...Ch. 15.2 - PC Magazine provided ratings for several...Ch. 15.2 - The Cond Nast Traveler Gold List provides ratings...Ch. 15.2 - The Professional Golfers Association (PGA)...Ch. 15.2 - Prob. 10E
Ch. 15.3 - In exercise 1, the following estimated regression...Ch. 15.3 - Prob. 12ECh. 15.3 - In exercise 3, the following estimated regression...Ch. 15.3 - In exercise 4, the following estimated regression...Ch. 15.3 - In exercise 5, the owner of Showtime Movie...Ch. 15.3 - In exercise 6, data were given on the average...Ch. 15.3 - Prob. 17ECh. 15.3 - Refer to exercise 10, where Major League Baseball...Ch. 15.5 - In exercise 1, the following estimated regression...Ch. 15.5 - Refer to the data presented in exercise 2. The...Ch. 15.5 - The following estimated regression equation was...Ch. 15.5 - In exercise 4, the following estimated regression...Ch. 15.5 - Prob. 23ECh. 15.5 - Prob. 24ECh. 15.5 - The Cond Nast Traveler Gold List for 2012 provided...Ch. 15.5 - In exercise 10, data showing the values of several...Ch. 15.6 - In exercise 1, the following estimated regression...Ch. 15.6 - Refer to the data in exercise 2. The estimated...Ch. 15.6 - In exercise 5, the owner of Showtime Movie...Ch. 15.6 - In exercise 24, an estimated regression equation...Ch. 15.6 - The American Association of Individual Investors...Ch. 15.7 - Consider a regression study involving a dependent...Ch. 15.7 - Consider a regression study involving a dependent...Ch. 15.7 - Management proposed the following regression model...Ch. 15.7 - Refer to the Johnson Filtration problem introduced...Ch. 15.7 - This problem is an extension of the situation...Ch. 15.7 - The Consumer Reports Restaurant Customer...Ch. 15.7 - A 10-year study conducted by the American Heart...Ch. 15.8 - Data for two variables, x and y, follow. xi 1 2 3...Ch. 15.8 - Data for two variables, x and y, follow. xi 22 24...Ch. 15.8 - Exercise 5 gave the following data on weekly gross...Ch. 15.8 - The following data show the curb weight,...Ch. 15.8 - The Ladies Professional Golfers Association (LPGA)...Ch. 15.9 - Refer to the Simmons Stores example introduced in...Ch. 15.9 - In Table 15.12 we provided estimates of the...Ch. 15.9 - Community Bank would like to increase the number...Ch. 15.9 - Over the past few years the percentage of students...Ch. 15.9 - The Tire Rack maintains an independent consumer...Ch. 15 - The admissions officer for Clearwater College...Ch. 15 - The personnel director for Electronics Associates...Ch. 15 - A partial computer output from a regression...Ch. 15 - Recall that in exercise 49, the admissions officer...Ch. 15 - Recall that in exercise 50 the personnel director...Ch. 15 - The Tire Rack, Americas leading online distributor...Ch. 15 - The Department of Energy and the U.S....Ch. 15 - A portion of a data set containing information for...Ch. 15 - Fortune magazine publishes an annual list of the...Ch. 15 - Consumer Research, Inc., is an independent agency...Ch. 15 - Matt Kenseth won the 2012 Daytona 500, the most...Ch. 15 - Finding the Best Car Value When trying to decide...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Find the equation of the regression line for the following data set. x 1 2 3 y 0 3 4arrow_forwardLife Expectancy The following table shows the average life expectancy, in years, of a child born in the given year42 Life expectancy 2005 77.6 2007 78.1 2009 78.5 2011 78.7 2013 78.8 a. Find the equation of the regression line, and explain the meaning of its slope. b. Plot the data points and the regression line. c. Explain in practical terms the meaning of the slope of the regression line. d. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 2019? e. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 1580?2300arrow_forwardOlympic Pole Vault The graph in Figure 7 indicates that in recent years the winning Olympic men’s pole vault height has fallen below the value predicted by the regression line in Example 2. This might have occurred because when the pole vault was a new event there was much room for improvement in vaulters’ performances, whereas now even the best training can produce only incremental advances. Let’s see whether concentrating on more recent results gives a better predictor of future records. (a) Use the data in Table 2 (page 176) to complete the table of winning pole vault heights shown in the margin. (Note that we are using x=0 to correspond to the year 1972, where this restricted data set begins.) (b) Find the regression line for the data in part ‚(a). (c) Plot the data and the regression line on the same axes. Does the regression line seem to provide a good model for the data? (d) What does the regression line predict as the winning pole vault height for the 2012 Olympics? Compare this predicted value to the actual 2012 winning height of 5.97 m, as described on page 177. Has this new regression line provided a better prediction than the line in Example 2?arrow_forward
- For the following exercises, use Table 4 which shows the percent of unemployed persons 25 years or older who are college graduates in a particular city, by year. Based on the set of data given in Table 5, calculate the regression line using a calculator or other technology tool, and determine the correlation coefficient. Round to three decimal places of accuracyarrow_forwardXYZ Corporation Stock Prices The following table shows the average stock price, in dollars, of XYZ Corporation in the given month. Month Stock price January 2011 43.71 February 2011 44.22 March 2011 44.44 April 2011 45.17 May 2011 45.97 a. Find the equation of the regression line. Round the regression coefficients to three decimal places. b. Plot the data points and the regression line. c. Explain in practical terms the meaning of the slope of the regression line. d. Based on the trend of the regression line, what do you predict the stock price to be in January 2012? January 2013?arrow_forwardNoise and Intelligibility Audiologists study the intelligibility of spoken sentences under different noise levels. Intelligibility, the MRT score, is measured as the percent of a spoken sentence that the listener can decipher at a cesl4ain noise level in decibels (dB). The table shows the results of one such test. (a) Make a scatter plot of the data. (b) Find and graph the regression line. (c) Find the correlation coefficient. Is a linear model appropriate? (d) Use the linear model in put (b) to estimate the intelligibility of a sentence at a 94-dB noise level.arrow_forward
- Determine if the statement is true or false.arrow_forwardA regression was run to determine if there is a relationship between the happiness index (y) and life expectancy in years of a given country (x). The results of the regression were: ý=a+bx a=-1.692 b=0.117 (a) Write the equation of the Least Squares Regression line of the form (b) Which is a possible value for the correlation coefficient, r? O -0.649 O 1.32 O 0.649 O-1.32 (c) If a country increases its life expectancy, the happiness index will O increase O decrease (d) If the life expectancy is increased by 2.5 years in a certain country, how much will the happiness index change? Round to two decimal places. (e) Use the regression line to predict the happiness index of a country with a life expectancy of 75 years. Round to two decimal places.arrow_forwardThe fish in my pond have mean length 12 inches and mean weight 5 pounds. The correlation coefficient of length and weight is .8. If the length of a particular randomly selected fish is reported to be 12 inches, then what should we predict for the weight of that fish using simple linear regression?arrow_forward
- a ift = The table below gives the age and bone density for five randomly selected women. Using this data, consider the equation of the regression line, bo + b₁x, for predicting a woman's bone density based on her age. Keep in mind, the correlation coefficient may or may not be statistically significant for the data given. Remember, In practice, it would not be appropriate to use the regression line to make a prediction if the correlation coefficient is not statistically significant. tab ** Answer How to enter your answer (opens in new window) Step 2 of 6: Find the estimated y-Intercept. Round your answer to three decimal places. esc 1945 ! 1 q alt a Z ebook x360 ng from any angle. @ 2 W S →>> X # 3 e d C $ 4 C r f Age Bone Density 359 % 5 V t g 36 51 63 66 70 357 328 314 310 Oll A 6 b y hp h & 7 O n u j * 8 N O i m ( 9 k O 100- 4 Tables ctrl { [ Keypad Keyboard Shortcuts Previous step answers Submit Answer D + = 11 : 90 ; ? Copy Data O SEAR Dec 2 Table ] USE YOUR SMARTPHONE FOR…arrow_forwardA regression was run to determine if there is a relationship between the happiness index (y) and life expectancy in years of a given country (x). The results of the regression were: ý=a+bx a=0.137 b=0.082 (a) Write the equation of the Least Squares Regression line of the form (b) Which is a possible value for the correlation coefficient, r? O-1.338 O-0.84 O 1.338 O 0.84 (c) If a country increases its life expectancy, the happiness index will O increase O decreasearrow_forwardUse the pizza cost and the subway fare in the table below to find the regression equation, letting pizza cost be the predictor (x) variable. (Pizza cost is in dollars per slice, subway fare and CPI are in dollars.) What is the best predicted subway fare when pizza costs $3.96 per slice? Use a significance level of 0.05. Year Pizza Cost Subway Fare CPI 1960 1973 1986 1995 2002 2003 2009 2013 2015 2019 0.151 0.350 1.000 1.249 1.753 2.001 2.247 2.304 2.747 2.999 0.152 0.349 0.998 1.351 1.503 2.003 2.250 2.551 2.752 2.746 29.6 44.4 109.6 152.4 180.0 184.0 214.5 233.0 237.0 252.2 The regression equation is ŷ = + (x. (Round the y-intercept to four decimal places as needed. Round the slope to three decimal places as needed.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License