
Concept explainers
Exercises 1 through 4 refer to the data set shown in Table 15-12. The table shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
Chem 103 test scores.
Table 15-12
Chem 103 test scores
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
a. Make a frequency table for the Chem 103 test scores.
b. Draw a bar graph for the data in Table 15-12.
a.
To find:
The frequency table for the Chem 103 test scores.
Answer to Problem 1E
Solution:
The frequency table for the Chem 103 test scores is given by,
| Score | Frequency |
| 10 | 1 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 100 | 2 |
Explanation of Solution
Given:
The table below shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
A frequency table is a table with the frequency of each actual value in the data set.
Approach:
From the given table the number of students with a score of 10 is 1, so the frequency of score 10 is 1, similarly the number of students with a score of 40 is 1, so the frequency of score 40 is 1 similarly frequencies for rest of scores can be computed.
The frequency table for the Chem 103 test is given by,
| Score | Frequency |
| 10 | 1 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 100 | 2 |
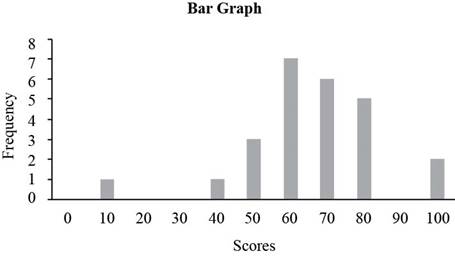
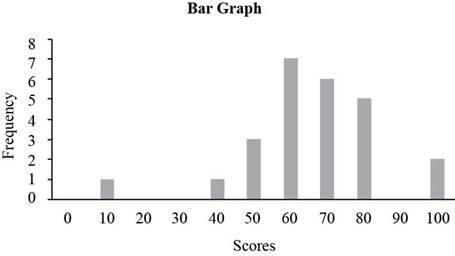
b)
To construct:
The bar graph corresponding to the given table.
Answer to Problem 1E
Solution:
The bar graph is given below.
Explanation of Solution
Given:
The table below shows the scores on a Chem 103 test consisting of 10 questions worth 10 points each.
| Student ID | Score | Student ID | Score |
| 1362 | 50 | 4315 | 70 |
| 1486 | 70 | 4719 | 70 |
| 1721 | 80 | 4951 | 60 |
| 1932 | 60 | 5321 | 60 |
| 2489 | 70 | 5872 | 100 |
| 2766 | 10 | 6433 | 50 |
| 2877 | 80 | 6921 | 50 |
| 2964 | 60 | 8317 | 70 |
| 3217 | 70 | 8854 | 100 |
| 3588 | 80 | 8964 | 80 |
| 3780 | 80 | 9158 | 60 |
| 3921 | 60 | 9347 | 60 |
| 4107 | 40 |
A bar graph is a graph with bars (column) representing each of the actual values in the data set. The height of each column represents the frequency of the value in the data set.
Approach:
From the given table the number of students with a score of 0 is 0, so the frequency of score 0 is 0, similarly the number of students with a score of 10 is 1, so the frequency of score 10 is 1 similarly frequencies for rest of scores can be computed.
The frequency table for the Chem 103 test is given by,
| Score | Frequency |
| 0 | 0 |
| 10 | 1 |
| 20 | 0 |
| 30 | 0 |
| 40 | 1 |
| 50 | 3 |
| 60 | 7 |
| 70 | 6 |
| 80 | 5 |
| 90 | 0 |
| 100 | 2 |
Place the scores along horizontal axis and the frequencies along vertical axis to construct bar graph. The bar graph of the frequency table is given below.
Want to see more full solutions like this?
Chapter 15 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Introductory Statistics
Elementary & Intermediate Algebra
Algebra and Trigonometry (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
- Refer to page 311 for a sequence of functions defined on a given interval. Instructions: • Analyze whether the sequence converges pointwise and/or uniformly on the given interval. • Discuss the implications of uniform convergence for integration and differentiation of the sequence. • Provide counterexamples if any condition fails. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 310 for a matrix and its associated system of differential equations. Instructions: • Find the eigenvalues of the given matrix and classify the stability of the system (e.g., stable, • unstable, saddle point). Discuss the geometric interpretation of eigenvalues in the context of system behavior. • Provide conditions under which the system exhibits periodic solutions. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 313 for a nonlinear differential equation and its linear approximation. Instructions: • Linearize the given nonlinear system around the equilibrium points. • Analyze the stability of each equilibrium using the Jacobian matrix and its eigenvalues. • Discuss the limitations of linearization for determining global behavior. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 314 for a matrix and its decomposed form. Instructions: • Verify the given singular value decomposition of the matrix. • • Discuss the geometric interpretation of the left and right singular vectors. Use the SVD to analyze the matrix's rank and nullity. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZ F/view?usp=sharing]arrow_forwardRefer to page 312 for a set of mappings between two groups G and H. Instructions: • • Verify which of the provided mappings are homomorphisms. Determine the kernel and image of valid homomorphisms and discuss their properties. • State whether the groups are isomorphic, justifying your conclusion. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward12:25 AM Sun Dec 22 uestion 6- Week 8: QuX Assume that a company X + → C ezto.mheducation.com Week 8: Quiz i Saved 6 4 points Help Save & Exit Submit Assume that a company is considering purchasing a machine for $50,000 that will have a five-year useful life and a $5,000 salvage value. The machine will lower operating costs by $17,000 per year. The company's required rate of return is 15%. The net present value of this investment is closest to: Click here to view Exhibit 12B-1 and Exhibit 12B-2, to determine the appropriate discount factor(s) using the tables provided. 00:33:45 Multiple Choice О $6,984. $11,859. $22,919. ○ $9,469, Mc Graw Hill 2 100-arrow_forward
- No chatgpt pls will upvotearrow_forward7. [10 marks] Let G = (V,E) be a 3-connected graph. We prove that for every x, y, z Є V, there is a cycle in G on which x, y, and z all lie. (a) First prove that there are two internally disjoint xy-paths Po and P₁. (b) If z is on either Po or P₁, then combining Po and P₁ produces a cycle on which x, y, and z all lie. So assume that z is not on Po and not on P₁. Now prove that there are three paths Qo, Q1, and Q2 such that: ⚫each Qi starts at z; • each Qi ends at a vertex w; that is on Po or on P₁, where wo, w₁, and w₂ are distinct; the paths Qo, Q1, Q2 are disjoint from each other (except at the start vertex 2) and are disjoint from the paths Po and P₁ (except at the end vertices wo, W1, and w₂). (c) Use paths Po, P₁, Qo, Q1, and Q2 to prove that there is a cycle on which x, y, and z all lie. (To do this, notice that two of the w; must be on the same Pj.)arrow_forward6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward
- 4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forwardQ/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt



