
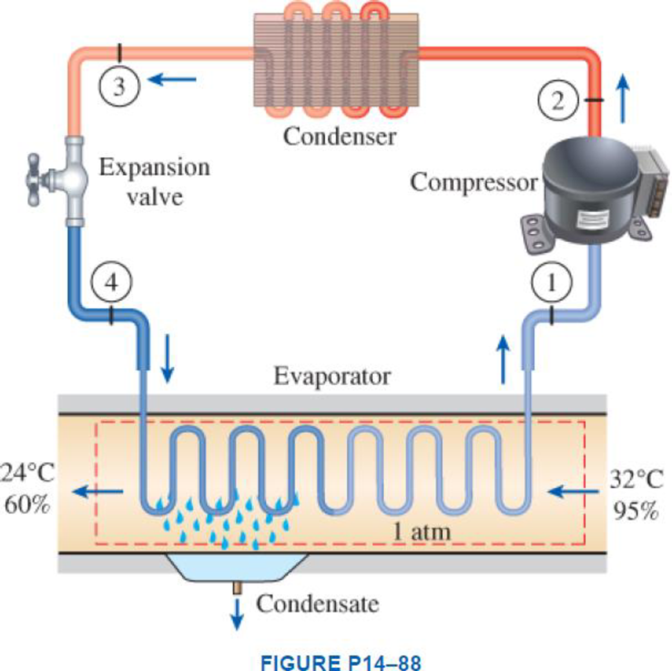
Atmospheric air at 1 atm, 32°C, and 95 percent relative humidity is cooled to 24°C and 60 percent relative humidity. A simple ideal vapor-compression refrigeration system using refrigerant-134a as the working fluid is used to provide the cooling required. It operates its evaporator at 4°C and its condenser at a saturation temperature of 39.4°C. The condenser rejects its heat to the atmospheric air. Calculate the exergy destruction, in kJ, in the total system per 1000 m3 of dry air processed.
The exergy destruction in the total system per
Answer to Problem 88P
The exergy destruction in the total system per
Explanation of Solution
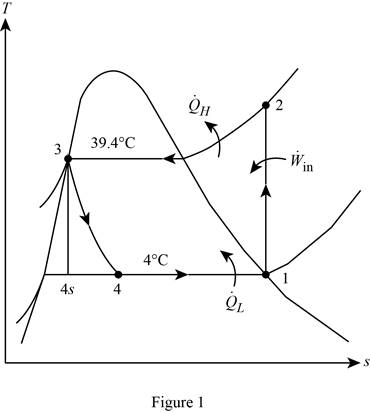
Show the T-s diagram for the simple ideal vapour-compression refrigeration system.
Express the mass of air.
Here, volume at state 1 is
Express the water mass balance and energy balance equations to the combined cooling and dehumidification section.
For water mass balance:
For energy balance:
Write the energy balance equation using steady-flow equation.
Here, the rate of total energy entering the system is
Substitute
Here, the specific enthalpy at the state 1 and 2 are
Write the formula for mass flow rate of refrigerant-134a.
Write the formula for amount of heat rejected from the condenser.
Calculate the exergy destruction in the components of the refrigeration cycle.
For the process 1-2,
Here, the process 1-2 is an isentropic.
For the process 2-3,
For the process 3-4,
Write the entropy change of water vapour in the air stream.
Write the entropy of water leaving the cooling section.
Determine the partial pressure of water vapour at state 1 for air steam.
Determine the partial pressure of dry air at state 1 for air steam.
Here, the pressure at the state 1 is
Determine the partial pressure of water vapour at state 2 for air steam.
Determine the partial pressure of dry air at state 2 for air steam.
Here, the pressure at the state 2 is
Write the formula for entropy change of dry air.
Write the formula for entropy change R-134a in the evaporator.
Write the formula for an entropy balance on the evaporator.
Write the formula for an exergy destruction in the evaporator.
Write the formula for the total exergy destruction.
Conclusion:
Refer Figure A-31, “psychometric chart at
Refer Table A-4, “saturated water-temperature table”, and write the specific enthalpy of condensate water at temperature of
Here, entropy of saturation liquid at temperature of
Write the formula of interpolation method of two variables.
Here, the variables denote by x and y is temperature and specific enthalpy of condensate water at state 2 respectively.
Show the specific enthalpy of condensate water at corresponding to temperature as in Table (1).
|
Temperature |
Specific enthalpy of condensate water |
| 25 | 104.83 |
| 28 | |
| 30 | 125.74 |
Substitute
Substitute
Substitute
Substitute 1105 kg for
Substitute 1105 kg for
From the Table A-11 “Saturated Refrigerant-134a-Pressure Table”, obtain the value of the specific enthalpy and entropy at state 1 of
Refer Table A-13 “Saturated Refrigerant-134a-Pressure Table”, and write the specific enthalpy at state 2 in 1 MPa of pressure and entropy of
From the Table A-12 “Saturated Refrigerant-134a-Pressure Table”, obtain the value of the specific enthalpy and entropy at state 3 of
Here, the specific enthalpy at the state 4 and 3 are equal in the throttling.
Calculate the value of
From the Table A-11 “Saturated Refrigerant-134a-Pressure Table”, obtain the value of the specific enthalpy and entropy of saturated liquid and change upon vaporization at state 4 of
Substitute
Calculate the value of specific entropy of the state 4.
Substitute
Substitute
Substitute
Substitute
Substitute
Refer Table A-4 “Saturated water-temperature Table”, and write the specific entropy at state 1 at
Refer Table A-4 “Saturated water-temperature Table”, and write the specific entropy at state 1 at
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute 0 for
Thus, the exergy destruction in the total system per
Want to see more full solutions like this?
Chapter 14 Solutions
CONNECT FOR THERMODYNAMICS: AN ENGINEERI
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD. The cantilevered spandrel beam shown whose depth tapers from d1 to d2, has a constant width of 120mm. It carries a triangularly distributed end reaction.Given: d1 = 600 mm, d2 = 120 mm, L = 1 m, w = 100 kN/m1. Calculate the maximum flexural stress at the support, in kN-m.2. Determine the distance (m), from the free end, of the section with maximum flexural stress.3. Determine the maximum flexural stress in the beam, in MPa.ANSWERS: (1) 4.630 MPa; (2) 905.8688 m; (3) 4.65 MPaarrow_forwardCORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD A concrete wall retains water as shown. Assume that the wall is fixed at the base. Given: H = 3 m, t = 0.5m, Concrete unit weight = 23 kN/m3Unit weight of water = 9.81 kN/m3(Hint: The pressure of water is linearly increasing from the surface to the bottom with intensity 9.81d.)1. Find the maximum compressive stress (MPa) at the base of the wall if the water reaches the top.2. If the maximum compressive stress at the base of the wall is not to exceed 0.40 MPa, what is the maximum allowable depth(m) of the water?3. If the tensile stress at the base is zero, what is the maximum allowable depth (m) of the water?ANSWERS: (1) 1.13 MPa, (2) 2.0 m, (3) 1.20 marrow_forwardCORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I NEED FBD A short plate is attached to the center of the shaft as shown. The bottom of the shaft is fixed to the ground.Given: a = 75 mm, h = 125 mm, D = 38 mmP1 = 24 kN, P2 = 28 kN1. Calculate the maximum torsional stress in the shaft, in MPa.2. Calculate the maximum flexural stress in the shaft, in MPa.3. Calculate the maximum horizontal shear stress in the shaft, in MPa.ANSWERS: (1) 167.07 MPa; (2) 679.77 MPa; (3) 28.22 MPaarrow_forward
- CORRECT AND DETAILED SOLUTION WITH FBD ONLY. I WILL UPVOTE THANK YOU. CORRECT ANSWER IS ALREADY PROVIDED. I REALLY NEED FBD. The roof truss shown carries roof loads, where P = 10 kN. The truss is consisting of circular arcs top andbottom chords with radii R + h and R, respectively.Given: h = 1.2 m, R = 10 m, s = 2 m.Allowable member stresses:Tension = 250 MPaCompression = 180 MPa1. If member KL has square section, determine the minimum dimension (mm).2. If member KL has circular section, determine the minimum diameter (mm).3. If member GH has circular section, determine the minimum diameter (mm).ANSWERS: (1) 31.73 mm; (2) 35.81 mm; (3) 18.49 mmarrow_forwardPROBLEM 3.23 3.23 Under normal operating condi- tions a motor exerts a torque of magnitude TF at F. The shafts are made of a steel for which the allowable shearing stress is 82 MPa and have diameters of dCDE=24 mm and dFGH = 20 mm. Knowing that rp = 165 mm and rg114 mm, deter- mine the largest torque TF which may be exerted at F. TF F rG- rp B CH TE Earrow_forward1. (16%) (a) If a ductile material fails under pure torsion, please explain the failure mode and describe the observed plane of failure. (b) Suppose a prismatic beam is subjected to equal and opposite couples as shown in Fig. 1. Please sketch the deformation and the stress distribution of the cross section. M M Fig. 1 (c) Describe the definition of the neutral axis. (d) Describe the definition of the modular ratio.arrow_forward
- using the theorem of three moments, find all the moments, I only need concise calculations with minimal explanations. The correct answers are provided at the bottomarrow_forwardMechanics of materialsarrow_forwardusing the theorem of three moments, find all the moments, I need concise calculations onlyarrow_forward
 Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
