Calculus: Early Transcendentals, 2nd Edition

2nd Edition

ISBN: 9780321965165

Author: William L. Briggs, Lyle Cochran, Bernard Gillett

Publisher: PEARSON

See similar textbooks

Concept explainers

Arc Length

Arc length can be thought of as the distance you would travel if you walked along the path of a curve. Arc length is used in a wide range of real applications. We might be interested in knowing how far a rocket travels if it is launched along a parabolic…

Line Integral

A line integral is one of the important topics that are discussed in the calculus syllabus. When we have a function that we want to integrate, and we evaluate the function alongside a curve, we define it as a line integral. Evaluation of a function along…

Triple Integral

Examples:

Videos

Textbook Question

Chapter 14.1, Problem 40E

Equipotential curves Consider the following potential functions and graphs of their equipotential curves.

a. Find the associated gradient field F = ▿ϕ.

b. Show that the vector field is orthogonal to the equipotential curve at the point (1, 1). Illustrate this result on the figure.

c. Show that the vector field is orthogonal to the equipotential curve at all points (x, y).

d. Sketch two flow curves representing F that are everywhere orthogonal to the equipotential curves.

40. ϕ (x, y) = x²+ 2y²

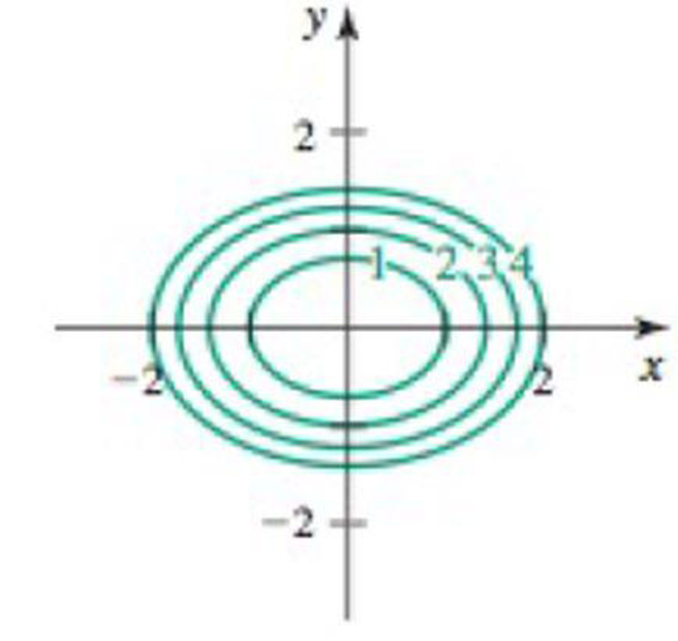
Chapter 14.1, Problem 40E, Equipotential curves Consider the following potential functions and graphs of their equipotential

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 14.1, Problem 39E

Chapter 14.1, Problem 41E

Students have asked these similar questions

Determine if each of the following vector fields is the gradient of a function f(x, y). If so, find all of the functions with this gradient. (a) (3x² + e¹0) i + (10x e¹0 - 9 siny) j (b) (10x el0y 9 sin y) i + (3x² + e¹0y) j a) I have placed my work and my answer on my answer sheet

Gradient fields on curves For the potential function φ and points A, B, C, and D on the level curve φ(x, y) = 0, complete the following steps.a. Find the gradient field F = ∇φ.b. Evaluate F at the points A, B, C, and D.c. Plot the level curve φ(x, y) = 0 and the vectors F at the points A, B, C, and D. φ(x, y) = y - 2x; A(-1, -2), B(0, 0), C(1, 2), and D(2, 4)

3. Let f(x, y) = sin x + sin y. (NOTE: You may use software for any part of this problem.) (a) Plot a contour map of f. (b) Find the gradient Vf. (c) Plot the gradient vector field Vf. (d) Explain how the contour map and the gradient vector field are related. (e) Plot the flow lines of Vf. (f) Explain how the flow lines and the vector field are related. (g) Explain how the flow lines of Vf and the contour map are related.

Chapter 14 Solutions

Calculus: Early Transcendentals, 2nd Edition

Ch. 14.1 - How is a vector field F = f, g, h used to describe...Ch. 14.1 - Sketch the vector field F = x, y.Ch. 14.1 - Prob. 3E Ch. 14.1 - Prob. 4E Ch. 14.1 - Interpret the gradient field of the temperature...Ch. 14.1 - Two-dimensional vector fields Sketch the following...Ch. 14.1 - Two-dimensional vector fields Sketch the following...Ch. 14.1 - Two-dimensional vector fields Sketch the following...Ch. 14.1 - Two-dimensional vector fields Sketch the following...Ch. 14.1 - Two-dimensional vector fields Sketch the following...

Additional Math Textbook Solutions

Find more solutions based on key concepts

Assessment 1-1A The following is a magic square all rows, columns, and diagonals sum to the same number. Find t...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

2. Reported Versus Measured In a survey of 1046 adults conducted by Bradley Corporation, subjects were asked ho...

Elementary Statistics (13th Edition)

Matching In Exercises 17–20, match the level of confidence c with the appropriate confidence interval. Assume e...

Elementary Statistics: Picturing the World (7th Edition)

Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...

A First Course in Probability (10th Edition)

Cylinder and paraboloids Find the volume of the region bounded below by the paraboloid z = x2 + y2, laterally b...

University Calculus: Early Transcendentals (4th Edition)

Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...

College Algebra (7th Edition)

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.