
GO Fresh water flows horizontally from pipe section 1 of cross-sectional area A1 into pipe section 2 of cross-sectional area A2. Figure 14-52 gives a plot of the pressure difference p2 − p1 versus the inverse area squared
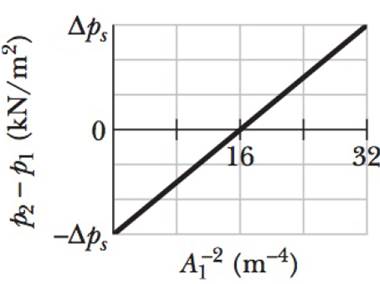
Figure 14-52 Problem 68.
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
FUNDAMENTALS OF PHYSICS (LLF)+WILEYPLUS
Additional Science Textbook Solutions
Biological Science (6th Edition)
Campbell Biology (11th Edition)
Chemistry: The Central Science (14th Edition)
Introductory Chemistry (6th Edition)
College Physics: A Strategic Approach (3rd Edition)
Cosmic Perspective Fundamentals
- When a warm front advances up and over a cold front, what is it called? front inversion stationary front cold front occlusion warm front occlusionarrow_forward1) Consider two positively charged particles, one of charge q0 (particle 0) fixed at the origin, and another of charge q1 (particle 1) fixed on the y-axis at (0,d1,0). What is the net force F→ on particle 0 due to particle 1? Express your answer (a vector) using any or all of k, q0, q1, d1, i^, j^, and k^. 2) Now add a third, negatively charged, particle, whose charge is −q2− (particle 2). Particle 2 fixed on the y-axis at position (0,d2,0). What is the new net force on particle 0, from particle 1 and particle 2? Express your answer (a vector) using any or all of k, q0, q1, q2, d1, d2, i^, j^, and k^. 3) Particle 0 experiences a repulsion from particle 1 and an attraction toward particle 2. For certain values of d1 and d2, the repulsion and attraction should balance each other, resulting in no net force. For what ratio d1/d2 is there no net force on particle 0? Express your answer in terms of any or all of the following variables: k, q0, q1, q2.arrow_forwardA 85 turn, 10.0 cm diameter coil rotates at an angular velocity of 8.00 rad/s in a 1.35 T field, starting with the normal of the plane of the coil perpendicular to the field. Assume that the positive max emf is reached first. (a) What (in V) is the peak emf? 7.17 V (b) At what time (in s) is the peak emf first reached? 0.196 S (c) At what time (in s) is the emf first at its most negative? 0.589 x s (d) What is the period (in s) of the AC voltage output? 0.785 Sarrow_forward
- A bobsled starts at the top of a track as human runners sprint from rest and then jump into the sled. Assume they reach 40 km/h from rest after covering a distance of 50 m over flat ice. a. How much work do they do on themselves and the sled which they are pushing given the fact that there are two men of combined mass 185 kg and the sled with a mass of 200 kg? (If you haven't seen bobsledding, watch youtube to understand better what's going on.) b. After this start, the team races down the track and descends vertically by 200 m. At the finish line the sled crosses with a speed of 55 m/s. How much energy was lost to drag and friction along the way down after the men were in the sled?arrow_forwardFor what type of force is it not possible to define a potential energy expression?arrow_forward10. Imagine you have a system in which you have 54 grams of ice. You can melt this ice and then vaporize it all at 0 C. The melting and vaporization are done reversibly into a balloon held at a pressure of 0.250 bar. Here are some facts about water you may wish to know. The density of liquid water at 0 C is 1 g/cm³. The density of ice at 0 C is 0.917 g/cm³. The enthalpy of vaporization of liquid water is 2.496 kJ/gram and the enthalpy of fusion of solid water is 333.55 J/gram.arrow_forward
- Consider 1 mole of supercooled water at -10°C. Calculate the entropy change of the water when the supercooled water freezes at -10°C and 1 atm. Useful data: Cp (ice) = 38 J mol-1 K-1 Cp (water) 75J mol −1 K -1 Afus H (0°C) 6026 J mol −1 Assume Cp (ice) and Cp (water) to be independent of temperature.arrow_forwardThe molar enthalpy of vaporization of benzene at its normal boiling point (80.09°C) is 30.72 kJ/mol. Assuming that AvapH and AvapS stay constant at their values at 80.09°C, calculate the value of AvapG at 75.0°C, 80.09°C, and 85.0°C. Hint: Remember that the liquid and vapor phases will be in equilibrium at the normal boiling point.arrow_forward3. The entropy of an ideal gas is S = Nkg In V. Entropy is a state function rather than a path function, and in this problem, you will show an example of the entropy change for an ideal gas being the same when you go between the same two states by two different pathways. A. Express ASV = S2 (V2) - S₁(V1), the change in entropy upon changing the volume from V₁to V2, at fixed particle number N and energy, U. B. Express ASN = S₂(N₂) - S₁ (N₁), the change in entropy upon changing the particle number from N₁ to N2, at fixed volume V and energy U. C. Write an expression for the entropy change, AS, for a two-step process (V₁, N₁) → (V2, N₁) → (V2, N₂) in which the volume changes first at fixed particle number, then the particle number changes at fixed volume. Again, assume energy is constant.arrow_forward
- Please don't use Chatgpt will upvote and give handwritten solutionarrow_forward6. We used the constant volume heat capacity, Cv, when we talked about thermodynamic cycles. It acts as a proportionality constant between energy and temperature: dU = C₁dT. You can also define a heat capacity for constant pressure processes, Cp. You can think of enthalpy playing a similar role to energy, but for constant pressure processes δαρ C = (37) - Sup Ср ат P = ат Starting from the definition of enthalpy, H = U + PV, find the relationship between Cy and Cp for an ideal gas.arrow_forwardPure membranes of dipalmitoyl lecithin phospholipids are models of biological membranes. They melt = 41°C. Reversible melting experiments indicate that at Tm AHm=37.7 kJ mol-1. Calculate: A. The entropy of melting, ASm- B. The Gibbs free energy of melting, AGm- C. Does the membrane become more or less ordered upon melting? D. There are 32 rotatable CH2 CH2 bonds in each molecule that can rotate more freely if the membrane melts. What is the increase in multiplicity on melting a mole of bonds?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





