
Concept explainers
Figure 14-46 shows two sections of an old pipe system that runs through a hill, with distances dA = dB = 30 m and D = 110 m. On each side of the hill, the pipe radius is 2.00 cm. However, the radius of the pipe inside the hill is no longer known. To determine it, hydraulic engineers first establish that water flows through the left and right sections at 2.50 m/s. Then they release a dye in the water at point A and find that it Lakes 88.8s to reach point B. What is the average radius of the pipe within the hill?
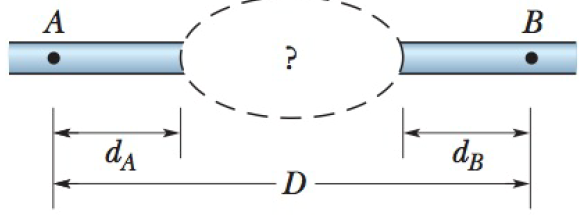
Figure 14-46 Problem 50.
Want to see the full answer?
Check out a sample textbook solution
Chapter 14 Solutions
Fundamentals of Physics Extended
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Cosmic Perspective Fundamentals
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Principles of Anatomy and Physiology
Microbiology with Diseases by Body System (5th Edition)
- PART II - RESISTORS IN SERIES Consider (but do not yet build) the circuit shown in the circuit diagram to the left, which we will call Circuit 2. Make sure you are using Bert bulbs. You may want to wire two batteries in series rather than use a single battery. 4. Predict: a) How will the brightness of bulb B₂ compare to the brighness to bulb B2B? X B2A E Y B2B Ꮓ b) How will the brightness of bulb B2A compare to the brightness of bulb B₁ from Circuit 1? c) How will the currents at points X, Y, and Z be related? d) How will the current at point X in this circuit compare to the current at point X from Circuit 1?arrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardWhat is the practical benefit (in terms of time savings and efficiency) of defining the potential energy? Be clear about what is required in terms of calculation if we do not use the concept of potential energy.arrow_forward
- What is the critical angle fir the light travelling from the crown glass(n=1.52) into the air(n=1.00)?arrow_forwardNo chatgpt pls will upvotearrow_forwardYou are working with a team that is designing a new roller coaster-type amusement park ride for a major theme park. You are present for the testing of the ride, in which an empty 150 kg car is sent along the entire ride. Near the end of the ride, the car is at near rest at the top of a 100 m tall track. It then enters a final section, rolling down an undulating hill to ground level. The total length of track for this final section from the top to the ground is 250 m. For the first 230 m, a constant friction force of 370 N acts from computer-controlled brakes. For the last 20 m, which is horizontal at ground level, the computer increases the friction force to a value required for the speed to be reduced to zero just as the car arrives at the point on the track at which the passengers exit. (a) Determine the required constant friction force (in N) for the last 20 m for the empty test car. Write AK + AU + AE int = W+Q + TMW + TMT + TET + TER for the car-track-Earth system and solve for…arrow_forward
- = 12 kg, and m3 Three objects with masses m₁ = 3.8 kg, m₂ find the speed of m3 after it moves down 4.0 m. m/s 19 kg, respectively, are attached by strings over frictionless pulleys as indicated in the figure below. The horizontal surface exerts a force of friction of 30 N on m2. If the system is released from rest, use energy concepts to m m2 m3 iarrow_forwardThree objects with masses m₁ = 3.8 kg, m₂ = 12 kg, and m 19 kg, respectively, are attached by strings over frictionless pulleys as indicated in the figure below. The horizontal surface exerts a force of friction of 30 N on m2. If the system is released from rest, use energy concepts to find the speed of m¸ after it moves down 4.0 m. m/s m m2 mgarrow_forwardIn order for Jane to return to base camp, she needs to swing across a river of width D that is filled with alligators. She must swing into a wind exerting constant horizontal force F, F = 110 N, L = 40.0 m, 0 = 50.0°, and her mass to be 50.0 kg. Wind →F Tarzan! Jane (a) with what minimum speed (in m/s) must Jane begin her swing to just make it to the other side? (If Jane can make it across with zero initial velocity, enter 0.) m/s on a vine having length L and initially making an angle with the vertical (see below figure). Take D = 48.0 m, (b) Shortly after Jane's arrival, Tarzan and Jane decide to swing back across the river (simultaneously). With what minimum speed (in m/s) must they begin their swing? Assume that Tarzan has a mass of 80.0 kg. m/sarrow_forward
- R=2.00 12V 2.00 4.00 4.002 What is the current in one of the 4.0 Q resistors? An isolated point charge q is located at point X. Two other points Y and Z are such that YZ2 XY. Y X What is (electric field at Y)/(electric field at Z)?arrow_forwardTwo objects (m₁ = 4.75 kg and m₂ 2.80 kg) are connected by a light string passing over a light, frictionless pulley as in the figure below. The 4.75-kg object is released from rest at a point h = 4.00 m above the table mg m (a) Determine the speed of each object when the two pass each other. m/s (b) Determine the speed of each object at the moment the 4.75-kg object hits the table. m/s (c) How much higher does the 2.80-kg object travel after the 4.75-kg object hits the table? marrow_forwardA cell of negligible internal resistance is connected to three identical resistors. The current in the cell is 3.0 A. The resistors are now arranged in series. What is the new current in the cell?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





