
Concept explainers
Interpretation:
The energies of rotation for ammonia,
Concept introduction:
Atoms of a molecule rotate in space about its moment of inertia. The rotational quantum number is represented by the symbol
Answer to Problem 14.98E
The energies of rotation for ammonia,
| 1 | -1 | 3753.185 |
| 1 | 0 | 1264.06 |
| 1 | 1 | 3753.185 |
| 2 | -2 | 13748.68 |
| 2 | -1 | 6281.305 |
| 2 | 0 | 3792.18 |
| 2 | 1 | 6281.305 |
| 2 | 2 | 13748.68 |
| 3 | -3 | 29986.49 |
| 3 | -2 | 17540.86 |
| 3 | -1 | 10073.49 |
| 3 | 0 | 7584.36 |
| 3 | 1 | 10073.49 |
| 3 | 2 | 17540.86 |
| 3 | 3 | 29986.49 |
| 4 | -4 | 52466.6 |
| 4 | -3 | 35042.73 |
| 4 | -2 | 22597.1 |
| 4 | -1 | 15129.73 |
| 4 | 0 | 12640.6 |
| 4 | 1 | 15129.73 |
| 4 | 2 | 22597.1 |
| 4 | 3 | 52466.6 |
| 4 | 4 | 52466.6 |
| 5 | -5 | 81189.03 |
| 5 | -4 | 58786.9 |
| 5 | -3 | 41363.03 |
| 5 | -2 | 28917.4 |
| 5 | -1 | 21450.03 |
| 5 | 0 | 18960.9 |
| 5 | 1 | 21450.03 |
| 5 | 2 | 28917.4 |
| 5 | 3 | 41363.03 |
| 5 | 4 | 58786.9 |
| 5 | 5 | 81189.03 |
| 6 | -6 | 116153.8 |
| 6 | -5 | 88773.39 |
| 6 | -4 | 66371.26 |
| 6 | -3 | 48947.39 |
| 6 | -2 | 36501.76 |
| 6 | -1 | 29034.39 |
| 6 | 0 | 26545.26 |
| 6 | 1 | 29034.39 |
| 6 | 2 | 36501.76 |
| 6 | 3 | 48947.39 |
| 6 | 4 | 66371.26 |
| 6 | 5 | 88773.39 |
| 6 | 6 | 116153.8 |
| 7 | -7 | 157360.8 |
| 7 | -6 | 125002.2 |
| 7 | -5 | 97621.81 |
| 7 | -4 | 75219.68 |
| 7 | -3 | 57795.81 |
| 7 | -2 | 45350.18 |
| 7 | -1 | 37882.81 |
| 7 | 0 | 35393.68 |
| 7 | 1 | 37882.81 |
| 7 | 2 | 45350.18 |
| 7 | 3 | 57795.81 |
| 7 | 4 | 75219.68 |
| 7 | 5 | 97621.81 |
| 7 | 6 | 125002.2 |
| 7 | 7 | 157360.8 |
| 8 | -8 | 204810.2 |
| 8 | -7 | 167473.3 |
| 8 | -6 | 135114.7 |
| 8 | -5 | 107734.3 |
| 8 | -4 | 85332.16 |
| 8 | -3 | 67908.29 |
| 8 | -2 | 55462.66 |
| 8 | -1 | 47995.29 |
| 8 | 0 | 45506.16 |
| 8 | 1 | 47995.29 |
| 8 | 2 | 55462.66 |
| 8 | 3 | 67908.29 |
| 8 | 4 | 85332.16 |
| 8 | 5 | 107734.3 |
| 8 | 6 | 135114.7 |
| 8 | 7 | 167473.3 |
| 8 | 8 | 204810.2 |
| 9 | -9 | 258501.8 |
| 9 | -8 | 216186.7 |
| 9 | -7 | 178849.8 |
| 9 | -6 | 146491.2 |
| 9 | -5 | 119110.8 |
| 9 | -4 | 96708.7 |
| 9 | -3 | 79284.83 |
| 9 | -2 | 66839.2 |
| 9 | -1 | 59371.83 |
| 9 | 0 | 56882.7 |
| 9 | 1 | 59371.83 |
| 9 | 2 | 66839.2 |
| 9 | 3 | 79284.83 |
| 9 | 4 | 96708.7 |
| 9 | 5 | 119110.8 |
| 9 | 6 | 146491.2 |
| 9 | 7 | 178849.8 |
| 9 | 8 | 216186.7 |
| 9 | 9 | 258501.8 |
| 10 | -10 | 318435.8 |
| 10 | -9 | 271142.4 |
| 10 | -8 | 228827.3 |
| 10 | -7 | 191490.4 |
| 10 | -6 | 159131.8 |
| 10 | -5 | 131751.4 |
| 10 | -4 | 109349.3 |
| 10 | -3 | 91925.43 |
| 10 | -2 | 79479.8 |
| 10 | -1 | 72012.43 |
| 10 | 0 | 69523.3 |
| 10 | 1 | 72012.43 |
| 10 | 2 | 79479.8 |
| 10 | 3 | 91925.43 |
| 10 | 4 | 109349.3 |
| 10 | 5 | 131751.4 |
| 10 | 6 | 159131.8 |
| 10 | 7 | 191490.4 |
| 10 | 8 | 228827.3 |
| 10 | 9 | 271142.4 |
| 10 | 10 | 318435.8 |
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
The energy level diagram for all the rotational levels is shown below.
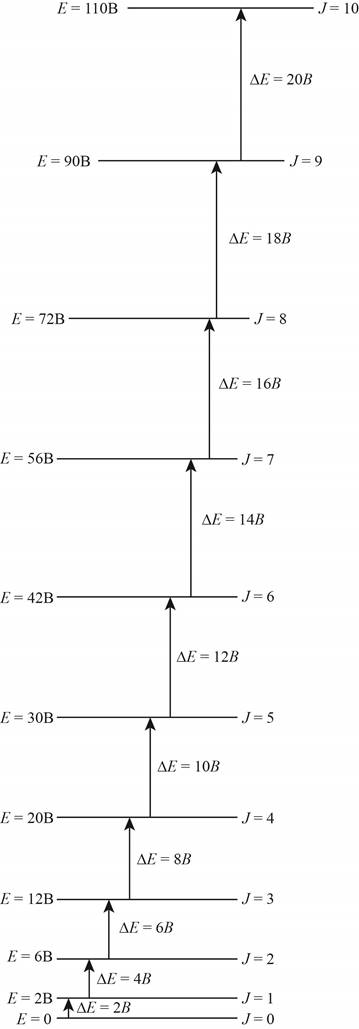
Explanation of Solution
The formula to energy of rotation (
Where,
•
•
The formula for
The formula for
Where,
•
•
The value of
Substitute the value of
The value of
Substitute the value of
The value of
The degeneracy is calculated by the formula given below.
For the rotational quantum number
The value of
The value of
Substitute the value of
Therefore, the degeneracy is
Substitute the value of
Similarly the value of
| 1 | -1 | 3753.185 |
| 1 | 0 | 1264.06 |
| 1 | 1 | 3753.185 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 2 | -2 | 13748.68 |
| 2 | -1 | 6281.305 |
| 2 | 0 | 3792.18 |
| 2 | 1 | 6281.305 |
| 2 | 2 | 13748.68 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 3 | -3 | 29986.49 |
| 3 | -2 | 17540.86 |
| 3 | -1 | 10073.49 |
| 3 | 0 | 7584.36 |
| 3 | 1 | 10073.49 |
| 3 | 2 | 17540.86 |
| 3 | 3 | 29986.49 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 4 | -4 | 52466.6 |
| 4 | -3 | 35042.73 |
| 4 | -2 | 22597.1 |
| 4 | -1 | 15129.73 |
| 4 | 0 | 12640.6 |
| 4 | 1 | 15129.73 |
| 4 | 2 | 22597.1 |
| 4 | 3 | 52466.6 |
| 4 | 4 | 52466.6 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 5 | -5 | 81189.03 |
| 5 | -4 | 58786.9 |
| 5 | -3 | 41363.03 |
| 5 | -2 | 28917.4 |
| 5 | -1 | 21450.03 |
| 5 | 0 | 18960.9 |
| 5 | 1 | 21450.03 |
| 5 | 2 | 28917.4 |
| 5 | 3 | 41363.03 |
| 5 | 4 | 58786.9 |
| 5 | 5 | 81189.03 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 6 | -6 | 116153.8 |
| 6 | -5 | 88773.39 |
| 6 | -4 | 66371.26 |
| 6 | -3 | 48947.39 |
| 6 | -2 | 36501.76 |
| 6 | -1 | 29034.39 |
| 6 | 0 | 26545.26 |
| 6 | 1 | 29034.39 |
| 6 | 2 | 36501.76 |
| 6 | 3 | 48947.39 |
| 6 | 4 | 66371.26 |
| 6 | 5 | 88773.39 |
| 6 | 6 | 116153.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 7 | -7 | 157360.8 |
| 7 | -6 | 125002.2 |
| 7 | -5 | 97621.81 |
| 7 | -4 | 75219.68 |
| 7 | -3 | 57795.81 |
| 7 | -2 | 45350.18 |
| 7 | -1 | 37882.81 |
| 7 | 0 | 35393.68 |
| 7 | 1 | 37882.81 |
| 7 | 2 | 45350.18 |
| 7 | 3 | 57795.81 |
| 7 | 4 | 75219.68 |
| 7 | 5 | 97621.81 |
| 7 | 6 | 125002.2 |
| 7 | 7 | 157360.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 8 | -8 | 204810.2 |
| 8 | -7 | 167473.3 |
| 8 | -6 | 135114.7 |
| 8 | -5 | 107734.3 |
| 8 | -4 | 85332.16 |
| 8 | -3 | 67908.29 |
| 8 | -2 | 55462.66 |
| 8 | -1 | 47995.29 |
| 8 | 0 | 45506.16 |
| 8 | 1 | 47995.29 |
| 8 | 2 | 55462.66 |
| 8 | 3 | 67908.29 |
| 8 | 4 | 85332.16 |
| 8 | 5 | 107734.3 |
| 8 | 6 | 135114.7 |
| 8 | 7 | 167473.3 |
| 8 | 8 | 204810.2 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 9 | -9 | 258501.8 |
| 9 | -8 | 216186.7 |
| 9 | -7 | 178849.8 |
| 9 | -6 | 146491.2 |
| 9 | -5 | 119110.8 |
| 9 | -4 | 96708.7 |
| 9 | -3 | 79284.83 |
| 9 | -2 | 66839.2 |
| 9 | -1 | 59371.83 |
| 9 | 0 | 56882.7 |
| 9 | 1 | 59371.83 |
| 9 | 2 | 66839.2 |
| 9 | 3 | 79284.83 |
| 9 | 4 | 96708.7 |
| 9 | 5 | 119110.8 |
| 9 | 6 | 146491.2 |
| 9 | 7 | 178849.8 |
| 9 | 8 | 216186.7 |
| 9 | 9 | 258501.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 10 | -10 | 318435.8 |
| 10 | -9 | 271142.4 |
| 10 | -8 | 228827.3 |
| 10 | -7 | 191490.4 |
| 10 | -6 | 159131.8 |
| 10 | -5 | 131751.4 |
| 10 | -4 | 109349.3 |
| 10 | -3 | 91925.43 |
| 10 | -2 | 79479.8 |
| 10 | -1 | 72012.43 |
| 10 | 0 | 69523.3 |
| 10 | 1 | 72012.43 |
| 10 | 2 | 79479.8 |
| 10 | 3 | 91925.43 |
| 10 | 4 | 109349.3 |
| 10 | 5 | 131751.4 |
| 10 | 6 | 159131.8 |
| 10 | 7 | 191490.4 |
| 10 | 8 | 228827.3 |
| 10 | 9 | 271142.4 |
| 10 | 10 | 318435.8 |
The energy level diagram for all the rotational levels is shown below.
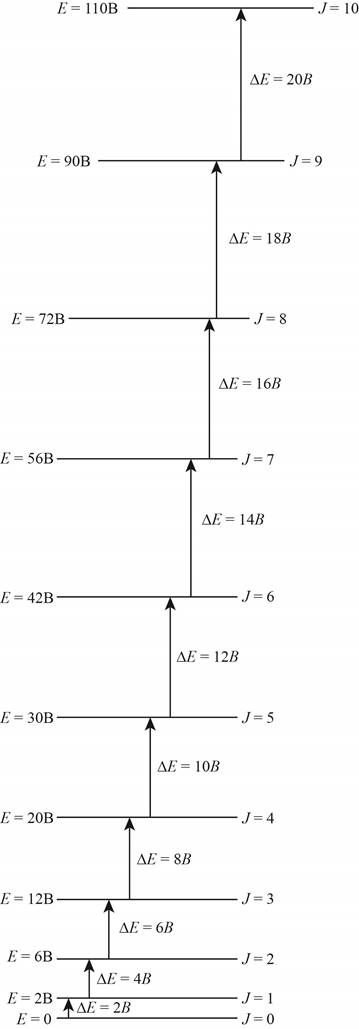
Figure 1
The energies of rotation for ammonia,
Want to see more full solutions like this?
Chapter 14 Solutions
Physical Chemistry
- What are the major products of the following enolate alkylation reaction? Please include a detailed explanation as well as a drawing as to how the reaction proceeds.arrow_forwardA block of zinc has an initial temperature of 94.2 degrees celcius and is immererd in 105 g of water at 21.90 degrees celcius. At thermal equilibrium, the final temperature is 25.20 degrees celcius. What is the mass of the zinc block? Cs(Zn) = 0.390 J/gxdegrees celcius Cs(H2O) = 4.18 J/gx degrees celcusarrow_forwardPotential Energy (kJ) 1. Consider these three reactions as the elementary steps in the mechanism for a chemical reaction. AH = -950 kJ AH = 575 kJ (i) Cl₂ (g) + Pt (s) 2C1 (g) + Pt (s) Ea = 1550 kJ (ii) Cl (g)+ CO (g) + Pt (s) → CICO (g) + Pt (s) (iii) Cl (g) + CICO (g) → Cl₂CO (g) Ea = 2240 kJ Ea = 2350 kJ AH = -825 kJ 2600 2400 2200 2000 1800 1600 1400 1200 1000 a. Draw the potential energy diagram for the reaction. Label the data points for clarity. The potential energy of the reactants is 600 kJ 800 600 400 200 0 -200- -400 -600- -800- Reaction Progressarrow_forward
- Can u help me figure out the reaction mechanisms for these, idk where to even startarrow_forwardHi, I need your help with the drawing, please. I have attached the question along with my lab instructions. Please use the reaction from the lab only, as we are not allowed to use outside sources. Thank you!arrow_forwardHi, I need your help i dont know which one to draw please. I’ve attached the question along with my lab instructions. Please use the reaction from the lab only, as we are not allowed to use outside sources. Thank you!arrow_forward
- 5. Write the formation reaction of the following complex compounds from the following reactants: 6. AgNO₃ + K₂CrO₂ + NH₄OH → 7. HgNO₃ + excess KI → 8. Al(NO₃)₃ + excess NaOH →arrow_forwardIndicate whether the product formed in the reaction exhibits tautomerism. If so, draw the structure of the tautomers. CO₂C2H5 + CH3-NH-NH,arrow_forwardDraw the major product of this reaction N-(cyclohex-1-en-1-yl)-1-(pyrrolidino) reacts with CH2=CHCHO, heat, H3O+arrow_forward
- Draw the starting material that would be needed to make this product through an intramolecular Dieckmann reactionarrow_forwardDraw the major product of this reaction. Nitropropane reacts + pent-3-en-2-one reacts with NaOCH2CH3, CH3CHOHarrow_forwardIndicate whether the product formed in the reaction exhibits tautomerism. If so, draw the structure of the tautomers. OC2H5 + CoHs-NH-NH,arrow_forward
 Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,

