
Concept explainers
A spacecraft of mass m describes a circular orbit of radius r1 around the earth. (a) Show that the additional energy ΔE that must be imparted to the spacecraft to transfer it to a circular orbit of larger radius r2 is
where M is the mass of the earth. (b) Further show that if the transfer from one circular orbit to the other is executed by placing the spacecraft on a transitional semielliptic path AB, the amounts of energy ΔEA and ΔEB which must be imparted at A and B are, respectively, proportional to r2 and r1:
Fig. P13.116
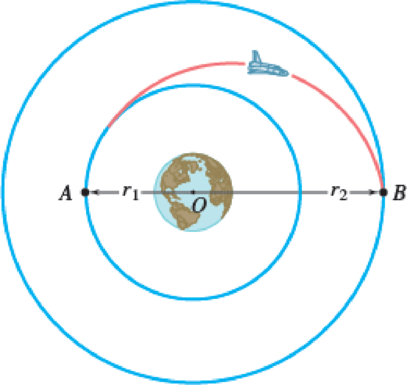
(a)
Show that additional energy
Answer to Problem 13.116P
The additional energy
Explanation of Solution
Given information:
The minimum distance between the center of the earth to the point A is
The maximum distance between the center of the earth to the point B is
The mass of the earth is M.
Calculation:
Show the figure with the force acting as in Figure (1).
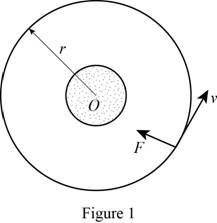
The expression for the normal acceleration
The expression for calculating the geocentric force acting on the spacecraft when it is on the surface of earth (F) as follows:
Here, G is the universal gravitational constant and M is the mass of the earth.
Calculate the velocity of the circular orbit (v) by considering the force equilibrium by taking Newton’s second law using the relation:
Substitute
The expression for the kinetic energy in the circular orbit (T) as follows;
The expression for the potential energy in the circular orbit (V) as follows;
Calculate the energy required (E) for the spacecraft using the relation:
Substitute
Substitute
The expression for the energy required for the circular orbit of radius
The expression for the energy required for the circular orbit of radius
Calculate the addition energy imparted to the spacecraft to transfer it to circular orbit
Substitute
Therefore, the additional energy
(b)
Show the transfer from one circular orbit to the other is executed by placing the spacecraft on transitional semi elliptic path AB, the amounts of energy
Answer to Problem 13.116P
The amount of energy imparted at A
Explanation of Solution
Given information:
The minimum distance between the center of the earth to the point A is
The maximum distance between the center of the earth to the point B is
The mass of the earth is M.
Calculation:
Consider the circular orbit of radius
The expression for the velocity of the circular orbit
Calculate the kinetic energy at the circular orbit
Substitute
Consider that the after the spacecraft engines are fired and it is placed on a semi-elliptic path AB.
The expression or the principle of conservation of angular momentum at point A to the point B as follows:
The expression for the kinetic energy at point B
Here, m is the mass of the satellite.
The expression for the gravitational potential energy at point B
The expression for the kinetic energy of the orbit at point A
The expression for the gravitational potential energy at point A
The expression for the principle of conservation of energy at the point A to point P as follows:
Substitute
Substitute
Simplify the Equation,
Substitute
Calculate the kinetic energy in the semi elliptic path AB
Substitute
Calculate the additional energy
Substitute
Divide and Multiply by
Substitute
Calculate the kinetic energy in the semi elliptic path AB
Substitute
Calculate the additional energy
Substitute
Divide and Multiply by
Substitute
Therefore, the amount of energy imparted at A
Want to see more full solutions like this?
Chapter 13 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- Correct answer is written below. Detailed and complete solution only with fbd. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forward
- Correct answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forward
- Correct answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you. Prefferably handwritten solution pleasearrow_forward
- Correct answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you. Prefferably handwritten solution pleasearrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you. Prefferably handwritten solution pleasearrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





