Statistics: The Art and Science of Learning from Data (4th Edition)
4th Edition
ISBN: 9780321997838
Author: Alan Agresti, Christine A. Franklin, Bernhard Klingenberg
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 74CP
Unemployment and GDP Refer to Exercise 13.67. When unemployment rate of a country is added as an additional predictor to the model already containing CO2 and percentage of population not using the Internet, we get the following output.
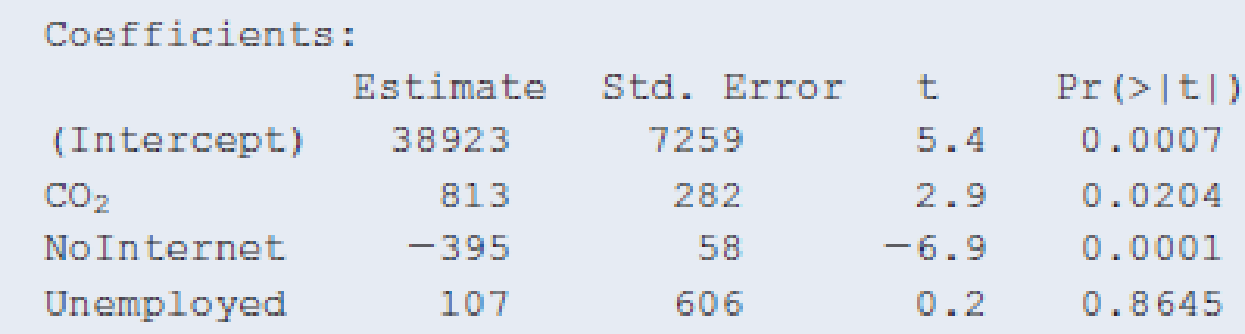
- a. Interpret the sign of the coefficient for unemployment. Is this the direction of the effect you would expect?
- b. Is the coefficient for unemployment significantly different from zero? Explain. Does this automatically mean unemployment is unrelated to GDP? (Hint: Does the effect of employment depend on other variables in the model?)
- c. What measure would you use to investigate whether unemployment helps in predicting GDP?
- d. R2 increases from 94.26% to 94.28% when adding unemployment to the model with CO2 and NoInternet. Explain what this means.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Mercury is a persistent and dispersive environmental contaminant found in many ecosystems around the world. When released as an industrial by-product, it often finds its way into aquatic systems where it can have deleterious effects on various avian and aquatic species. The accompanying data on blood mercury concentration (µg/g) for adult females near contaminated rivers in a state was read from a graph in an article.
0.20
0.23
0.24
0.30
0.35
0.41
0.54
0.57
1.43
1.70
1.82
2.20
2.24
3.08
3.24
(a)
Determine the values of the sample mean and sample median.
Hint:
xi = 18.55.
(Round your answers to four decimal places.)
x==
Explain why they are different.
The sample mean and sample median are never equal.They aren't different since the data is symmetric. There is heavy negative skewness in the data.There are an odd number of data values.There is heavy positive skewness in the data.
(b)
Determine the value of the 10% trimmed mean.…
Mercury is a persistent and dispersive environmental contaminant found in many ecosystems around the world. When released as an industrial by-product, it often finds its way into aquatic systems where it can have deleterious effects on various avian and aquatic species. The accompanying data on blood mercury concentration (µg/g) for adult females near contaminated rivers in a state was read from a graph in an article.
0.20
0.23
0.26
0.30
0.35
0.41
0.54
0.57
1.43
1.70
1.84
2.20
2.24
3.08
3.26
(a) Determine the values of the sample mean and sample median. [Hint: Σxi = 18.61.] (Round your answers to four decimal places.)
-
x = ?
~
x = ?
Explain why they are different.
There is heavy positive skewness in the data.
They aren't different since the data is symmetric.
There are an odd number of data values.
There is heavy negative skewness in the data.
The sample mean and sample median are never equal.
(b) Determine the value of the 10% trimmed mean. (Round your answer to…
solve a,b,c and d given in the image provided.
Chapter 13 Solutions
Statistics: The Art and Science of Learning from Data (4th Edition)
Ch. 13.1 - Predicting weight For a study of female college...Ch. 13.1 - Prob. 2PBCh. 13.1 - Predicting college GPA For all students at Walden...Ch. 13.1 - Prob. 4PBCh. 13.1 - Does more education cause more crime? The FL Crime...Ch. 13.1 - Crime rate and income Refer to the previous...Ch. 13.1 - The economics of golf The earnings of a PGA Tour...Ch. 13.1 - Prob. 8PBCh. 13.1 - Controlling can have no effect Suppose that the...Ch. 13.1 - House selling prices Using software with the House...
Ch. 13.1 - Used cars The following data (also available from...Ch. 13.2 - Predicting sports attendance Keeneland Racetrack...Ch. 13.2 - Predicting weight Lets use multiple regression to...Ch. 13.2 - Prob. 14PBCh. 13.2 - Price of used cars For the 19 used cars listed in...Ch. 13.2 - Prob. 16PBCh. 13.2 - Softball data For the Softball data set on the...Ch. 13.2 - Slopes, correlations, and units In Example 2 on y...Ch. 13.2 - Predicting college GPA Using software with the...Ch. 13.3 - Predicting GPA For the 59 observations in the...Ch. 13.3 - Study time help GPA? Refer to the previous...Ch. 13.3 - Variability in college GPA Refer to the previous...Ch. 13.3 - Does leg press help predict body strength? Chapter...Ch. 13.3 - Prob. 24PBCh. 13.3 - Interpret strength variability Refer to the...Ch. 13.3 - Any predictive power? Refer to the previous three...Ch. 13.3 - Predicting pizza revenue Aunt Ermas Pizza...Ch. 13.3 - Prob. 28PBCh. 13.3 - Mental health again Refer to the previous...Ch. 13.3 - Prob. 30PBCh. 13.3 - House prices Use software to do further analyses...Ch. 13.4 - Body weight residuals Examples 47 used multiple...Ch. 13.4 - Strength residuals In Chapter 12, we analyzed...Ch. 13.4 - Prob. 34PBCh. 13.4 - Nonlinear effects of age Suppose you fit a...Ch. 13.4 - Prob. 36PBCh. 13.4 - Why inspect residuals? When we use multiple...Ch. 13.4 - College athletes The College Athletes data set on...Ch. 13.4 - House prices Use software with the House Selling...Ch. 13.4 - Prob. 40PBCh. 13.5 - U.S. and foreign used cars Refer to the used car...Ch. 13.5 - Prob. 42PBCh. 13.5 - Predict using house size and condition For the...Ch. 13.5 - Quality and productivity The table shows data from...Ch. 13.5 - Predicting hamburger sales A chain restaurant that...Ch. 13.5 - Prob. 46PBCh. 13.5 - House size and garage interact? Refer to the...Ch. 13.5 - Prob. 48PBCh. 13.5 - Comparing sales You own a gift shop that has a...Ch. 13.6 - Prob. 50PBCh. 13.6 - Prob. 51PBCh. 13.6 - Prob. 52PBCh. 13.6 - Prob. 53PBCh. 13.6 - Prob. 54PBCh. 13.6 - Prob. 55PBCh. 13.6 - Prob. 56PBCh. 13.6 - Prob. 57PBCh. 13.6 - Prob. 58PBCh. 13.6 - Prob. 59PBCh. 13 - House prices This chapter has considered many...Ch. 13 - Prob. 61CPCh. 13 - Prob. 62CPCh. 13 - Prob. 63CPCh. 13 - Prob. 64CPCh. 13 - Prob. 65CPCh. 13 - Prob. 66CPCh. 13 - Prob. 67CPCh. 13 - Prob. 68CPCh. 13 - Prob. 69CPCh. 13 - AIDS and AZT In a study (reported in the New York...Ch. 13 - Factors affecting first home purchase The table...Ch. 13 - Unemployment and GDP Refer to Exercise 13.67. When...Ch. 13 - Prob. 75CPCh. 13 - Prob. 76CPCh. 13 - Prob. 77CPCh. 13 - Prob. 78CPCh. 13 - Prob. 79CPCh. 13 - True or false: Slopes For data on y = college GPA,...Ch. 13 - Prob. 81CPCh. 13 - Lurking variable Give an example of three...Ch. 13 - Prob. 83CPCh. 13 - Prob. 84CPCh. 13 - Prob. 85CPCh. 13 - Logistic versus linear For binary response...Ch. 13 - Prob. 87CPCh. 13 - Prob. 88CPCh. 13 - Prob. 89CPCh. 13 - Prob. 90CPCh. 13 - Prob. 91CPCh. 13 - Prob. 92CPCh. 13 - Prob. 93CP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Cable TV The following table shows the number C. in millions, of basic subscribers to cable TV in the indicated year These data are from the Statistical Abstract of the United States. Year 1975 1980 1985 1990 1995 2000 C 9.8 17.5 35.4 50.5 60.6 60.6 a. Use regression to find a logistic model for these data. b. By what annual percentage would you expect the number of cable subscribers to grow in the absence of limiting factors? c. The estimated number of subscribers in 2005 was 65.3million. What light does this shed on the model you found in part a?arrow_forwardDoes a linear, exponential, or logarithmic model best fit the data in Table 2? Find the model.arrow_forwardTable 6 shows the population, in thousands, of harbor seals in the Wadden Sea over the years 1997 to 2012. a. Let x represent time in years starting with x=0 for the year 1997. Let y represent the number of seals in thousands. Use logistic regression to fit a model to these data. b. Use the model to predict the seal population for the year 2020. c. To the nearest whole number, what is the limiting value of this model?arrow_forward
- Is carbon dating? Why does it work? Give an example in which carbon dating would be useful.arrow_forwardLife Expectancy The following table shows the average life expectancy, in years, of a child born in the given year42 Life expectancy 2005 77.6 2007 78.1 2009 78.5 2011 78.7 2013 78.8 a. Find the equation of the regression line, and explain the meaning of its slope. b. Plot the data points and the regression line. c. Explain in practical terms the meaning of the slope of the regression line. d. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 2019? e. Based on the trend of the regression line, what do you predict as the life expectancy of a child born in 1580?2300arrow_forwardTable 2 shows a recent graduate’s credit card balance each month after graduation. a. Use exponential regression to fit a model to these data. b. If spending continues at this rate, what will the graduate’s credit card debt be one year after graduating?arrow_forward
- What might a scatterplot of data points look like if it were best described by a logarithmic model?arrow_forwardUse the data to develop a regression equationthat could be used to predict the quantity of pork sold during future periods. Discuss how you can tell whether heteroscedasticity, autocorrelation, or multi-collinearity might be a problem.arrow_forwardC6. We present SPSS output examining the relationship between education (measured in years) and television viewing per day (measured in hours) based on a GSS 2018 subsample. As we predicted in the SPSS Demonstration, we hypothesize that as educational attainment increases, hours of television viewing will decrease, indicating a negative relationship between the two variables. Discuss the significance of the overall model based on F and its p values. Is the relationship between education and television viewing significant? Linear Regression Output for Hours Spent per Day Watching Television and Education Model Summary Adjusted R Square Std. Error of the Estimate Model R. R Square 1. .204a .042 .040 3.176 a. Predictors: (Constant), Highest year of school completed ANOVA Sum of Squares df Mean Square Sig. Model 322.181 31.945 .000 Regression 322.181 734 10.085 Residual 7402.683 7724.864 735 Total a. Dependent Variable: Hours per day watching TV b. Predictors: (Constant), Highest year of…arrow_forward
- Assume there is a positive linear correlation between the variable R (Return rate in percent of a financial investment) and the variable t (age in years of the investment) given by the regression equation R= 2.3t + 4.8 A. Without further information, can we assume there is a cause-and-effect relationship between the return rate and the age of the investment? B. If the investment continues to grow at a constant rate, what is the expeted return rate when the investment is 7 years old? C. If the investment continues to grow at a constant rate, how old is the investment when the return rate is 30%?arrow_forwardThe following data represent the population of a country An ecologist is interested in building a model that describes the population (a) Treating the year as the independent variable and the population as the dependent variable, use a graphing utility to fit a logistic model from the data. Population, y 76,212.200 92,228,500 106,021,500 123,202,600 132,164,600 151,325,800 179,323,200 203,302,000 226,542.200 248,709,900 281,421,900 Year, x Find the values for a, b and c in a logistic model of the form y = 1900 1910 -bx 1+ae 1920 1930 1940 1950 1960 1970 1980 1990 2000 (Use scientific notation. Round to five decimal places as needed) b- (Round to four decimal places as needed) (Round to one decimal place as needed.) (b) Graph the data together with the logistic function found in part (a) on a scatter diagram Which graph correctly illustrates the logistic growth model for this data? OA. 0.000.000 Q 2010 76000 000 O B. 20. 2010 16.000.000 OC. 2010 71.000 000 () Time Remaining: 00404 ofarrow_forwardABC Corporation has sales figures as given below. Forecast sales for 2021 using the following techniques: (a) the trend line method. Mention the equation and the R square value obtained. (b) Three year moving average method. (c) Exponential Smoothening Method with a smoothening constant of 0.8.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Correlation Vs Regression: Difference Between them with definition & Comparison Chart; Author: Key Differences;https://www.youtube.com/watch?v=Ou2QGSJVd0U;License: Standard YouTube License, CC-BY
Correlation and Regression: Concepts with Illustrative examples; Author: LEARN & APPLY : Lean and Six Sigma;https://www.youtube.com/watch?v=xTpHD5WLuoA;License: Standard YouTube License, CC-BY