Linear Algebra with Applications (2-Download)
5th Edition
ISBN: 9780321796974
Author: Otto Bretscher
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 1.3, Problem 49E
Consider the accompanying table. For some linear systems
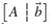In each case, state whether the system couldhave no solution, one solution, or infinitely many solutions. There may be more than one possibility for somesystems. Justify your answers.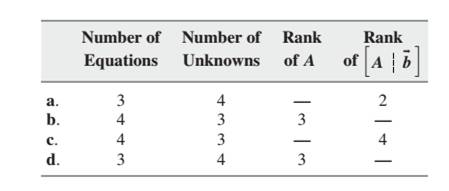
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Use the graph to solve 3x2-3x-8=0
Într-un bloc sunt apartamente cu 2 camere și apartamente cu 3 camere , în total 20 de apartamente și 45 de camere.Calculați câte apartamente sunt cu 2 camere și câte apartamente sunt cu 3 camere.
1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set
Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k
components, where k is the greatest common divisor of {n, r,s}.
Chapter 1 Solutions
Linear Algebra with Applications (2-Download)
Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...
Ch. 1.1 - In Exercises 11 through 13,find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 14 through 16,find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - Find all solutions of the linear system | x+2y=a...Ch. 1.1 - Find all solutions of the linear system...Ch. 1.1 - Consider the linear system...Ch. 1.1 - Consider the linear system |x+yz=2x+2y+z=3x+y+( k...Ch. 1.1 - The sums of any two of three real numbers are 24,...Ch. 1.1 - Emile and Gertrude are brother and sister. Emile...Ch. 1.1 - Consider a two-commodity market. When the...Ch. 1.1 - The Russian-born U.S. economist and Nobel laureate...Ch. 1.1 - Find the outputs a andb needed to satisfy the...Ch. 1.1 - Consider the differential equation...Ch. 1.1 - Find all solutions of the system |7xy=x6x+8y=y| ,...Ch. 1.1 - On a sunny summer day, you are taking the...Ch. 1.1 - On your next trip to Switzerland, you should take...Ch. 1.1 - In a grid of wires, the temperature at exterior...Ch. 1.1 - Find the polynomial of degree 2 [a polynomial of...Ch. 1.1 - Find a polynomial of degree 2 [of the form...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find the function f(t) of the form f(t)=ae3t+be2t...Ch. 1.1 - Find the function f(t) of the form...Ch. 1.1 - Prob. 39ECh. 1.1 - Find the ellipse centered at the origin that runs...Ch. 1.1 - Find all points (a,b,c) in space for which the...Ch. 1.1 - Linear systems are particularly easy to solve when...Ch. 1.1 - Consider the linear system |x+y=1x+ t 2y=t| ,...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Boris and Marina are shopping for chocolate bars....Ch. 1.1 - Here is another method to solve a system of linear...Ch. 1.1 - A hermit eats only two kinds of food: brown rice...Ch. 1.1 - I have 32 bills in my wallet, in the denominations...Ch. 1.1 - Some parking meters in Milan, Italy, accept coins...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Prob. 16ECh. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Determine which of the matrices below are in...Ch. 1.2 - Find all 41 matrices in reduced row-echelon form.Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - We say that two nm matrices in reduced...Ch. 1.2 - How many types of 32 matrices in reduced...Ch. 1.2 - How many types of 23 matrices in reduced...Ch. 1.2 - Prob. 25ECh. 1.2 - Suppose matrix A is transformed into matrix B...Ch. 1.2 - Prob. 27ECh. 1.2 - Consider an nm in matrix A. Can you transform...Ch. 1.2 - Prob. 29ECh. 1.2 - Suppose you subtract a multiple of an equation in...Ch. 1.2 - Balancing a chemical reaction. Consider the...Ch. 1.2 - Find the polynomial of degree 3 [a polynomial of...Ch. 1.2 - Find the polynomial of degree 4 whose graph...Ch. 1.2 - Cubic splines. Suppose you are in charge of the...Ch. 1.2 - Find the polynomial f(t) of degree 3 such that...Ch. 1.2 - The dot product of two vectors x=[ x 1 x 2 x n]...Ch. 1.2 - Find all vectors in 4 that are perpendicular to...Ch. 1.2 - Find all solutions x1,x2,x3 of the equation...Ch. 1.2 - Prob. 39ECh. 1.2 - If we consider more than three industries in an...Ch. 1.2 - Consider the economy of Israel in 1958.11 The...Ch. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - The accompanying sketch represents a maze of...Ch. 1.2 - Let S(t) be the length of the tth day of the year...Ch. 1.2 - Prob. 46ECh. 1.2 - Consider the equations...Ch. 1.2 - Consider the equations |y+2kz=0x+2y+6z=2kx+2z=1| ,...Ch. 1.2 - a. Find all solutions x1,x2,x3,x4 of the system...Ch. 1.2 - For an arbitrary positive integer n3 , find all...Ch. 1.2 - Prob. 51ECh. 1.2 - Find all the polynomials f(t) of degree 3 such...Ch. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Students are buying books for the new semester....Ch. 1.2 - Prob. 64ECh. 1.2 - At the beginning of a political science class at a...Ch. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Pigeons are sold at the rate of 5 for 3 panas,...Ch. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.3 - GOAL Use the reduced row-echelon form of the...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - a. Write the system |x+2y=73x+y=11| in vector...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 (sketched in...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 shown in the...Ch. 1.3 - Consider the vectors v1,v2,v3,v4 in 2 shown in...Ch. 1.3 - Write the system |x+2y+3z=14x+5y+6z=47x+8y+9z=9|...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - a. Find [234567]+[753101] . b. Find 9[112345] .Ch. 1.3 - Use technology to compute the product...Ch. 1.3 - Consider a linear system of three equations with...Ch. 1.3 - Consider a linear system of four equations with...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 43 matrix, and let b and c be two...Ch. 1.3 - If the rank of a 44 matrix A is 4, what is...Ch. 1.3 - If the rank of a 53 matrix A is 3, what is...Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - Let A be the nn matrix with all 1‘s on the...Ch. 1.3 - We define the vectors e1=[001],e2=[010],e3=[001]...Ch. 1.3 - In m , we define ei=[0010]ithcomponent . If A is...Ch. 1.3 - Find a 33 matrix A such that...Ch. 1.3 - Find all vectors x such that Ax=b , where...Ch. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Consider an nm matrix A with more rows than...Ch. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - A linear system of the form Ax=0 is called...Ch. 1.3 - Consider a solution x1 of the linear system Ax=b...Ch. 1.3 - Consider the accompanying table. For some linear...Ch. 1.3 - Consider a linear system Ax=b , where A is a 43...Ch. 1.3 - Consider an nm matrix A, an rs matrix B, and...Ch. 1.3 - Consider the matrices A=[1012] and B=[0110] .Can...Ch. 1.3 - If A and B are two nm matrices, is (A+B)x=Ax+Bx...Ch. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Is the vector [301385662] a linear combination of...Ch. 1.3 - Prob. 57ECh. 1.3 - For which values of the constants b and c is the...Ch. 1.3 - For which values of the constants c and d is...Ch. 1.3 - For which values of the constants a, b, c and d is...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Let A be the nn matrix with 0’s on the main...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - Matrix [120001000] is in reduced row-echelon form.Ch. 1 - A system of four linear equations in three...Ch. 1 - There exists a 34 matrix with rank 4.Ch. 1 - If A is a 34 matrix and vector v is in 4 , then...Ch. 1 - If the 44 matrix A has rank 4, then any linear...Ch. 1 - There exists a system of three linear equations...Ch. 1 - There exists a 55 matrix A of rank 4 such that the...Ch. 1 - If matrix A is in reduced row-echelon form, then...Ch. 1 - The system [123456000]x=[123] is inconsistent.Ch. 1 - There exists 22 matrix A such that A=[12]=[34] .Ch. 1 - If A is a nonzero matrix of the form [abba] , then...Ch. 1 - rank [111123136]=3Ch. 1 - The system Ax=[0001] is inconsistent for all 43...Ch. 1 - There exists a 22 matrix A such that A=[11]=[12]...Ch. 1 - rank [222222222]=2Ch. 1 - [111315171921][131]=[131921]Ch. 1 - There exists a matrix A such that A=[12]=[357] .Ch. 1 - Vector [123] is a linear combination of vectors...Ch. 1 - If the system Ax=b has a unique solution, then...Ch. 1 - If A is any 43 matrix, then there exists a vector...Ch. 1 - There exist scalars a and b such that matrix...Ch. 1 - If v and w are vectors in 4 , then v must be a...Ch. 1 - If u,v , and w are nonzero vectors in 2 , then w...Ch. 1 - If v and w are vectors in 4 , then the zero vector...Ch. 1 - If A and B are any two 33 matrices of rank2,then...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - A linear system with fewer unknowns than...Ch. 1 - The rank of any upper triangular matrix is the...Ch. 1 - There exists a 43 matrix A of rank 3 such that...Ch. 1 - The system Ax=b is inconsistent if (and only...Ch. 1 - If A is a 43 matrix of rank 3 and Au=Aw for two...Ch. 1 - If A is a 44 matrix and the system Ax=[2345] has...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - If A=[uvw] and rref(A)=[002013000] , then the...Ch. 1 - If A and B are matrices of the same size, then the...Ch. 1 - If A and B are any two nn matrices of rank n, then...Ch. 1 - If a vector v in 4 is a linear combination of u...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - The linear system Ax=b consistent if (and only if)...Ch. 1 - If A is a 34 matrix of rank 3, then the system...Ch. 1 - If two matrices A and B have the same reduced...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - If A and B are two 22 matrices such that the...Ch. 1 - A lower triangular 33 matrix has rank 3 if (and...Ch. 1 - If adbc0 , then the matrix [abcd] must have rank...Ch. 1 - If vector w is a linear combination of u and v ,...Ch. 1 - If the linear system Ax=b has a unique solution...Ch. 1 - A matrix is called a 0-1-matrix if all of its...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Question 3 over a field K. In this question, MË(K) denotes the set of n × n matrices (a) Suppose that A Є Mn(K) is an invertible matrix. Is it always true that A is equivalent to A-¹? Justify your answer. (b) Let B be given by 8 B = 0 7 7 0 -7 7 Working over the field F2 with 2 elements, compute the rank of B as an element of M2(F2). (c) Let 1 C -1 1 [4] [6] and consider C as an element of M3(Q). Determine the minimal polynomial mc(x) and hence, or otherwise, show that C can not be diagonalised. [7] (d) Show that C in (c) considered as an element of M3(R) can be diagonalised. Write down all the eigenvalues. Show your working. [8]arrow_forwardR denotes the field of real numbers, Q denotes the field of rationals, and Fp denotes the field of p elements given by integers modulo p. You may refer to general results from lectures. Question 1 For each non-negative integer m, let R[x]m denote the vector space consisting of the polynomials in x with coefficients in R and of degree ≤ m. x²+2, V3 = 5. Prove that (V1, V2, V3) is a linearly independent (a) Let vi = x, V2 = list in R[x] 3. (b) Let V1, V2, V3 be as defined in (a). Find a vector v € R[×]3 such that (V1, V2, V3, V4) is a basis of R[x] 3. [8] [6] (c) Prove that the map ƒ from R[x] 2 to R[x]3 given by f(p(x)) = xp(x) — xp(0) is a linear map. [6] (d) Write down the matrix for the map ƒ defined in (c) with respect to the basis (2,2x + 1, x²) of R[x] 2 and the basis (1, x, x², x³) of R[x] 3. [5]arrow_forwardQuestion 4 (a) The following matrices represent linear maps on R² with respect to an orthonormal basis: = [1/√5 2/√5 [2/√5 -1/√5] " [1/√5 2/√5] A = B = [2/√5 1/√5] 1 C = D = = = [ 1/3/5 2/35] 1/√5 2/√5 -2/√5 1/√5' For each of the matrices A, B, C, D, state whether it represents a self-adjoint linear map, an orthogonal linear map, both, or neither. (b) For the quadratic form q(x, y, z) = y² + 2xy +2yz over R, write down a linear change of variables to u, v, w such that q in these terms is in canonical form for Sylvester's Law of Inertia. [6] [4]arrow_forward
- part b pleasearrow_forwardQuestion 5 (a) Let a, b, c, d, e, ƒ Є K where K is a field. Suppose that the determinant of the matrix a cl |df equals 3 and the determinant of determinant of the matrix a+3b cl d+3e f ГЪ e [ c ] equals 2. Compute the [5] (b) Calculate the adjugate Adj (A) of the 2 × 2 matrix [1 2 A = over R. (c) Working over the field F3 with 3 elements, use row and column operations to put the matrix [6] 0123] A = 3210 into canonical form for equivalence and write down the canonical form. What is the rank of A as a matrix over F3? 4arrow_forwardQuestion 2 In this question, V = Q4 and - U = {(x, y, z, w) EV | x+y2w+ z = 0}, W = {(x, y, z, w) € V | x − 2y + w − z = 0}, Z = {(x, y, z, w) € V | xyzw = 0}. (a) Determine which of U, W, Z are subspaces of V. Justify your answers. (b) Show that UW is a subspace of V and determine its dimension. (c) Is VU+W? Is V = UW? Justify your answers. [10] [7] '00'arrow_forward
- Tools Sign in Different masses and Indicated velocities Rotational inert > C C Chegg 39. The balls shown have different masses and speeds. Rank the following from greatest to least: 2.0 m/s 8.5 m/s 9.0 m/s 12.0 m/s 1.0 kg A 1.2 kg B 0.8 kg C 5.0 kg D C a. The momenta b. The impulses needed to stop the balls Solved 39. The balls shown have different masses and speeds. | Chegg.com Images may be subject to copyright. Learn More Share H Save Visit > quizlet.com%2FBoyE3qwOAUqXvw95Fgh5Rw.jpg&imgrefurl=https%3A%2F%2Fquizlet.com%2F529359992%2Fc. Xarrow_forwardSimplify the below expression. 3 - (-7)arrow_forward(6) ≤ a) Determine the following groups: Homz(Q, Z), Homz(Q, Q), Homz(Q/Z, Z) for n E N. Homz(Z/nZ, Q) b) Show for ME MR: HomR (R, M) = M.arrow_forward
- 1. If f(x² + 1) = x + 5x² + 3, what is f(x² - 1)?arrow_forward2. What is the total length of the shortest path that goes from (0,4) to a point on the x-axis, then to a point on the line y = 6, then to (18.4)?arrow_forwardموضوع الدرس Prove that Determine the following groups Homz(QZ) Hom = (Q13,Z) Homz(Q), Hom/z/nZ, Qt for neN- (2) Every factor group of adivisible group is divisble. • If R is a Skew ficald (aring with identity and each non Zero element is invertible then every R-module is free.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Vector Spaces | Definition & Examples; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=72GtkP6nP_A;License: Standard YouTube License, CC-BY
Understanding Vector Spaces; Author: Professor Dave Explains;https://www.youtube.com/watch?v=EP2ghkO0lSk;License: Standard YouTube License, CC-BY