
Linear Algebra with Applications (2-Download)
5th Edition
ISBN: 9780321796974
Author: Otto Bretscher
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1.1, Problem 25E
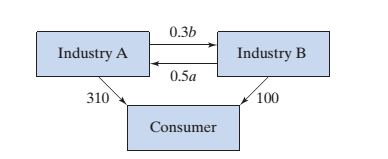
Find the outputs a andb needed to satisfy the consumerand interindustry demands given in the following figure.See Exercise 24:
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem #5
Section A of my math class has 110 students. Section B of my math class has 80 students.
a). If I randomly select 15 students from the combined classes, in a way that the order of my
selection does not matter, what is the probability that all 15 students can from Section A?
b). If I randomly select 15 students from the combined classes, in a way that the order of my
selection does not matter, what is the probability that all 15 students can from Section B?
c). If I randomly select 15 students from the combined classes, in a way that the order of my
selection does not matter, what is the probability that all 7 students come from section A and 8
students come from section B?
Problem #6
A special passcode to unlock your phone consists of 4 digits where repeated digits are not
allowed. If someone were to randomly guess a 4 digit passcode, what is the probability that
they guess your passcode on the first try?
Problem #3
If a card is picked at random from a standard 52-card deck, what is the probability of getting a
black card or a queen?
Chapter 1 Solutions
Linear Algebra with Applications (2-Download)
Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...Ch. 1.1 - GOAL Set up and solve systems with as many as...
Ch. 1.1 - In Exercises 11 through 13,find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 11 through 13, find all solutions of...Ch. 1.1 - In Exercises 14 through 16,find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - In Exercises 14 through 16, find all solutions of...Ch. 1.1 - Find all solutions of the linear system | x+2y=a...Ch. 1.1 - Find all solutions of the linear system...Ch. 1.1 - Consider the linear system...Ch. 1.1 - Consider the linear system |x+yz=2x+2y+z=3x+y+( k...Ch. 1.1 - The sums of any two of three real numbers are 24,...Ch. 1.1 - Emile and Gertrude are brother and sister. Emile...Ch. 1.1 - Consider a two-commodity market. When the...Ch. 1.1 - The Russian-born U.S. economist and Nobel laureate...Ch. 1.1 - Find the outputs a andb needed to satisfy the...Ch. 1.1 - Consider the differential equation...Ch. 1.1 - Find all solutions of the system |7xy=x6x+8y=y| ,...Ch. 1.1 - On a sunny summer day, you are taking the...Ch. 1.1 - On your next trip to Switzerland, you should take...Ch. 1.1 - In a grid of wires, the temperature at exterior...Ch. 1.1 - Find the polynomial of degree 2 [a polynomial of...Ch. 1.1 - Find a polynomial of degree 2 [of the form...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find all the polynomials f(t) of degree 2 [of the...Ch. 1.1 - Find the function f(t) of the form f(t)=ae3t+be2t...Ch. 1.1 - Find the function f(t) of the form...Ch. 1.1 - Prob. 39ECh. 1.1 - Find the ellipse centered at the origin that runs...Ch. 1.1 - Find all points (a,b,c) in space for which the...Ch. 1.1 - Linear systems are particularly easy to solve when...Ch. 1.1 - Consider the linear system |x+y=1x+ t 2y=t| ,...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Find a system of linear equations with three...Ch. 1.1 - Boris and Marina are shopping for chocolate bars....Ch. 1.1 - Here is another method to solve a system of linear...Ch. 1.1 - A hermit eats only two kinds of food: brown rice...Ch. 1.1 - I have 32 bills in my wallet, in the denominations...Ch. 1.1 - Some parking meters in Milan, Italy, accept coins...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - GOAL Use Gauss-Jordan elimination to solve linear...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Prob. 16ECh. 1.2 - Solve the linear systems in Exercises 13 through...Ch. 1.2 - Determine which of the matrices below are in...Ch. 1.2 - Find all 41 matrices in reduced row-echelon form.Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - For which values of a, b, c, d, and e is the...Ch. 1.2 - We say that two nm matrices in reduced...Ch. 1.2 - How many types of 32 matrices in reduced...Ch. 1.2 - How many types of 23 matrices in reduced...Ch. 1.2 - Prob. 25ECh. 1.2 - Suppose matrix A is transformed into matrix B...Ch. 1.2 - Prob. 27ECh. 1.2 - Consider an nm in matrix A. Can you transform...Ch. 1.2 - Prob. 29ECh. 1.2 - Suppose you subtract a multiple of an equation in...Ch. 1.2 - Balancing a chemical reaction. Consider the...Ch. 1.2 - Find the polynomial of degree 3 [a polynomial of...Ch. 1.2 - Find the polynomial of degree 4 whose graph...Ch. 1.2 - Cubic splines. Suppose you are in charge of the...Ch. 1.2 - Find the polynomial f(t) of degree 3 such that...Ch. 1.2 - The dot product of two vectors x=[ x 1 x 2 x n]...Ch. 1.2 - Find all vectors in 4 that are perpendicular to...Ch. 1.2 - Find all solutions x1,x2,x3 of the equation...Ch. 1.2 - Prob. 39ECh. 1.2 - If we consider more than three industries in an...Ch. 1.2 - Consider the economy of Israel in 1958.11 The...Ch. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - The accompanying sketch represents a maze of...Ch. 1.2 - Let S(t) be the length of the tth day of the year...Ch. 1.2 - Prob. 46ECh. 1.2 - Consider the equations...Ch. 1.2 - Consider the equations |y+2kz=0x+2y+6z=2kx+2z=1| ,...Ch. 1.2 - a. Find all solutions x1,x2,x3,x4 of the system...Ch. 1.2 - For an arbitrary positive integer n3 , find all...Ch. 1.2 - Prob. 51ECh. 1.2 - Find all the polynomials f(t) of degree 3 such...Ch. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Students are buying books for the new semester....Ch. 1.2 - Prob. 64ECh. 1.2 - At the beginning of a political science class at a...Ch. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Pigeons are sold at the rate of 5 for 3 panas,...Ch. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.3 - GOAL Use the reduced row-echelon form of the...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - Find the rank of the matrices in Exercises 2...Ch. 1.3 - a. Write the system |x+2y=73x+y=11| in vector...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 (sketched in...Ch. 1.3 - Consider the vectors v1,v2,v3 in 2 shown in the...Ch. 1.3 - Consider the vectors v1,v2,v3,v4 in 2 shown in...Ch. 1.3 - Write the system |x+2y+3z=14x+5y+6z=47x+8y+9z=9|...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the dot products in Exercises 10 through...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 13 through 15...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - Compute the products Axin Exercises 16 through 19...Ch. 1.3 - a. Find [234567]+[753101] . b. Find 9[112345] .Ch. 1.3 - Use technology to compute the product...Ch. 1.3 - Consider a linear system of three equations with...Ch. 1.3 - Consider a linear system of four equations with...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 44 matrix, and let b and c be two...Ch. 1.3 - Let A be a 43 matrix, and let b and c be two...Ch. 1.3 - If the rank of a 44 matrix A is 4, what is...Ch. 1.3 - If the rank of a 53 matrix A is 3, what is...Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - In Problems 29 through 32, let x=[539]andy=[201]....Ch. 1.3 - Let A be the nn matrix with all 1‘s on the...Ch. 1.3 - We define the vectors e1=[001],e2=[010],e3=[001]...Ch. 1.3 - In m , we define ei=[0010]ithcomponent . If A is...Ch. 1.3 - Find a 33 matrix A such that...Ch. 1.3 - Find all vectors x such that Ax=b , where...Ch. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Consider an nm matrix A with more rows than...Ch. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - A linear system of the form Ax=0 is called...Ch. 1.3 - Consider a solution x1 of the linear system Ax=b...Ch. 1.3 - Consider the accompanying table. For some linear...Ch. 1.3 - Consider a linear system Ax=b , where A is a 43...Ch. 1.3 - Consider an nm matrix A, an rs matrix B, and...Ch. 1.3 - Consider the matrices A=[1012] and B=[0110] .Can...Ch. 1.3 - If A and B are two nm matrices, is (A+B)x=Ax+Bx...Ch. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Is the vector [301385662] a linear combination of...Ch. 1.3 - Prob. 57ECh. 1.3 - For which values of the constants b and c is the...Ch. 1.3 - For which values of the constants c and d is...Ch. 1.3 - For which values of the constants a, b, c and d is...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - For which values of the constant c is [1cc2] a...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - In Exercises 63 through 68, consider the vectors...Ch. 1.3 - Prob. 65ECh. 1.3 - Prob. 66ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.3 - Let A be the nn matrix with 0’s on the main...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - TRUE OR FALSE? 19 Determine whether the statements...Ch. 1 - Matrix [120001000] is in reduced row-echelon form.Ch. 1 - A system of four linear equations in three...Ch. 1 - There exists a 34 matrix with rank 4.Ch. 1 - If A is a 34 matrix and vector v is in 4 , then...Ch. 1 - If the 44 matrix A has rank 4, then any linear...Ch. 1 - There exists a system of three linear equations...Ch. 1 - There exists a 55 matrix A of rank 4 such that the...Ch. 1 - If matrix A is in reduced row-echelon form, then...Ch. 1 - The system [123456000]x=[123] is inconsistent.Ch. 1 - There exists 22 matrix A such that A=[12]=[34] .Ch. 1 - If A is a nonzero matrix of the form [abba] , then...Ch. 1 - rank [111123136]=3Ch. 1 - The system Ax=[0001] is inconsistent for all 43...Ch. 1 - There exists a 22 matrix A such that A=[11]=[12]...Ch. 1 - rank [222222222]=2Ch. 1 - [111315171921][131]=[131921]Ch. 1 - There exists a matrix A such that A=[12]=[357] .Ch. 1 - Vector [123] is a linear combination of vectors...Ch. 1 - If the system Ax=b has a unique solution, then...Ch. 1 - If A is any 43 matrix, then there exists a vector...Ch. 1 - There exist scalars a and b such that matrix...Ch. 1 - If v and w are vectors in 4 , then v must be a...Ch. 1 - If u,v , and w are nonzero vectors in 2 , then w...Ch. 1 - If v and w are vectors in 4 , then the zero vector...Ch. 1 - If A and B are any two 33 matrices of rank2,then...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - A linear system with fewer unknowns than...Ch. 1 - The rank of any upper triangular matrix is the...Ch. 1 - There exists a 43 matrix A of rank 3 such that...Ch. 1 - The system Ax=b is inconsistent if (and only...Ch. 1 - If A is a 43 matrix of rank 3 and Au=Aw for two...Ch. 1 - If A is a 44 matrix and the system Ax=[2345] has...Ch. 1 - If vector u is a linear combination of vectors v...Ch. 1 - If A=[uvw] and rref(A)=[002013000] , then the...Ch. 1 - If A and B are matrices of the same size, then the...Ch. 1 - If A and B are any two nn matrices of rank n, then...Ch. 1 - If a vector v in 4 is a linear combination of u...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - The linear system Ax=b consistent if (and only if)...Ch. 1 - If A is a 34 matrix of rank 3, then the system...Ch. 1 - If two matrices A and B have the same reduced...Ch. 1 - If matrix E is in reduced row-echelon form, and if...Ch. 1 - If A and B are two 22 matrices such that the...Ch. 1 - A lower triangular 33 matrix has rank 3 if (and...Ch. 1 - If adbc0 , then the matrix [abcd] must have rank...Ch. 1 - If vector w is a linear combination of u and v ,...Ch. 1 - If the linear system Ax=b has a unique solution...Ch. 1 - A matrix is called a 0-1-matrix if all of its...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Problem #1 In the 2010 census, it was reported that the United States had a population of 310 million people. Of those, 74 million were under the age of 18. If you chose a person from the U.S. population at random, what is the probability they are under the age of 18? Problem #2 Given a set S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, if you were choosing a number at random what is the probability that you would choose an even number or a number larger than 7?arrow_forwardComplete the table below. For solutions, round to the nearest whole number.arrow_forwardLet the universal set be whole numbers 1 through 20 inclusive. That is, U = {1, 2, 3, 4, . . ., 19, 20}. Let A, B, and C be subsets of U. Let A be the set of all prime numbers: A = {2, 3, 5, 7, 11, 13, 17, 19} Let B be the set of all odd numbers: B = {1,3,5,7, . . ., 17, 19} Let C be the set of all square numbers: C = {1,4,9,16}arrow_forward
- A research team consists of 4 senior researchers and 10 research assistants. The team needs to select 2 senior researchers and 2 research assistants to attend a conference. How many different ways can the group being sent to the conference be formed?arrow_forwardThere are 25 different varieties of flowering plants found in a natural habitat you are studying. You are asked to randomly select 5 of these flowering plant varieties to bring back to your laboratory for further study. How many different combinations of are possible? That is, how many possible 5 plant subgroups can be formed out of the 25 total plants found?arrow_forwardA person is tossing a fair, two-sided coin three times and recording the results (either a Heads, H, or a Tails, T). Let E be the event that exactly two heads are tossed. Which of the following sets represent the event E? Group of answer choices {HHT, HTH, THH} {HHT, THH} {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT} {HH}arrow_forward
- Take Quiz 54m Exit Let the universal set be whole numbers 1 through 20 inclusive. That is, U = {1, 2, 3, 4, . . ., 19, 20}. Let A, B, and C be subsets of U. Let A be the set of all prime numbers: A = {2, 3, 5, 7, 11, 13, 17, 19} Let B be the set of all odd numbers: B = {1,3,5,7, • • , 17, 19} Let C be the set of all square numbers: C = {1,4,9,16} ☐ Question 2 3 pts Which of the following statement(s) is true? Select all that apply. (1) АСВ (2) A and C are disjoint (mutually exclusive) sets. (3) |B| = n(B) = 10 (4) All of the elements in AC are even numbers. ☐ Statement 1 is true. Statement 2 is true. Statement 3 is true. Statement 4 is true.arrow_forward☐ Question 1 2 pts Let G be the set that represents all whole numbers between 5 and 12 exclusive. Which of the following is set G in standard set notation. (Roster Method)? O G = [5, 12] G = {5, 6, 7, 8, 9, 10, 11, 12} O G = (5, 12) OG = {6, 7, 8, 9, 10, 11}arrow_forwardSolve thisarrow_forward
- int/PlayerHomework.aspx?homeworkId=689099898&questionId=1&flushed=false&cid=8120746¢erw BP Physical Geograph... HW Score: 0%, 0 of 13 points ○ Points: 0 of 1 Determine if the values of the variables listed are solutions of the system of equations. 2x - y = 4 3x+5y= - 6 x=1, y = 2; (1,-2) Is (1, 2) a solution of the system of equations? L No Yes iew an example Get more help - Aarrow_forward12:01 PM Tue May 13 < AA ✓ Educatic S s3.amazona... A Assess Your... 目 accelerate-iu15-bssd.vschool.com S s3.amazona... Trigonometric Identities Module Exam Dashboard ... Dashboard ... Algebra 2 Pa... Algebra 2 Part 4 [Honors] (Acc. Ed.) (Zimmerman) 24-25 / Module 11: Trigonometric Identities i + 38% ✰ Start Page Alexis Forsythe All changes saved 10. A sound wave's amplitude can be modeled by the function y = −7 sin ((x-1) + 4). Within the interval 0 < x < 12, when does the function have an amplitude of 4? (Select all that apply.) 9.522 seconds 4.199 seconds 0.522 seconds 1.199 seconds Previous 10 of 20 Nextarrow_forwardJamal wants to save $48,000 for a down payment on a home. How much will he need to invest in an account with 11.8% APR, compounding daily, in order to reach his goal in 10 years? Round to the nearest dollar.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,


Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY