
Concept explainers
a.
Find the
Check whether a negative value of correlation coefficient is surprising or not.
Interpret the results.
a.
Answer to Problem 43CE
The
Explanation of Solution
Step-by-step procedure to obtain the correlation coefficient using MegaStat software:
- In an EXCEL sheet enter the data values of x and y.
- Go to Add-Ins > MegaStat >
Correlation/Regression > Correlation matrix. - Enter Input
Range as $A$1:$B$33. - Click on OK.
Output obtained using MegaStat is given as follows:
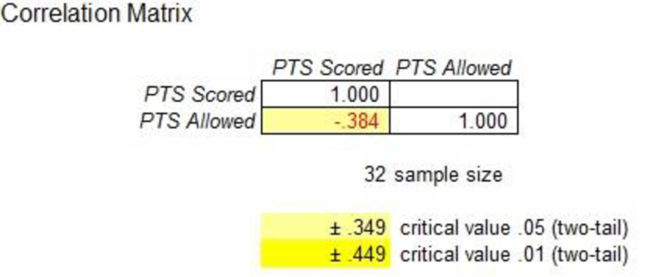
The correlation coefficient is –0.384. Since the correlation coefficient is negative, there is a moderate
b.
Find the value of coefficient of determination and explain the relationship.
b.
Answer to Problem 43CE
The coefficient of determination is 0.147.
Explanation of Solution
The coefficient of determination is the square of the correlation coefficient. From Part (a), the correlation coefficient is –0.384.
The coefficient of determination is as follows:
The value of coefficient of determination is 0.147. Therefore, 14.7% of variation in the dependent variable is explained by the independent variable.
c.
Test whether there is a negative association between the ‘point scored’ and ‘point allowed’ or not.
c.
Answer to Problem 43CE
There is enough evidence to infer that there is a negative association between the ‘point scored’ and ‘point allowed’.
Explanation of Solution
Denote the population correlation as
The hypotheses are given below:
Null hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is greater than or equal to zero.
Alternative hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is negative.
Test statistic:
The test statistic is as follows:
Here, the
The test statistic is as follows:
The degrees of freedom is as follows:
Thus, the level of significance is 0.05.
Critical value:
Software procedure:
Step-by-step software procedure to obtain the critical value using EXCEL software:
- Open an EXCEL file.
- In cell A1, enter the formula “=T.INV (0.05, 30)”.
Output obtained using the EXCEL is given as follows:
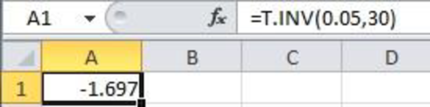
From the EXCEL output, the critical value is –1.697
Decision rule:
Reject the null hypothesis H0, if
Conclusion:
The value of test statistic is –2.28 and the critical value is –1.697.
Here,
By the rejection rule, reject the null hypothesis.
Thus, there is enough evidence to infer that there is a negative association between the ‘point scored’ and ‘point allowed’.
d.
Test whether there is a negative association between the ‘point scored’ and ‘point allowed’ for each conference or not.
d.
Answer to Problem 43CE
There is a negative association between the ‘point scored’ and ‘point allowed’ in conference AFC.
There is no evidence that a negative association between the ‘point scored’ and ‘point allowed’ in conference NFC.
Explanation of Solution
Denote the population correlation as
For conference AFC:
The hypotheses are given below:
Null hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is greater than or equal to zero in conference AFC.
Alternative hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is negative in conference AFC.
Step-by-step procedure to obtain the correlation coefficient using MegaStat software:
- In an EXCEL sheet enter the data values of x and y.
- Go to Add-Ins > MegaStat > Correlation/Regression > Correlation matrix.
- Enter Input Range as $A$1:$B$17.
- Click on OK.
Output obtained using MegaStat is given as follows:
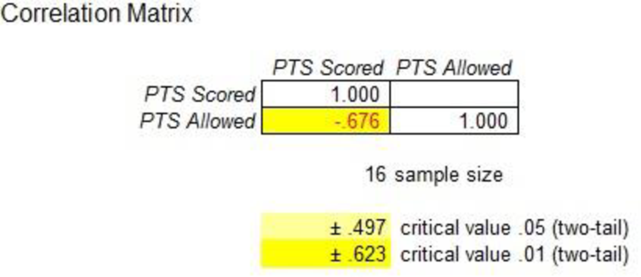
Test statistic:
The test statistic is as follows:
Here, the sample size is 16 and the correlation coefficient is –0.676.
The test statistic is as follows:
The degrees of freedom is as follows:
The level of significance is 0.05.
Critical value:
Software procedure:
Step-by-step software procedure to obtain the critical value using EXCEL software:
- Open an EXCEL file.
- In cell A1, enter the formula “=T.INV (0.05, 14)”.
Output obtained using EXCEL is given as follows:
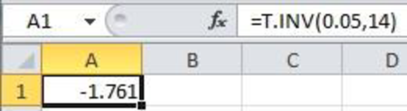
From the EXCEL output, the critical value is –1.761
Decision rule:
Reject the null hypothesis H0, if
Conclusion:
The value of test statistic is –3.432 and the critical value is –1.761.
Here,
By the rejection rule, reject the null hypothesis.
Thus, there is enough evidence to infer that there is a negative association between the ‘point scored’ and ‘point allowed’ in conference AFC.
For conference NFC:
The hypotheses are given below:
Null hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is greater than or equal to zero in conference NFC.
Alternative hypothesis:
That is, the correlation between ‘point scored’ and ‘point allowed’ is a negative in conference NFC.
Step-by-step procedure to obtain the correlation coefficient using MegaStat software:
- In an EXCEL sheet enter the data values of x and y.
- Go to Add-Ins > MegaStat > Correlation/Regression > Correlation matrix.
- Enter Input Range as $A$1:$B$17.
- Click on OK.
Output obtained using MegaStat is given as follows:
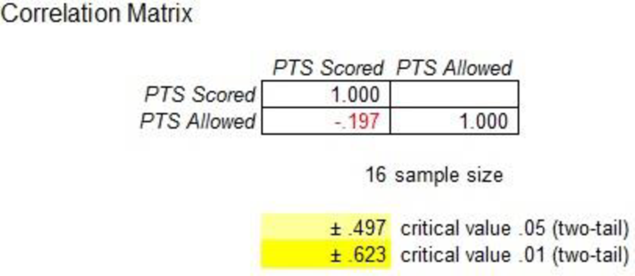
Test statistic:
The test statistic is as follows:
Here, the sample size is 16 and the correlation coefficient is –0.197.
The test statistic is as follows:
Conclusion:
The value of test statistic is –0.752 and the critical value is –1.761.
Here,
By the rejection rule, fail to reject the null hypothesis.
Thus, there is no enough evidence to infer that there is a negative association between the ‘point scored’ and ‘point allowed’ in conference NFC.
Want to see more full solutions like this?
Chapter 13 Solutions
Gen Combo Ll Statistical Techniques In Business And Economics; Connect Ac
- Business discussarrow_forwardBusiness discussarrow_forwardI just need to know why this is wrong below: What is the test statistic W? W=5 (incorrect) and What is the p-value of this test? (p-value < 0.001-- incorrect) Use the Wilcoxon signed rank test to test the hypothesis that the median number of pages in the statistics books in the library from which the sample was taken is 400. A sample of 12 statistics books have the following numbers of pages pages 127 217 486 132 397 297 396 327 292 256 358 272 What is the sum of the negative ranks (W-)? 75 What is the sum of the positive ranks (W+)? 5What type of test is this? two tailedWhat is the test statistic W? 5 These are the critical values for a 1-tailed Wilcoxon Signed Rank test for n=12 Alpha Level 0.001 0.005 0.01 0.025 0.05 0.1 0.2 Critical Value 75 70 68 64 60 56 50 What is the p-value for this test? p-value < 0.001arrow_forward
- ons 12. A sociologist hypothesizes that the crime rate is higher in areas with higher poverty rate and lower median income. She col- lects data on the crime rate (crimes per 100,000 residents), the poverty rate (in %), and the median income (in $1,000s) from 41 New England cities. A portion of the regression results is shown in the following table. Standard Coefficients error t stat p-value Intercept -301.62 549.71 -0.55 0.5864 Poverty 53.16 14.22 3.74 0.0006 Income 4.95 8.26 0.60 0.5526 a. b. Are the signs as expected on the slope coefficients? Predict the crime rate in an area with a poverty rate of 20% and a median income of $50,000. 3. Using data from 50 workarrow_forward2. The owner of several used-car dealerships believes that the selling price of a used car can best be predicted using the car's age. He uses data on the recent selling price (in $) and age of 20 used sedans to estimate Price = Po + B₁Age + ε. A portion of the regression results is shown in the accompanying table. Standard Coefficients Intercept 21187.94 Error 733.42 t Stat p-value 28.89 1.56E-16 Age -1208.25 128.95 -9.37 2.41E-08 a. What is the estimate for B₁? Interpret this value. b. What is the sample regression equation? C. Predict the selling price of a 5-year-old sedan.arrow_forwardian income of $50,000. erty rate of 13. Using data from 50 workers, a researcher estimates Wage = Bo+B,Education + B₂Experience + B3Age+e, where Wage is the hourly wage rate and Education, Experience, and Age are the years of higher education, the years of experience, and the age of the worker, respectively. A portion of the regression results is shown in the following table. ni ogolloo bash 1 Standard Coefficients error t stat p-value Intercept 7.87 4.09 1.93 0.0603 Education 1.44 0.34 4.24 0.0001 Experience 0.45 0.14 3.16 0.0028 Age -0.01 0.08 -0.14 0.8920 a. Interpret the estimated coefficients for Education and Experience. b. Predict the hourly wage rate for a 30-year-old worker with four years of higher education and three years of experience.arrow_forward
- 1. If a firm spends more on advertising, is it likely to increase sales? Data on annual sales (in $100,000s) and advertising expenditures (in $10,000s) were collected for 20 firms in order to estimate the model Sales = Po + B₁Advertising + ε. A portion of the regression results is shown in the accompanying table. Intercept Advertising Standard Coefficients Error t Stat p-value -7.42 1.46 -5.09 7.66E-05 0.42 0.05 8.70 7.26E-08 a. Interpret the estimated slope coefficient. b. What is the sample regression equation? C. Predict the sales for a firm that spends $500,000 annually on advertising.arrow_forwardCan you help me solve problem 38 with steps im stuck.arrow_forwardHow do the samples hold up to the efficiency test? What percentages of the samples pass or fail the test? What would be the likelihood of having the following specific number of efficiency test failures in the next 300 processors tested? 1 failures, 5 failures, 10 failures and 20 failures.arrow_forward
- The battery temperatures are a major concern for us. Can you analyze and describe the sample data? What are the average and median temperatures? How much variability is there in the temperatures? Is there anything that stands out? Our engineers’ assumption is that the temperature data is normally distributed. If that is the case, what would be the likelihood that the Safety Zone temperature will exceed 5.15 degrees? What is the probability that the Safety Zone temperature will be less than 4.65 degrees? What is the actual percentage of samples that exceed 5.25 degrees or are less than 4.75 degrees? Is the manufacturing process producing units with stable Safety Zone temperatures? Can you check if there are any apparent changes in the temperature pattern? Are there any outliers? A closer look at the Z-scores should help you in this regard.arrow_forwardNeed help pleasearrow_forwardPlease conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. 4. One-Way ANOVA: Analyze the customer satisfaction scores across four different product categories to determine if there is a significant difference in means. (Hints: The null can be about maintaining status-quo or no difference among groups) H0 = H1=arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL


