Concept explainers
Videos
a.
To calculate: The probability that the outcome will be between $16,800 and $31,200.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
a.
Answer to Problem 20P
The probability that the outcome will be between $16,800 and $31,200 is 0.8664.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being equal to or greater than $16,800 is shown below.
The calculation of the expected value (Z) for the outcome being equal to or lower than $31,200 is shown below.
The Z values are positive as well as negative 1.5. Hence, the probability of the outcome being between $16,800 and $31,200 is 0.8664.
b.
To calculate: The probability that the outcome will be between $14,400 and $33,600.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
b.
Answer to Problem 20P
The probability that the outcome will be between $14,400 and $33,600 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being equal to or greater than $14,400 is shown below.
The calculation of the expected value (Z) for the outcome being equal to or lower than $33,600 is shown below.
The Z values are positive as well as negative 2. Hence, the probability of the outcome being between $14,400 and $33,600 is 0.9544.
c.
To calculate: The probability that the outcome will be at least $14,400.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
c.
Answer to Problem 20P
The probability that the outcome will be at least $14,400 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being at least $14,400 is shown below.
The expected value is 0.4772 when Z is (+ or -) 2 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.9772. The graph of this probability is shown below.
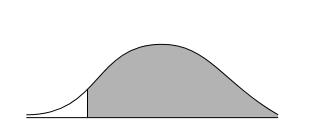
d.
To calculate: The probability that the outcome will be less than $31,900.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
d.
Answer to Problem 20P
The probability that the outcome will be less than $31,900 is 0.9544.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being at least $14,400 is shown below.
The expected value is 0.4505 when Z is (+ or -) 1.65 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.9505. The graph of this probability is shown below.
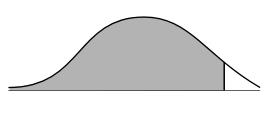
e.
To calculate: The probability that the outcome will be less than $19,200 or greater than $26,400.
Introduction:
Probability:
The likelihood of the occurrence of an event or of a proposition to be true, when expressed numerically or quantitatively, is termed as probability.
e.
Answer to Problem 20P
The probability that the outcome will be less than $19,200 or greater than $26,400 is 0.4672.
Explanation of Solution
The calculation of the expected value (Z) for the outcome being less than $19,200 is shown below.
The expected value is 0.3413 when Z is (+ or -) 1 and 0.5000 when Z is 0. So, the probability of the outcome being less than $19,200 is 0.1587 (0.5000 – 0.3413).
The calculation of the expected value (Z) for the outcome being greater than $26,400 is shown below.
The expected value is 0.1915 when Z is (+ or -) 1 and 0.5000 when Z is 0. So, the probability of the outcome being at least $14,400 is 0.3085 (0.5000 – 0.1915).
Hence, the probability that the outcome will be less than $19,200 or greater than $26,400 is 0.4672. The graph of this probability is shown below.
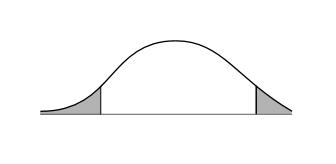
Want to see more full solutions like this?
Chapter 13 Solutions
FOUND.OF FINANCIAL MANAGEMENT-ACCESS
- Don't used Ai solutionarrow_forwardllumina Inc. is expected to pay its next dividend of $0.4 two years from now. This dividend should then grow at a rate of 10% for 3 years (till the end of year 5), and at a reduced rate of 6% thereafter. The market required rate of return is 16%. The price of the company's shares today is: $4.15 $4.39 $3.79 $3.96arrow_forwardA bank has made a loan charging a base lending rate of 8%. It expects a probability of default of 5%. If the loan is defaulted, it expects to recover 50% of its money through the sale of its collateral. The expected return on this loan is _____% (rounded to two decimal places).arrow_forward
- Ch 26: Assignment - Mergers and Corporate Control Widget Corp., which is considering the acquisition of Exteter Enterprise Inc., estimates that acquiring Exteter will result in an incremental value for the firm. The analysts involved in the deal have collected the following information from the projected financial statements of the target company: Data Collected (in millions of dollars) Year 1 Year 2 Year 3 EBIT $13.0 $15.6 $19.5 Interest expense 5.0 5.5 6.0 Debt 35.2 41.6 44.8 Total net operating capital 107.1 109.2 111.3 Exteter Enterprise Inc. is a publicly traded company, and its market-determined pre-merger beta is 1.00. You also have the following information about the company and the projected statements: •Exteter currently has a $38.00 million market value of equity and $24.70 million in debt. The risk-free rate is 3.5%, there is a 5.60% market risk premium, and the Capital Asset Pricing Model produces a pre-merger required rate of return on equity ISL of 9.10%. •Exteter's cost…arrow_forward3. Problem 30-03 (Plan Funding) Plan Funding eBook Consolidated Industries is planning to operate for 10 more years and then cease operations. At that time (in 10 years), it expects to have the following pension benefit obligations: Year 11-15 16-20 21-25 Annual Total Payment $3,480,000 2,980,000 26-30 31-35 2,480,000 1,980,000 1,480,000 The current value of the firm's pension fund is $5.6 million. Assume that all cash flows occur at year-end. a. Consolidated's expected return on pension assets is 11%, and it uses 11% to discount the expected pension benefit payments. What is the present value of the firm's pension fund benefits? Do not round intermediate calculations. Round your answer to the nearest dollar. $ b. Is the plan underfunded or overfunded? Do not round intermediate calculations. Round your answer to two decimal places. Funding ratio= which means the assets are select than the PV of benefits and the plan is select Less or greater Select underfunded overfundedarrow_forwardPlan Funding Consolidated Industries is planning to operate for 10 more years and then cease operations. At that time (in 10 years), it expects to have the following pension benefit obligations: Year 11-15 16-20 21-25 Annual Total Payment $3,500,000 3,000,000 2,500,000 26-30 31-35 2,000,000 1,500,000 The current value of the firm's pension fund is $6.1 million. Assume that all cash flows occur at year-end. a. Consolidated's expected return on pension assets is 12%, and it uses 12% to discount the expected pension benefit payments. What is the present value of the firm's pension fund benefits? Do not round intermediate calculations. Round your answer to the nearest dollar. $ b. Is the plan underfunded or overfunded? Do not round intermediate calculations. Round your answer to two decimal places. Funding ratio = which means the assets are -Select- than the PV of benefits and the plan is -Select- ☑. Less or Greater Overfunded or Underfundedarrow_forward
- Benefits and Contributions The Certainty Company (CC) operates in a world of certainty. It has just hired Mr. Jones, age 27, who will retire at age 65, draw retirement benefits for 14 years, and die at age 79. Mr. Jones' salary is $21,000 per year, but wages are expected to increase at the 6% annual rate of inflation. CC has a defined benefit plan in which workers receive 1% of the final year's wage for each year employed. The retirement benefit, once started, does not have a cost-of-living adjustment. CC earns 12% annually on its pension fund assets and uses a 10% rate to discount its expected future benefit payments. Assume that pension contribution and benefit cash flows occur at year-end. Do not round intermediate calculations. Round your answers to the nearest dollar. a. How much will Mr. Jones receive in annual retirement benefits? $ b. What is CC's required annual contribution to fully fund Mr. Jones' retirement benefits? $ c. Assume now that CC hires Mr. Smith at the same…arrow_forwardlab.infoseclearning.com/console/5061763/3047 310-win10 Project Three Milestone - GNS3 File Edit View Control Node Annotate Tools Help e 41 Sales_PC1 0000 Sales_PC2 Sales_PC3 Enforce US Keyboard Layout View Fullscreen Send Ctrl+Alt+Delete Reboot To exit full screen, press and hold esc ■C00/6@ Q Sales_Switch Human Resources_Switch Office_Router Sales PC4 Customer_Service_Switch X: -299.0 Y: -136.0 Z: 1.0 H Type here to search CS_FTP_Server HR_PC2 HR_PC1 7:19 PM 12/14/2024 Barrow_forwardAGG is a US multinational that manufactures specialist high tech parts in the airline engine industry. AGG is an established company with steady growth in turnover and dividends over the last 10 years. The company is undertaking a projected titled Project Big as a strategic response to the changing market scene. AGG will develop a new state of the art highly automated plant located in Cambodia which is expected to result in cost advantages if it is implemented. The details about the project are below • Initital investment has been estimated at $500m • • The annual pre tax savings in operating costs at current exchange rates has been calculated at $150m for the first four years (starting in the first year) The residual value of the project at the end of the four years is estimated to be $250m The initial investment, net of residual value, qualifies for capital allowance and can be claimed back on a straight line basis over the four years of the project. Current AGG's cost of capital is…arrow_forward
- You have just won the Strayer Lottery jackpot of $11,000,000. You will be paid in twenty-six equal annual installments beginning immediately. If you had the money now, you could invest it in an account with a quoted annual interest rate of 9% with monthly compounding of interest. Calculate the present value of the payments you will receive. Show your calculations using formulas in your paper or provide how to do the calculations in Excel. Explain why there is a difference between the present value of the Strayer lottery jackpot and the future value of the twenty-six annual payments based on your calculations and the information provided.arrow_forwardYou have just won the Strayer Lottery jackpot of $11,000,000. You will be paid in twenty-six equal annual installments beginning immediately. If you had the money now, you could invest it in an account with a quoted annual interest rate of 9% with monthly compounding of interest. Calculate the present value of the payments you will receive. Show your calculations using formulas in your paper or in an attached spreadsheet file.arrow_forwardThe approach uses a weighted average cost of capital that is unique to a particular project while determining the appropriate discount rate.arrow_forward
Essentials of Business Analytics (MindTap Course ...StatisticsISBN:9781305627734Author:Jeffrey D. Camm, James J. Cochran, Michael J. Fry, Jeffrey W. Ohlmann, David R. AndersonPublisher:Cengage Learning