Chapter 13, Problem 13.84E

Interpretation Introduction

Interpretation:

The $O_{\text{h}}$ symmetry species of the $s{p}^3{d}^2$ hybrid orbitals, with the assumption that the hybrid orbitals are all coincident with the Cartesian axes is to be predicted.

Concept introduction:

The characters of the irreducible representations of the given point group can be multiplied by each other. The only condition is that the characters of the same symmetry operations are multiplied together. The multiplication of the characters is commutative.

The great orthogonality theorem for the reducible representation can be represented as,

$a_{\Gamma }=& \frac{1}{h}{\displaystyle \sum _{\begin{array}{l}\text{all}\text{classes}\\ \text{of}\text{point}\text{group}\end{array}}N\cdot {\chi }_{\Gamma }\cdot {\chi }_{\text{linear}\text{combo}}}$

Where,

• $a_{\Gamma }$ is the number of times the irreducible representation appears in a linear combination.

• $h$ is the order of the group.

• ${\chi }_{\Gamma }$ is the character of the class of the irreducible representation.

• ${\chi }_{\text{linear}\text{combo}}$ is the character of the class linear combination.

• $N$ is the number of symmetry operations.

Answer to Problem 13.84E

The $O_{\text{h}}$ symmetry species of the $s{p}^3{d}^2$ hybrid orbitals, with the assumption that the hybrid orbitals are all coincident with the Cartesian axes is $A_{1g}\oplus E_g\oplus T_{\text{1u}}$.

Explanation of Solution

The symmetry elements present in octahedral symmetry are, $E$, $C_3$, $C_2$, $C_4$, $C_2\text{'}$, $i$, $S_4$, $S_6$, ${\sigma }_{\text{h}}$ and ${\sigma }_{\text{d}}$. The $s{p}^3{d}^2$ hybrid orbitals can be represented as,

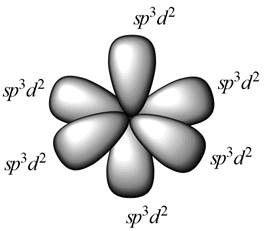
Figure 1

For the symmetry element $E$ each hybrid orbital operates onto itself and contributes character $+6$. For $C_3$ symmetry element in $s{p}^3{d}^2$ hybrid orbitals,

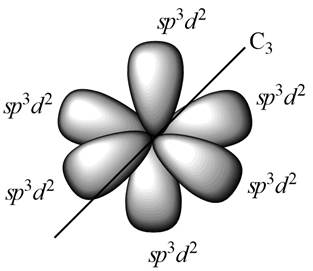
Figure 2

All the $s{p}^3{d}^2$ hybrid orbitals exchange their positions such that ${\chi }_{C_3}=& 0$.

For $C_2$ symmetry element in $s{p}^3{d}^2$ hybrid orbitals,

Figure 3

The $C_2$ rotation axis passing through two orbitals gives the contribution as ${\chi }_{C_2}=& 2$ as four orbitals exchange their positions while two orbitals retain their position.

The $C_2$ rotation axis passing between the orbitals gives the contribution as ${\chi }_{C_2}=& 0$ as all the orbitals exchange their positions.

The $C_4$ rotation axis passing through two orbitals gives the contribution as ${\chi }_{C_4}=& 2$ as four orbitals exchange their positions while two orbitals retain their position.

On inversion of the given set of orbitals, all the hybrid orbitals exchange their position and their contribution is ${\chi }_i=& 0$.

For $S_4$ symmetry element first $C_2$ rotation axis is applied and then apply the ${\sigma }_{\text{h}}$ which results in zero contribution.

For $S_6$ symmetry element first $C_3$ rotation axis is applied and then apply the ${\sigma }_{\text{h}}$ which results in zero contribution.

For ${\sigma }_{\text{h}}$, the plane passes through four orbitals and thus, the four orbitals retain their position and two orbitals exchange their position and thus, the contribution is ${\chi }_{{\sigma }_{\text{h}}}=& 4$.

For ${\sigma }_d$, the mirror plane plane passes through two orbitals and thus, the four orbitals exchange their positions and two orbitals retain their position. Thus, the contribution is ${\chi }_{{\sigma }_d}=& 2$.

This plane can be represented as,

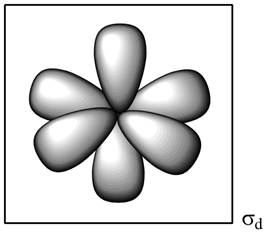
Figure 4

Thus, the reducible representations from the given contribution is,

$\begin{array}{ccccccccccc}{O}_{\text{h}}& E& 8C_3& 3C_2& 6C_4& 6C_2\text{'}& i& 8S_6& 3{\sigma }_{\text{h}}& 6S_4& 6{\sigma }_{\text{d}}\\ & 6& 0& 2& 2& 0& 0& 0& 4& 0& 2\end{array}$

The great orthogonality theorem for the reducible representation can be represented as,

$a_{\Gamma }=& \frac{1}{h}{\displaystyle \sum _{\begin{array}{l}\text{all}\text{classes}\\ \text{of}\text{point}\text{group}\end{array}}N\cdot {\chi }_{\Gamma }\cdot {\chi }_{\text{linear}\text{combo}}}$

Where,

• $a_{\Gamma }$ is the number of times the irreducible representation appears in a linear combination.

• $h$ is the order of the group.

• ${\chi }_{\Gamma }$ is the character of the class of the irreducible representation.

• ${\chi }_{\text{linear}\text{combo}}$ is the character of the class linear combination.

• $N$ is the number of symmetry operations.

The order of the group is $48$.

Substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations for $A_{1g}$.

$\begin{array}{rll}{a}_{{\text{A}}_{1g}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 1\cdot 6\right)+\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 2\right)+\left(6\cdot 1\cdot 2\right)+\left(6\cdot 1\cdot 0\right)+\left(1\cdot 1\cdot 0\right)\\ +\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 4\right)+\left(6\cdot 1\cdot 0\right)+\left(6\cdot 1\cdot 2\right)\end{array}\right]\\ & =& \frac{1}{48}\left[48\right]\\ & =& 1\end{array}$

The number of times the irreducible representation for $A_{1g}$ appears in a linear combination is $1$.

Similarly, for $A_{2g}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{A}}_{2g}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 1\cdot 6\right)+\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 2\right)+\left(6\cdot -1\cdot 2\right)+\left(6\cdot -1\cdot 0\right)+\left(1\cdot 1\cdot 0\right)\\ +\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 4\right)+\left(6\cdot -1\cdot 0\right)+\left(6\cdot -1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $A_{2g}$ appears in a linear combination is $0$.

Similarly, for $E_g$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{E}}_g}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 2\cdot 6\right)+\left(8\cdot -1\cdot 0\right)+\left(3\cdot 2\cdot 2\right)+\left(6\cdot 0\cdot 2\right)+\left(6\cdot 0\cdot 0\right)+\left(1\cdot 2\cdot 0\right)\\ +\left(8\cdot -1\cdot 0\right)+\left(3\cdot 2\cdot 4\right)+\left(6\cdot 0\cdot 0\right)+\left(6\cdot 0\cdot 2\right)\end{array}\right]\\ & =& 1\end{array}$

The number of times the irreducible representation for $E_g$ appears in a linear combination is $1$.

Similarly, for $T_{1g}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{1g}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 3\cdot 6\right)+\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 2\right)+\left(6\cdot 1\cdot 2\right)+\left(6\cdot -1\cdot 0\right)+\left(1\cdot 3\cdot 0\right)\\ +\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 4\right)+\left(6\cdot 1\cdot 0\right)+\left(6\cdot -1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $T_{1g}$ appears in a linear combination is $0$.

Similarly, for $T_{2g}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{2g}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 3\cdot 6\right)+\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 2\right)+\left(6\cdot -1\cdot 2\right)+\left(6\cdot 1\cdot 0\right)+\left(1\cdot 3\cdot 0\right)\\ +\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 4\right)+\left(6\cdot -1\cdot 0\right)+\left(6\cdot 1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $T_{2g}$ appears in a linear combination is $0$.

Similarly, for $A_{\text{1u}}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{A_{1u}}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 1\cdot 6\right)+\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 2\right)+\left(6\cdot 1\cdot 2\right)+\left(6\cdot 1\cdot 0\right)+\left(1\cdot -1\cdot 0\right)\\ +\left(8\cdot -1\cdot 0\right)+\left(3\cdot -1\cdot 4\right)+\left(6\cdot -1\cdot 0\right)+\left(6\cdot -1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $A_{\text{1u}}$ appears in a linear combination is $0$.

Similarly, for $A_{\text{2u}}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{A_{2u}}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 1\cdot 6\right)+\left(8\cdot 1\cdot 0\right)+\left(3\cdot 1\cdot 2\right)+\left(6\cdot -1\cdot 2\right)+\left(6\cdot -1\cdot 0\right)+\left(1\cdot -1\cdot 0\right)\\ +\left(8\cdot -1\cdot 0\right)+\left(3\cdot -1\cdot 4\right)+\left(6\cdot 1\cdot 0\right)+\left(6\cdot 1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $A_{\text{2u}}$ appears in a linear combination is $0$.

Similarly, for $E_{\text{u}}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{E}}_u}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 2\cdot 6\right)+\left(8\cdot -1\cdot 0\right)+\left(3\cdot 2\cdot 2\right)+\left(6\cdot 0\cdot 2\right)+\left(6\cdot 0\cdot 0\right)+\left(1\cdot -2\cdot 0\right)\\ +\left(8\cdot 1\cdot 0\right)+\left(3\cdot -2\cdot 4\right)+\left(6\cdot 0\cdot 0\right)+\left(6\cdot 0\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $E_{\text{u}}$ appears in a linear combination is $0$.

Similarly, for $T_{\text{1u}}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{1u}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 3\cdot 6\right)+\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 2\right)+\left(6\cdot 1\cdot 2\right)+\left(6\cdot -1\cdot 0\right)+\left(1\cdot -3\cdot 0\right)\\ +\left(8\cdot 0\cdot 0\right)+\left(3\cdot 1\cdot 4\right)+\left(6\cdot -1\cdot 0\right)+\left(6\cdot 1\cdot 2\right)\end{array}\right]\\ & =& \frac{1}{48}\left[48\right]\\ & =& 1\end{array}$

The number of times the irreducible representation for $T_{\text{1u}}$ appears in a linear combination is $1$.

Similarly, for $T_{\text{2u}}$, substitute the value of order of the group, character of the class of the irreducible representation from character table of $O_{\text{h}}$ point group, character of the class linear combination and number of symmetry operations.

$\begin{array}{rll}{a}_{{\text{T}}_{1u}}& =& \frac{1}{48}\left[\begin{array}{l}\left(1\cdot 3\cdot 6\right)+\left(8\cdot 0\cdot 0\right)+\left(3\cdot -1\cdot 2\right)+\left(6\cdot -1\cdot 2\right)+\left(6\cdot 1\cdot 0\right)+\left(1\cdot -3\cdot 0\right)\\ +\left(8\cdot 0\cdot 0\right)+\left(3\cdot 1\cdot 4\right)+\left(6\cdot 1\cdot 0\right)+\left(6\cdot -1\cdot 2\right)\end{array}\right]\\ & =& 0\end{array}$

The number of times the irreducible representation for $T_{\text{2u}}$ appears in a linear combination is $0$.

Thus, the linear combination is $A_{1g}\oplus E_g\oplus T_{\text{1u}}$.

Conclusion

The $O_{\text{h}}$ symmetry species of the $s{p}^3{d}^2$ hybrid orbitals, with the assumption that the hybrid orbitals are all coincident with the Cartesian axes is $A_{1g}\oplus E_g\oplus T_{\text{1u}}$.