University Physics (14th Edition)
14th Edition
ISBN: 9780133969290
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 13.81CP
CALC Mass M is distributed uniformly over a disk of radius a. Find the gravitational force (magnitude and direction) between this disk-shaped mass and a particle with mass m located a distance x above the center of the disk (Fig. P13.81). Does your result reduce to the correct expression as x becomes very large? (Hint: Divide the disk into infinitesimally thin concentric rings, use the expression derived in Exercise 13.35 for the gravitational force due to each ring, and integrate to find the total force.)
Figure P13.81
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1. A charge of -25 μC is distributed uniformly throughout a spherical volume of radius 11.5 cm.
Determine the electric field due to this charge at a distance of (a) 2 cm, (b) 4.6 cm, and (c) 25 cm from
the center of the sphere.
(a) =
=
(b) E =
(c)Ẻ =
=
NC NC NC
1.
A long silver rod of radius 3.5 cm has a charge of -3.9
ис
on its surface. Here ŕ is a unit vector
ст
directed perpendicularly away from the axis of the rod as shown in the figure.
(a) Find the electric field at a point 5 cm from the center of the rod (an outside point).
E =
N
C
(b) Find the electric field at a point 1.8 cm from the center of the rod (an inside point)
E=0
Think & Prepare
N
C
1. Is there a symmetry in the charge distribution? What kind of symmetry?
2. The problem gives the charge per unit length 1. How do you figure out the surface charge density σ
from a?
1. Determine the electric flux through each surface whose cross-section is shown below.
55
S₂
-29
S5
SA
S3
+ 9
Enter your answer in terms of q and ε
Φ
(a) s₁
(b) s₂
=
-29
(C) Φ
զ
Ερ
(d) SA
=
(e) $5
(f) Sa
$6
=
II
✓
-29
S6
+39
Chapter 13 Solutions
University Physics (14th Edition)
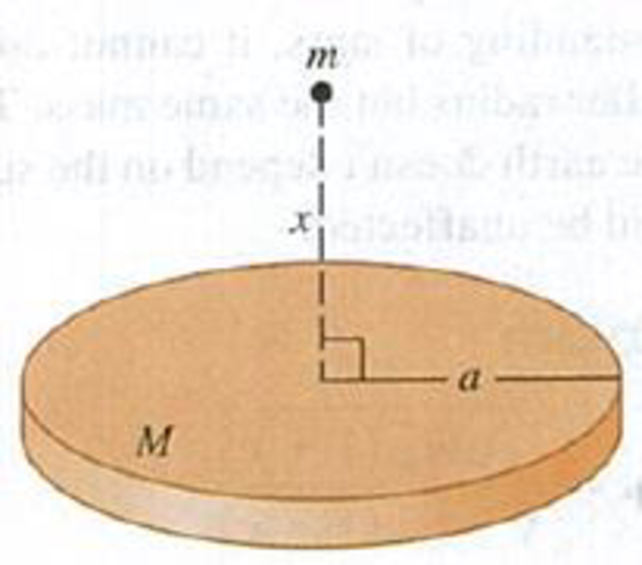
Ch. 13 - A student wrote: The only reason an apple falls...Ch. 13 - If all planets had the same average density, how...Ch. 13 - Is a pound of butler on the earth the same amount...Ch. 13 - Example 13.2 (Section 13.1) shows that the...Ch. 13 - When will you attract the sun more: today at noon,...Ch. 13 - Since the moon is constantly attracted toward the...Ch. 13 - Prob. Q13.7DQCh. 13 - A planet makes a circular orbit with period T...Ch. 13 - The sun pulls on the moon with a force that is...Ch. 13 - Which takes more fuel: a voyage from the earth to...
Ch. 13 - Prob. Q13.11DQCh. 13 - Does the escape speed for an object at the earths...Ch. 13 - If a projectile is fired straight up from the...Ch. 13 - Discuss whether this statement is correct: In the...Ch. 13 - The earth is closer to the sun in November than in...Ch. 13 - A communications firm wants to place a satellite...Ch. 13 - Prob. Q13.17DQCh. 13 - What would Keplers third law be for circular...Ch. 13 - In the elliptical orbit of Comet Hailey shown in...Ch. 13 - Many people believe that orbiting astronauts feel...Ch. 13 - As part of their training before going into orbit,...Ch. 13 - What is the ratio of the gravitational pull of the...Ch. 13 - CP Cavendish Experiment. In the Cavendish balance...Ch. 13 - Rendezvous in Space! A couple of astronauts agree...Ch. 13 - Two uniform spheres, each with mass M and radius...Ch. 13 - Two uniform spheres, each of mass 0.260 kg, are...Ch. 13 - Find the magnitude and direction of the net...Ch. 13 - A typical adult human has a mass of about 70 kg....Ch. 13 - An 8.00-kg point mass and a 12.0-kg point mass are...Ch. 13 - Prob. 13.9ECh. 13 - The point masses m and 2m lie along the x-axis,...Ch. 13 - At what distance above the surface of the earth is...Ch. 13 - The mass of Venus is 81.5% that of the earth, and...Ch. 13 - Prob. 13.13ECh. 13 - Rhea, one of Saturns moons, has a radius of 764 km...Ch. 13 - Calculate the earths gravity force on a 75-kg...Ch. 13 - Prob. 13.16ECh. 13 - Use the results of Example 13.5 (Section 13.3) to...Ch. 13 - Ten days after it was launched toward Mars in...Ch. 13 - A planet orbiting a distant star has radius 3.24 ...Ch. 13 - Prob. 13.20ECh. 13 - Prob. 13.21ECh. 13 - Aura Mission. On July 15, 2004, NASA launched the...Ch. 13 - Two satellites are in circular orbits around a...Ch. 13 - International Space Station. In its orbit each...Ch. 13 - Prob. 13.25ECh. 13 - Prob. 13.26ECh. 13 - The star Rho1 Cancri is 57 light-years from the...Ch. 13 - In March 2006. two small satellites were...Ch. 13 - The dwarf planet Pluto has an elliptical orbit...Ch. 13 - Hot Jupiters. In 2004 astronomers reported the...Ch. 13 - Planets Beyond the Solar System. On October 15,...Ch. 13 - A uniform, spherical, 1000.0-kg shell has a radius...Ch. 13 - A uniform, solid, 1000.0-kg sphere has a radius of...Ch. 13 - CALC A thin, uniform rod has length L and mass M....Ch. 13 - Prob. 13.35ECh. 13 - A Visit to Santa. You decide to visit Santa Claus...Ch. 13 - The acceleration due to gravity at the north pole...Ch. 13 - Mini Black Holes. Cosmologists have speculated...Ch. 13 - Prob. 13.39ECh. 13 - In 2005 astronomers announced the discovery of a...Ch. 13 - Neutron stars, such as the one at the center of...Ch. 13 - Four identical masses of 8.00 kg each are placed...Ch. 13 - Three uniform spheres are fixed at the positions...Ch. 13 - CP Exploring Europa. There is strong evidence that...Ch. 13 - A uniform sphere with mass 50.0 kg is held with...Ch. 13 - Mission to Titan. On December 25, 2004, the...Ch. 13 - Prob. 13.47PCh. 13 - At a certain instant, the earth, the moon, and a...Ch. 13 - Prob. 13.49PCh. 13 - CP Submarines on Europa. Some scientists are eager...Ch. 13 - What is the escape speed from a 300-km-diameter...Ch. 13 - A landing craft with mass 12,500 kg is in a...Ch. 13 - Planet X rotates in the same manner as the earth,...Ch. 13 - (a) Suppose you are at the earths equator and...Ch. 13 - CP An astronaut, whose mission is to go where no...Ch. 13 - CP Your starship, the Aimless Wanderer, lands on...Ch. 13 - CP You are exploring a distant planet. When your...Ch. 13 - The 0.100-kg sphere in Fig. P13.58 is released...Ch. 13 - An unmanned spacecraft is in a circular orbit...Ch. 13 - Mass of a Comet. On July 4, 2005, the NASA...Ch. 13 - Falling Hammer. A hammer with mass m is dropped...Ch. 13 - Prob. 13.62PCh. 13 - Prob. 13.63PCh. 13 - Prob. 13.64PCh. 13 - Prob. 13.65PCh. 13 - The planet Uranus has a radius of 25,360 km and a...Ch. 13 - Prob. 13.67PCh. 13 - A rocket with mass 5.00 103 kg is in a circular...Ch. 13 - A 5000-kg spacecraft is in a circular orbit 2000...Ch. 13 - Prob. 13.70PCh. 13 - CALC Planets are not uniform inside. Normally,...Ch. 13 - One of the brightest comets of the 20th century...Ch. 13 - CALC An object in the shape of a thin ring has...Ch. 13 - CALC A uniform wire with mass M and length L is...Ch. 13 - Prob. 13.75PCh. 13 - DATA For each of the eight planets Mercury to...Ch. 13 - DATA For a spherical planet with mass M, volume V,...Ch. 13 - DATA For a planet in our solar system, assume that...Ch. 13 - CHALLENGE PROBLEMS 13.79Interplanetary Navigation....Ch. 13 - CP Tidal Forces near a Black Hole. An astronaut...Ch. 13 - CALC Mass M is distributed uniformly over a disk...Ch. 13 - EXOPLANETS. As planets with a wide variety of...Ch. 13 - EXOPLANETS. As planets with a wide variety of...Ch. 13 - EXOPLANETS. As planets with a wide variety of...
Additional Science Textbook Solutions
Find more solutions based on key concepts
11. A ball of putty is dropped from a height of 2 m onto a hard floor, where it sticks. What object or objects ...
College Physics: A Strategic Approach (3rd Edition)
2. Define equilibrium population. Outline the conditions that must be met for a population to stay in genetic e...
Biology: Life on Earth (11th Edition)
Fibrous connective tissue consists of ground substance and fibers that provide strength, support, and flexibili...
Human Biology: Concepts and Current Issues (8th Edition)
2. Whether an allele is dominant or recessive depends on
a. how common the allele is, relative to other alleles...
Campbell Biology: Concepts & Connections (9th Edition)
If someone at the other end of a room smokes a cigarette, you may breathe in some smoke. The movement of smoke ...
Campbell Essential Biology with Physiology (5th Edition)
A mixed culture of Escherichia coli and Penicillium chrysogenum is inoculated onto the following culture media....
Microbiology: An Introduction
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwardthe cable may break and cause severe injury. cable is more likely to break as compared to the [1] ds, inclined at angles of 30° and 50° to the vertical rings by way of a scaled diagram. [4] I 30° T₁ 3cm 3.8T2 cm 200 N 50° at it is headed due North and its airspeed indicat 240 km/h. If there is a wind of 100 km/h from We e relative to the Earth? [3]arrow_forwardCan you explain this using nodal analysis With the nodes I have present And then show me how many KCL equations I need to write, I’m thinking 2 since we have 2 dependent sourcesarrow_forward
- The shear leg derrick is used to haul the 200-kg net of fish onto the dock as shown in. Assume the force in each leg acts along its axis. 5.6 m. 4 m- B Part A Determine the compressive force along leg AB. Express your answer to three significant figures and include the appropriate units. FAB = Value Submit Request Answer Part B Units ? Determine the compressive force along leg CB. Express your answer to three significant figures and include the appropriate units. FCB= Value Submit Request Answer Part C ? Units Determine the tension in the winch cable DB. Express your answer with the appropriate units. 2marrow_forwardPart A (Figure 1) shows a bucket suspended from a cable by means of a small pulley at C. If the bucket and its contents have a mass of 10 kg, determine the location of the pulley for equilibrium. The cable is 6 m long. Express your answer to three significant figures and include the appropriate units. Figure 4 m B НА x = Value Submit Request Answer Provide Feedback < 1 of 1 T 1 m Units ?arrow_forwardThe particle in is in equilibrium and F4 = 165 lb. Part A Determine the magnitude of F1. Express your answer in pounds to three significant figures. ΑΣΦ tvec F₁ = Submit Request Answer Part B Determine the magnitude of F2. Express your answer in pounds to three significant figures. ΑΣΦ It vec F2 = Submit Request Answer Part C Determine the magnitude of F3. Express your answer in pounds to three significant figures. ? ? lb lb F₂ 225 lb 135° 45° 30° -60°-arrow_forward
- The 10-lb weight is supported by the cord AC and roller and by the spring that has a stiffness of k = 10 lb/in. and an unstretched length of 12 in. as shown in. Part A Determine the distance d to maintain equilibrium. Express your answer in inches to three significant figures. 節 ΕΠΙ ΑΣΦ d = *k J vec 5 t 0 ? d C A in. 12 in. Barrow_forwardThe members of a truss are connected to the gusset plate as shown in . The forces are concurrent at point O. Take = 90° and T₁ = 7.5 kN. Part A Determine the magnitude of F for equilibrium. Express your answer to three significant figures and include the appropriate units. F = Value Submit Request Answer Part B 0 ? Units Determine the magnitude of T2 for equilibrium. Express your answer to three significant figures and include the appropriate units. ? T₂ = Value Units T₁ Carrow_forwardpls help on botharrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY