Chapter 13, Problem 13.34P

(a)

Interpretation Introduction

Interpretation:

The parameter values for the Margules equation which provide the best fit of $G^E/RT$to the given data are to be determined. Also, a $P-x-y$diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

The formula to calculate the value of $G^E/RT$for a binary system is:

  $\frac{G^E}{RT}=x_1\ln {\gamma }_1+x_2\ln {\gamma }_2$   ...... (2)

Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=\left(A_{12}{x}_1+A_{21}{x}_2\right)x_1{x}_2$   ...... (3)

Here, $A_{12}\text{ and }{A}_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$are:

  $\begin{array}{c}\ln {\gamma }_1=x_2^2\left[A_{12}+2\left(A_{21}-A_{12}\right)x_1\right]\\ \ln {\gamma }_2=x_1^2\left[A_{21}+2\left(A_{12}-A_{21}\right)x_2\right]\end{array}$   ...... (4)

Answer to Problem 13.34P

The parameter values for the Margules equation which provide the best fit of $G^E/RT$to the given data are:

  $\begin{array}{c}{A}_{12}=0.7077\\ A_{21}=0.6897\end{array}$

The $P-x-y$diagram for the binary system containing methanol(1)/water(2) at ${\text{55}}^{\circ }\text{C}$for both calculated as well as experimental values are shown below. The values do not deviate by considerable extent from each other.

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol (1)/water (2) at ${\text{55}}^{\circ }\text{C}$is:

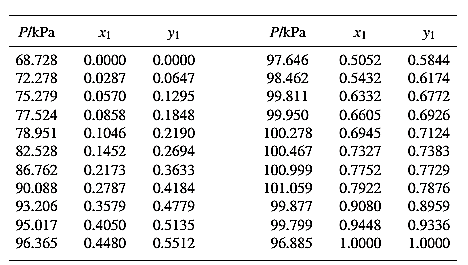
From the given data, first calculate the value of $x_2,\text{ and }{y}_2$and tabulating them in excel spreadsheet as shown below:

Now, use equation (1) for the Modifies Raoult’s law and calculate the value of ${\gamma }_1\text{ and }{\gamma }_2$using the below mentioned formula and tabulate it in the excel spreadsheet.

  $\begin{array}{c}{\gamma }_1=\frac{y_{1}P}{x_1{P}_1{}^{\text{sat}}}\\ {\gamma }_2=\frac{y_{2}P}{x_2{P}_2{}^{\text{sat}}}\end{array}$

Use the equation (2) to calculate the value of $G^E/RT$for every value of $x_1$and tabulate it in the excel spreadsheet as shown below:

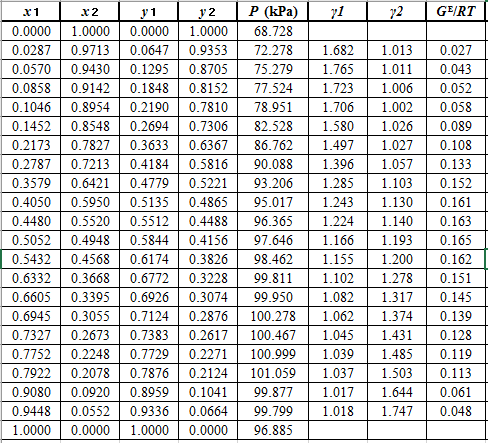
Rewrite equation (3) so that the equation becomes linear in $x_1$as:

  $\begin{array}{c}\left(\frac{G^E/RT}{x_1{x}_2}\right)=\left(A_{12}{x}_1+A_{21}\left(1-x_1\right)\right)\\ \left(\frac{G^E/RT}{x_1{x}_2}\right)=\left(A_{21}-A_{12}\right)x_1+A_{12}\mathrm{......}\text{ (5)}\end{array}$

Now, calculate the values of $\left(\frac{G^E/RT}{x_1{x}_2}\right)$as shown below:

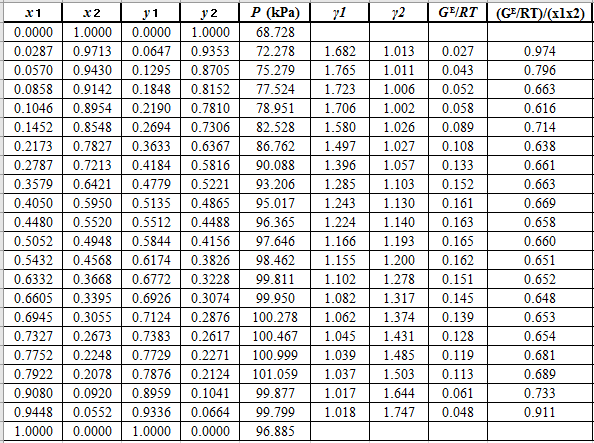
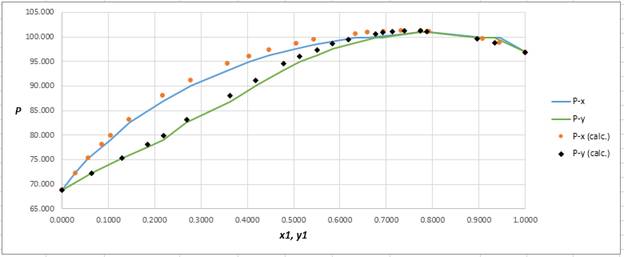
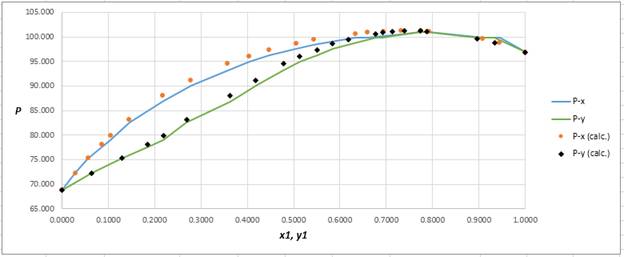
Plot the graph of $\left(\frac{G^E/RT}{x_1{x}_2}\right)$versus $x_1$and using the excel toolas:

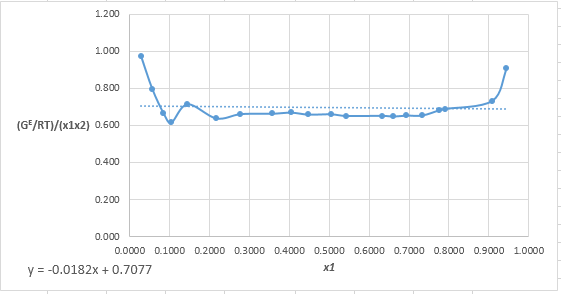
The equation that fits the plot is:

  $\left(\frac{G^E/RT}{x_1{x}_2}\right)=-0.0182x_1+0.7077$

Compare it with equation (5) so that the values of $A_{12}\text{ and }{A}_{21}$will be:

  $\begin{array}{c}{A}_{12}=0.7077\\ A_{21}=0.6897\end{array}$

According to the above correlation for $G^E/RT$and the values of $A_{12}\text{ and }{A}_{21}$, the correlations for $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$using the equation set (4) will be:

  $\begin{array}{c}\ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=x_2^2\left[A_{12}+2\left(A_{21}-A_{12}\right)x_1\right]\\ \ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=x_2^2\left[0.7077+2\left(0.6897-0.7077\right)x_1\right]\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left(x_2^2\left[0.7077-0.036x_1\right]\right)\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=x_1^2\left[A_{21}+2\left(A_{12}-A_{21}\right)x_2\right]\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=x_1^2\left[0.6897+2\left(0.7077-0.6897\right)x_2\right]\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left(x_1^2\left[0.6897+0.036x_2\right]\right)\end{array}$

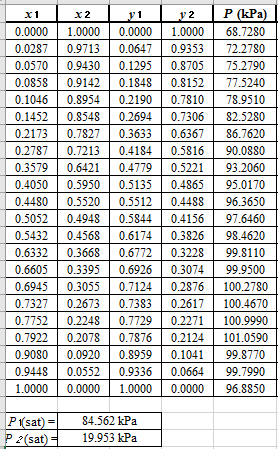
Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

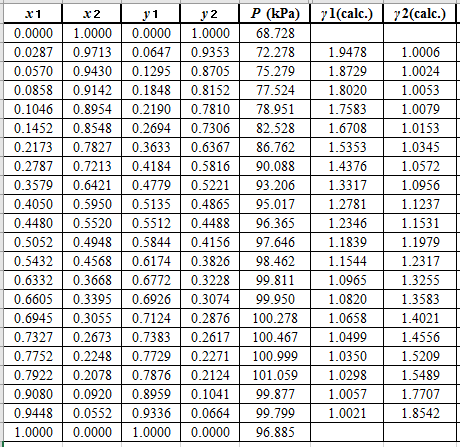
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

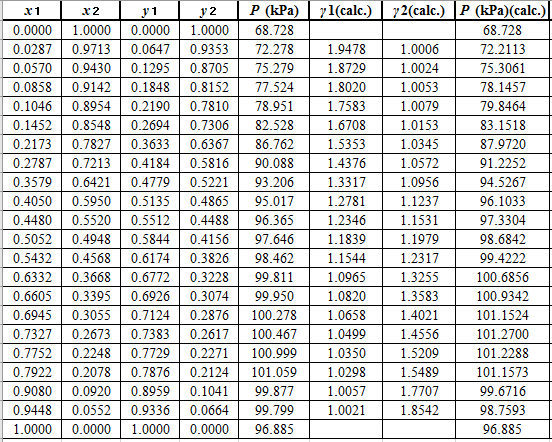
Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=0.8522\end{array}$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

(b)

Interpretation Introduction

Interpretation:

The parameter values for the van Laar equation which provide the best fit of $G^E/RT$to the given data are to be determined. Also, a $P-x-y$diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

The formula to calculate the value of $G^E/RT$for a binary system is:

  $\frac{G^E}{RT}=x_1\ln {\gamma }_1+x_2\ln {\gamma }_2$   ...... (2)

Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=x_1{x}_2\frac{A_{12}{A}_{21}}{\left(A_{12}{x}_1+A_{21}{x}_2\right)}$   ...... (6)

Here, $A_{12}\text{ and }{A}_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$from van Laar equation are:

  $\begin{array}{c}\ln {\gamma }_1=A_{12}{\left(1+\frac{A_{12}{x}_1}{A_{21}{x}_2}\right)}^{-2}\\ \ln {\gamma }_2=A_{21}{\left(1+\frac{A_{21}{x}_2}{A_{12}{x}_1}\right)}^{-2}\end{array}$   ...... (7)

Answer to Problem 13.34P

The parameter values for the van Laar equation which provide the best fit of $G^E/RT$to the given data are:

  $\begin{array}{c}{A}_{12}=0.693\\ A_{21}=0.686\end{array}$

The $P-x-y$diagram for the binary system containing methanol(1)/water(2) at ${\text{55}}^{\circ }\text{C}$for both calculated as well as experimental values are shown below. The values do not deviate by considerable extent from each other.

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol (1)/water (2) at ${\text{55}}^{\circ }\text{C}$is:

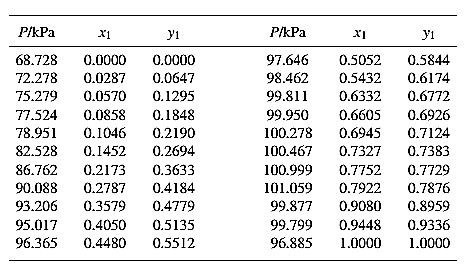
From the given data, first calculate the value of $x_2,\text{ and }{y}_2$and tabulating them in excel spreadsheet as shown below:

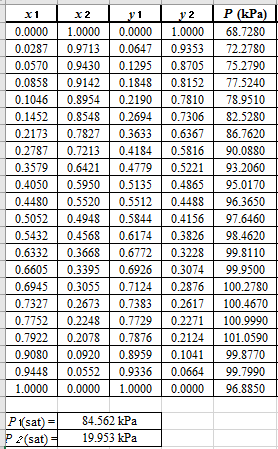
Now, use equation (1) for the Modifies Raoult’s law and calculate the value of ${\gamma }_1\text{ and }{\gamma }_2$using the below mentioned formula and tabulate it in the excel spreadsheet.

  $\begin{array}{c}{\gamma }_1=\frac{y_{1}P}{x_1{P}_1{}^{\text{sat}}}\\ {\gamma }_2=\frac{y_{2}P}{x_2{P}_2{}^{\text{sat}}}\end{array}$

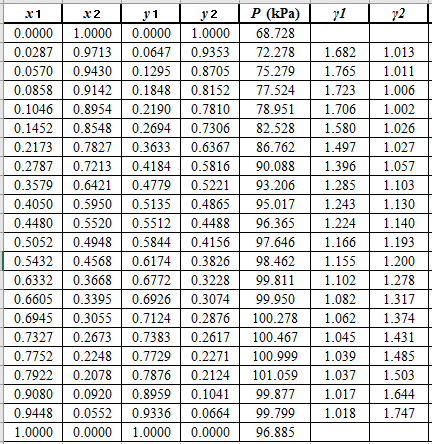
Use the equation (2) to calculate the value of $G^E/RT$for every value of $x_1$and tabulate it in the excel spreadsheet as shown below:

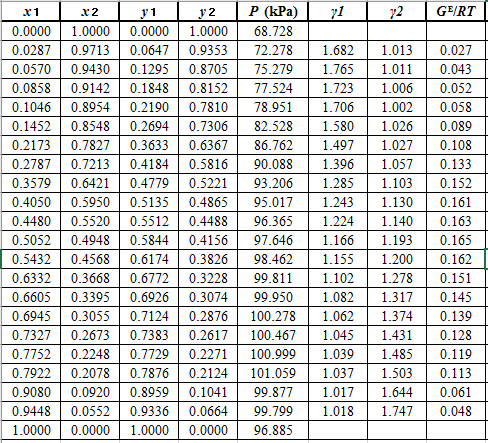
Rewrite equation (6) so that the equation becomes linear in $x_1$as:

  $\begin{array}{c}\left(\frac{G^E/RT}{x_1{x}_2}\right)=\frac{A_{12}{A}_{21}}{\left(A_{12}{x}_1+A_{21}{x}_2\right)}\\ \left(\frac{x_1{x}_2}{G^E/RT}\right)=\frac{\left(A_{12}{x}_1+A_{21}{x}_2\right)}{A_{12}{A}_{21}}=\frac{A_{12}{x}_1}{A_{12}{A}_{21}}+\frac{A_{21}{x}_2}{A_{12}{A}_{21}}\\ \left(\frac{x_1{x}_2}{G^E/RT}\right)=\frac{x_1}{A_{21}}+\frac{1-x_1}{A_{12}}\\ \left(\frac{x_1{x}_2}{G^E/RT}\right)=\left(\frac{1}{A_{21}}-\frac{1}{A_{12}}\right)x_1+\frac{1}{A_{12}}\mathrm{......}\text{ (8)}\end{array}$

Now, calculate the values of $\left(\frac{x_1{x}_2}{G^E/RT}\right)$as shown below:

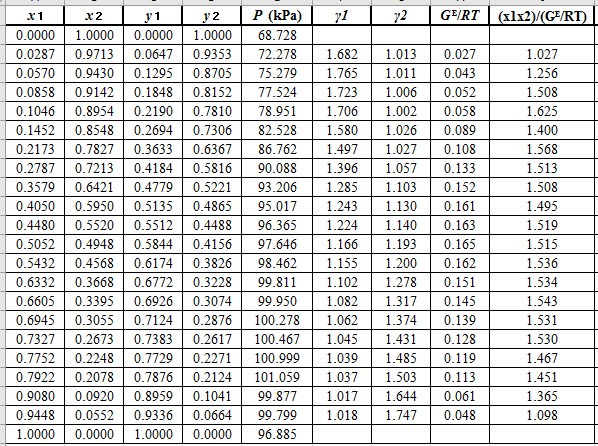
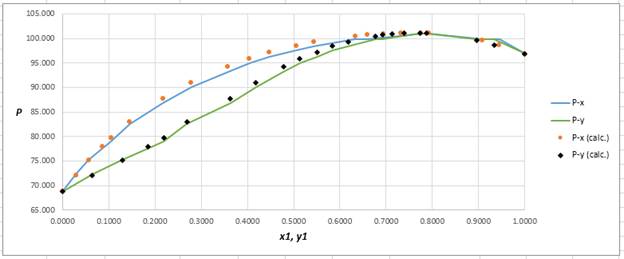
Plot the graph of $\left(\frac{x_1{x}_2}{G^E/RT}\right)$versus $x_1$and using the excel toolas:

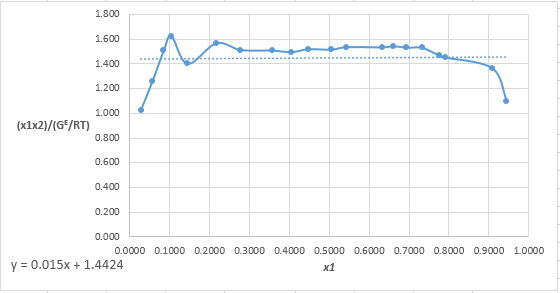
The equation that fits the plot is:

  $\left(\frac{x_1{x}_2}{G^E/RT}\right)=0.015x_1+1.4424$

Compare it with equation (8) so that the values of $A_{12}\text{ and }{A}_{21}$will be:

  $\begin{array}{c}\text{intercept}=1.4424=\frac{1}{A_{12}}\\ A_{12}=\frac{1}{1.4424}=0.693\\ \text{slope}=0.015=\frac{1}{A_{21}}-\frac{1}{A_{12}}\\ 0.015=\frac{1}{A_{21}}-\frac{1}{0.693}\\ A_{21}=\frac{1}{0.015+\frac{1}{0.693}}=0.686\end{array}$

According to the above correlation for $G^E/RT$and the values of $A_{12}\text{ and }{A}_{21}$, the correlations for $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$using the equation set (7) will be:

  $\begin{array}{c}\ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=A_{12}{\left(1+\frac{A_{12}{x}_1}{A_{21}{x}_2}\right)}^{-2}\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left[0.693{\left(1+\frac{0.693x_1}{0.686x_2}\right)}^{-2}\right]\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left[0.693{\left(1+1.0102\frac{x_1}{x_2}\right)}^{-2}\right]\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=A_{21}{\left(1+\frac{A_{21}{x}_2}{A_{12}{x}_1}\right)}^{-2}\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left[0.686{\left(1+\frac{0.686x_2}{0.693x_1}\right)}^{-2}\right]\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left[0.686{\left(1+0.9899\frac{x_2}{x_1}\right)}^{-2}\right]\end{array}$

Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

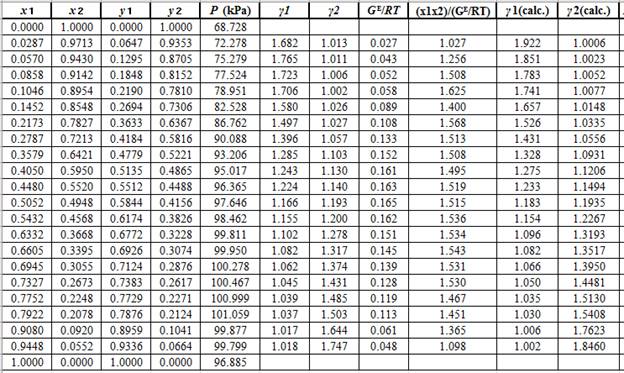
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

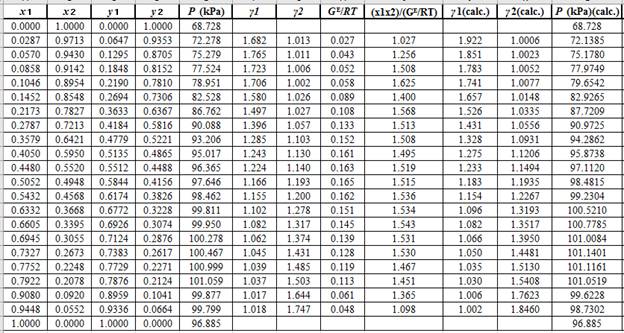
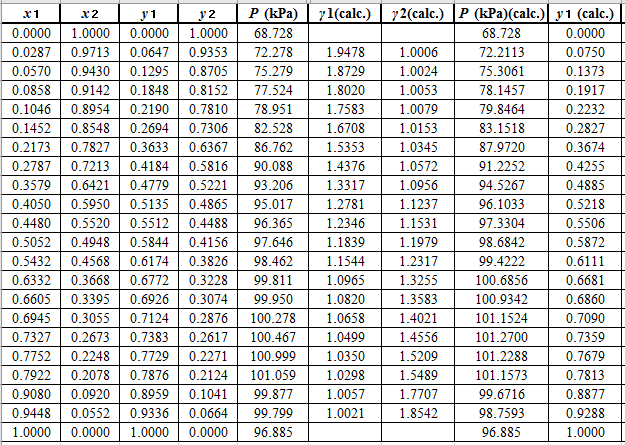
Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

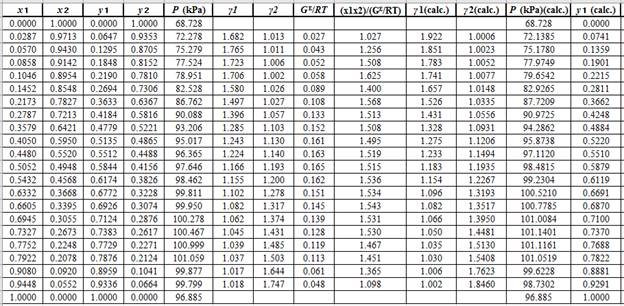
Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

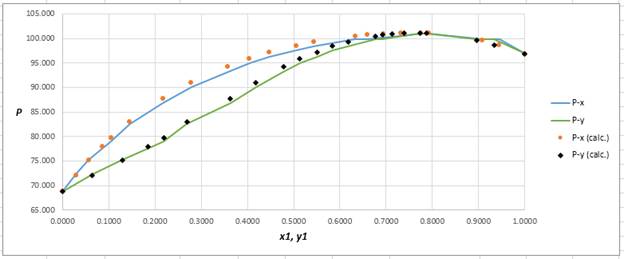
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=0.698\end{array}$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

(c)

Interpretation Introduction

Interpretation:

The parameter values for the Wilson equation which provide the best fit of $G^E/RT$to the given data are to be determined. Also, a $P-x-y$diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

The formula to calculate the value of $G^E/RT$for a binary system is:

  $\frac{G^E}{RT}=x_1\ln {\gamma }_1+x_2\ln {\gamma }_2$   ...... (2)

Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=-x_1\ln \left(x_1+x_2{\Lambda }_{12}\right)-x_2\ln \left(x_2-x_1{\Lambda }_{21}\right)$   ...... (9)

Here, ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$from Wilson equation are:

  $\begin{array}{c}\ln {\gamma }_1=-\ln \left(x_1+x_2{\Lambda }_{12}\right)+x_2\left(\frac{{\Lambda }_{12}}{x_1+x_2{\Lambda }_{12}}-\frac{{\Lambda }_{21}}{x_2+x_1{\Lambda }_{21}}\right)\\ \ln {\gamma }_2=-\ln \left(x_2+x_1{\Lambda }_{21}\right)+x_1\left(\frac{{\Lambda }_{12}}{x_1+x_2{\Lambda }_{12}}-\frac{{\Lambda }_{21}}{x_2+x_1{\Lambda }_{21}}\right)\end{array}$   ...... (10)

Answer to Problem 13.34P

The parameter values for the Wilson equation which provide the best fit of $G^E/RT$to the given data are:

  $\begin{array}{c}{\Lambda }_{12}=0.710\\ {\Lambda }_{21}=0.681\end{array}$

The $P-x-y$diagram for the binary system containing methanol(1)/water(2) at ${\text{55}}^{\circ }\text{C}$for both calculated as well as experimental values are shown below. The values deviate by considerable extent from each other.

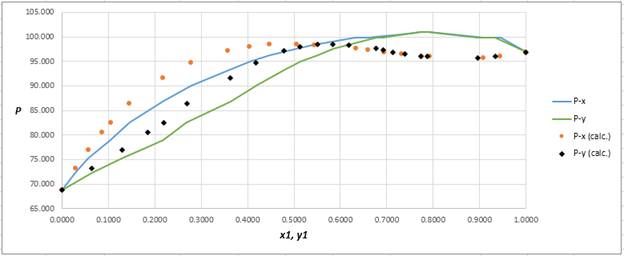
Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at ${\text{55}}^{\circ }\text{C}$is:

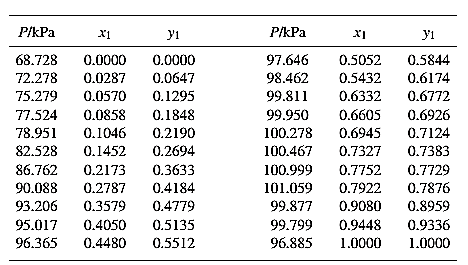
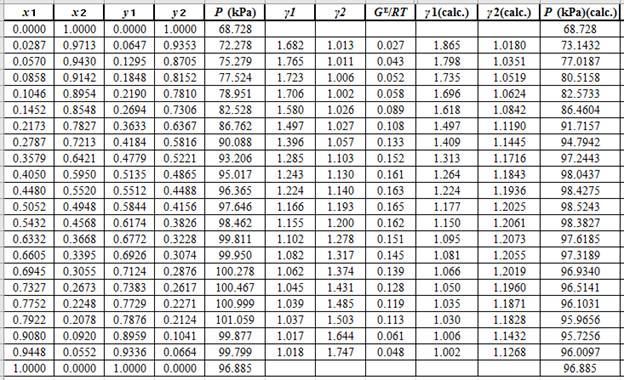
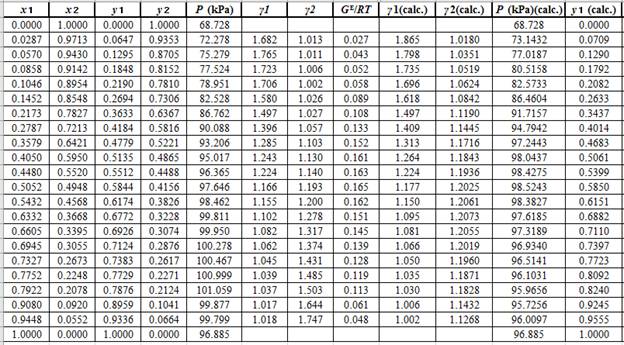
From the given data, first calculate the value of $x_2,\text{ and }{y}_2$and tabulating them in excel spreadsheet as shown below:

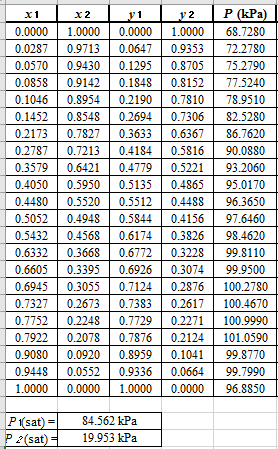
Now, use equation (1) for the Modifies Raoult’s law and calculate the value of ${\gamma }_1\text{ and }{\gamma }_2$using the below mentioned formula and tabulate it in the excel spreadsheet.

  $\begin{array}{c}{\gamma }_1=\frac{y_{1}P}{x_1{P}_1{}^{\text{sat}}}\\ {\gamma }_2=\frac{y_{2}P}{x_2{P}_2{}^{\text{sat}}}\end{array}$

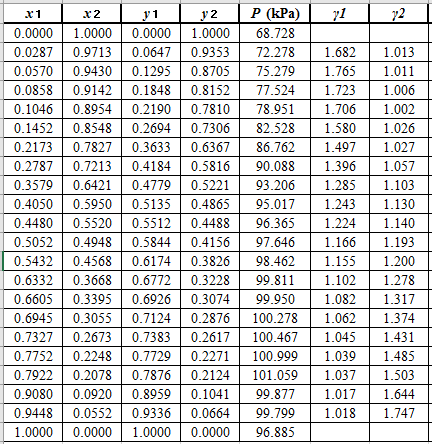
Use the equation (2) to calculate the value of $G^E/RT$for every value of $x_1$and tabulate it in the excel spreadsheet as shown below:

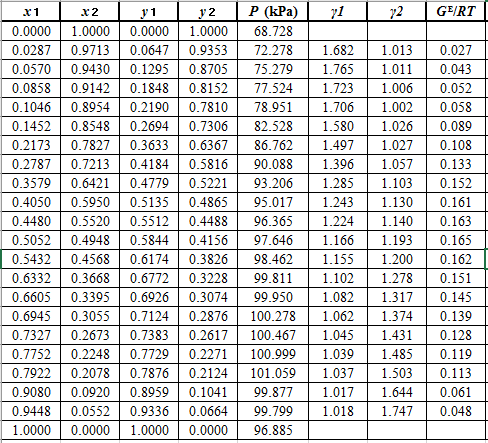
Now, use the method of the non-linear least square and fit the $G^E/RT$data into equation (9). First guess a value for ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$as $0.5\text{ and 1}\text{.0}$respectively, then use it to calculate $G^E/RT$for each value of $x_1$ . Then find the sum of the squared errors and minimize this value to get the value of the parameters ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$as:

  $\begin{array}{c}{\Lambda }_{12}=0.710\\ {\Lambda }_{21}=0.681\end{array}$

Use the values of ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$and the correlations in equation set (10) to calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$ as:

Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

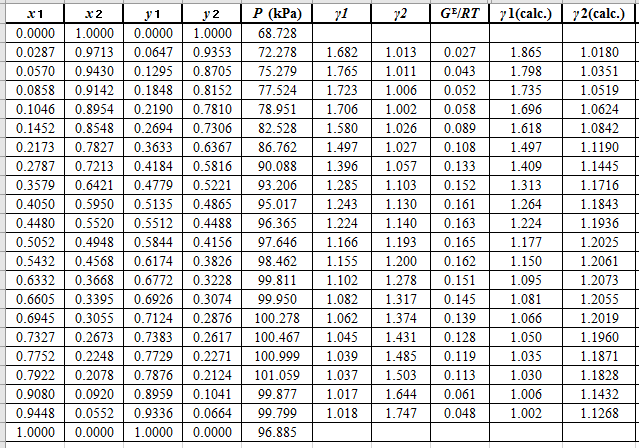
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

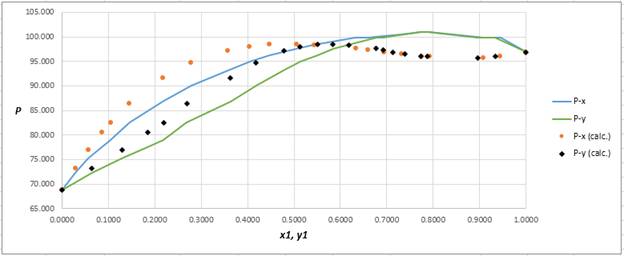
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=3.45\end{array}$

Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.

(d)

Interpretation Introduction

Interpretation:

The parameter values for the Margules equation which provide the best fit of $P-x_1$data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $\delta P\text{ and }\delta y_1$which are plotted versus $x_1$ .

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=\left(A_{12}{x}_1+A_{21}{x}_2\right)x_1{x}_2$   ...... (3)

Here, $A_{12}\text{ and }{A}_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$are:

  $\begin{array}{c}\ln {\gamma }_1=x_2^2\left[A_{12}+2\left(A_{21}-A_{12}\right)x_1\right]\\ \ln {\gamma }_2=x_1^2\left[A_{21}+2\left(A_{12}-A_{21}\right)x_2\right]\end{array}$   ...... (4)

Answer to Problem 13.34P

The parameter values for the Margules equation which provide the best fit of $P-x_1$data using Barker’s method data are:

  $\begin{array}{c}{A}_{12}=0.644\\ A_{21}=0.672\end{array}$

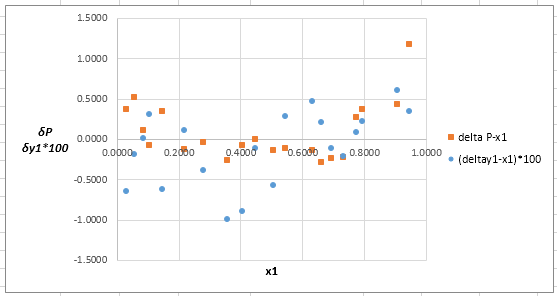
The plot residuals $\delta P\text{ and }\delta y_1$versus $x_1$on same graph is:

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at ${\text{55}}^{\circ }\text{C}$is:

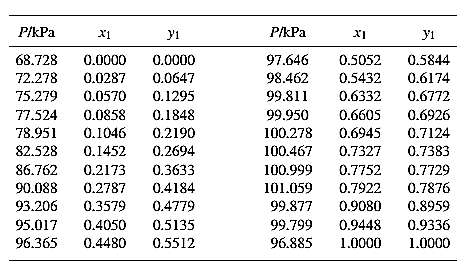
Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A_{12}\text{ and }{A}_{21}$as $0.5\text{ and 1}\text{.0}$respectively, then use it to determine the value of ${\gamma }_1\text{ and }{\gamma }_2$using equation (4) for each value of $x_1$ .

Now, calculate the value of ${\left(P\right)}_{\text{calc}\text{.}}$for each value of $x_1$using equation (1) and ${\gamma }_1\text{ and }{\gamma }_2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters $A_{12}\text{ and }{A}_{21}$as:

  $\begin{array}{c}\text{SSE}={\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}\\ \left(\text{Here, }n\text{ is the number of entries}\right)\\ A_{12}=0.644\\ A_{21}=0.672\end{array}$

Using the equation set (4) and the parameter values, deduce the relation for ${\gamma }_1\text{ and }{\gamma }_2$ as:

  $\begin{array}{c}\ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=x_2^2\left[A_{12}+2\left(A_{21}-A_{12}\right)x_1\right]\\ \ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=x_2^2\left[0.644+2\left(0.672-0.644\right)x_1\right]\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left(x_2^2\left[0.644+0.056x_1\right]\right)\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=x_1^2\left[A_{21}+2\left(A_{12}-A_{21}\right)x_2\right]\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=x_1^2\left[0.672+2\left(0.644-0.672\right)x_2\right]\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left(x_1^2\left[0.672-0.056x_2\right]\right)\end{array}$

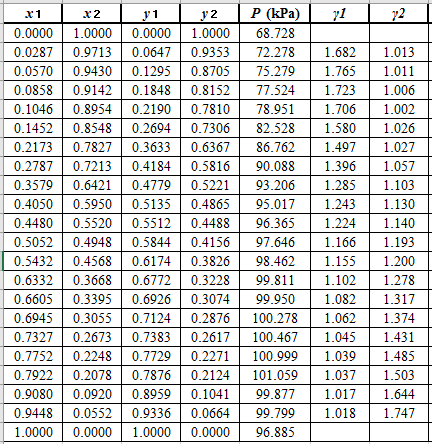
Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

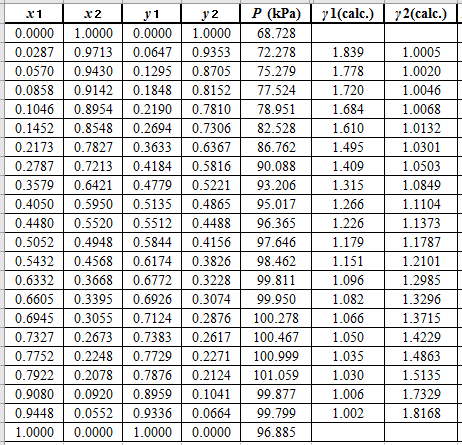
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

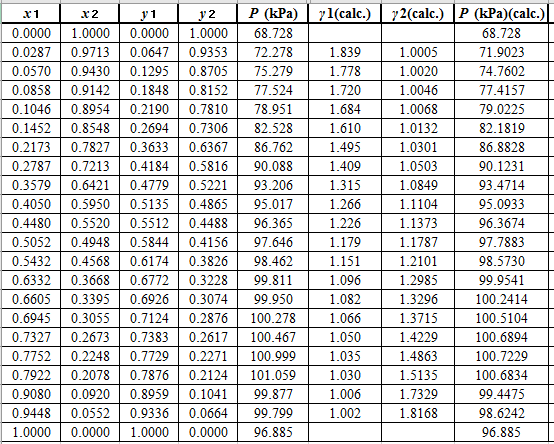
Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

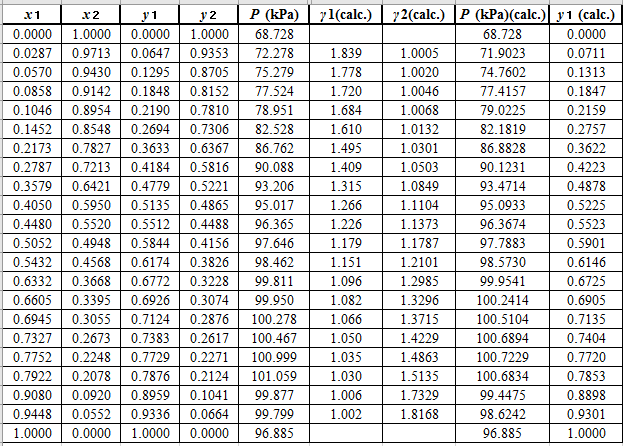
Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

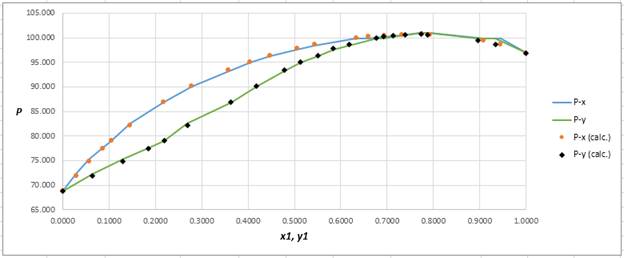
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=0.365\end{array}$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

Now, calculate the residuals $\delta P\text{ and }\delta y_1$as shown. Also, calculate $\delta y_1\times 100$as $\delta y_1$is very small and is difficult to plot on same graph as $\delta P$ .

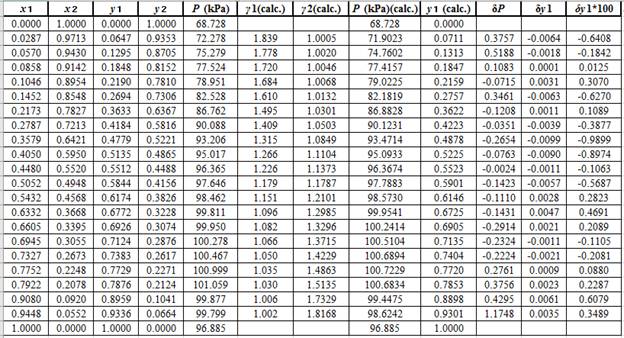
Plot these residuals against $x_1$on same graph as:

(e)

Interpretation Introduction

Interpretation:

The parameter values for the van Laar equation which provide the best fit of $P-x_1$data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $\delta P\text{ and }\delta y_1$which are plotted versus $x_1$ .

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=x_1{x}_2\frac{A_{12}{A}_{21}}{\left(A_{12}{x}_1+A_{21}{x}_2\right)}$   ...... (6)

Here, $A_{12}\text{ and }{A}_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$from van Laar equation are:

  $\begin{array}{c}\ln {\gamma }_1=A_{12}{\left(1+\frac{A_{12}{x}_1}{A_{21}{x}_2}\right)}^{-2}\\ \ln {\gamma }_2=A_{21}{\left(1+\frac{A_{21}{x}_2}{A_{12}{x}_1}\right)}^{-2}\end{array}$   ...... (7)

Answer to Problem 13.34P

The parameter values for the van Laar equation which provide the best fit of $P-x_1$data using Barker’s method data are:

  $\begin{array}{c}{A}_{12}=0.644\\ A_{21}=0.672\end{array}$

The plot residuals $\delta P\text{ and }\delta y_1$versus $x_1$on same graph is:

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol (1)/ water (2) at ${\text{55}}^{\circ }\text{C}$is:

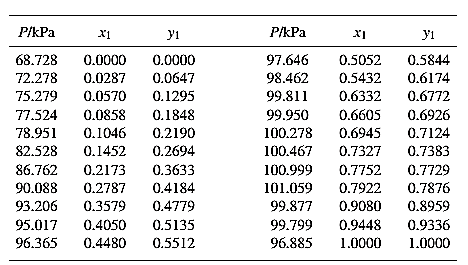
Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A_{12}\text{ and }{A}_{21}$as $0.5\text{ and 1}\text{.0}$respectively, then use it to determine the value of ${\gamma }_1\text{ and }{\gamma }_2$using equation (7) for each value of $x_1$ .

Now, calculate the value of ${\left(P\right)}_{\text{calc}\text{.}}$for each value of $x_1$using equation (1) and ${\gamma }_1\text{ and }{\gamma }_2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters $A_{12}\text{ and }{A}_{21}$as:

  $\begin{array}{c}\text{SSE}={\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}\\ \left(\text{Here, }n\text{ is the number of entries}\right)\\ A_{12}=0.644\\ A_{21}=0.672\end{array}$

Using the equation set (7) and the parameter values, deduce the relation for ${\gamma }_1\text{ and }{\gamma }_2$ as:

  $\begin{array}{c}\ln {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=A_{12}{\left(1+\frac{A_{12}{x}_1}{A_{21}{x}_2}\right)}^{-2}\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left[0.644{\left(1+\frac{0.644x_1}{0.672x_2}\right)}^{-2}\right]\\ {\left({\gamma }_1\right)}_{\text{calc}\text{.}}=\exp \left[0.644{\left(1+0.958\frac{x_1}{x_2}\right)}^{-2}\right]\\ \ln {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=A_{21}{\left(1+\frac{A_{21}{x}_2}{A_{12}{x}_1}\right)}^{-2}\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left[0.672{\left(1+\frac{0.672x_2}{0.644x_1}\right)}^{-2}\right]\\ {\left({\gamma }_2\right)}_{\text{calc}\text{.}}=\exp \left[0.672{\left(1+1.043\frac{x_2}{x_1}\right)}^{-2}\right]\end{array}$

Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

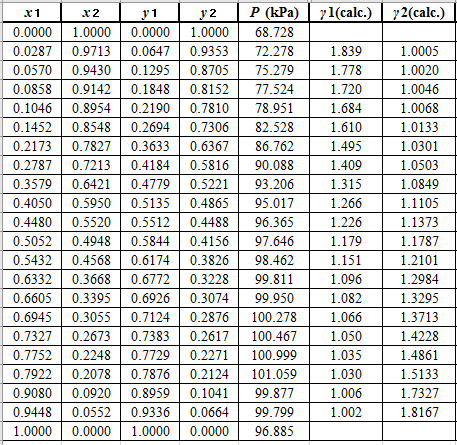
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

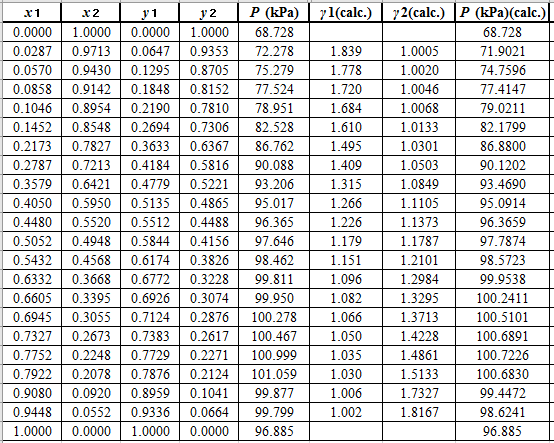
Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

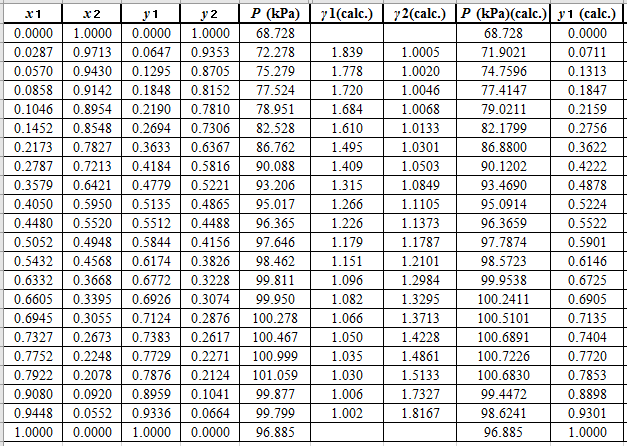
Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

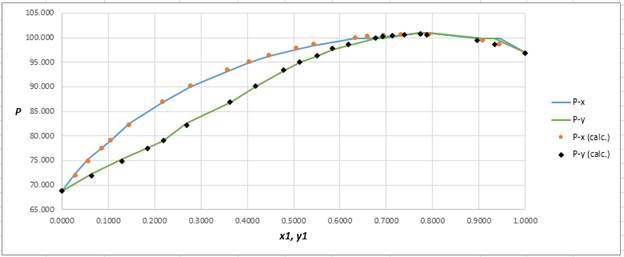
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=0.364\end{array}$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

Now, calculate the residuals $\delta P\text{ and }\delta y_1$as shown. Also, calculate $\delta y_1\times 100$as $\delta y_1$is very small and is difficult to plot on same graph as $\delta P$ .

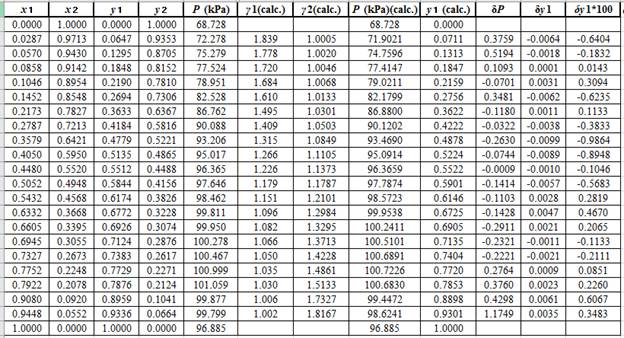
Plot these residuals against $x_1$on same graph as:

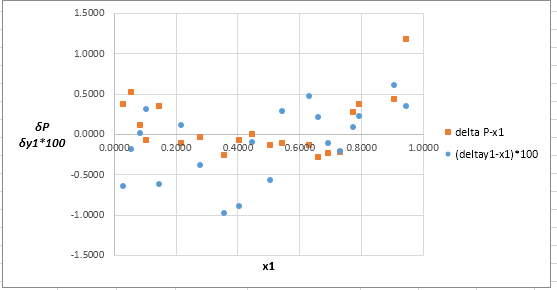
(f)

Interpretation Introduction

Interpretation:

The parameter values for the Wilson equation which provide the best fit of $P-x_1$data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $\delta P\text{ and }\delta y_1$which are plotted versus $x_1$ .

Concept Introduction:

Equation $13.19$to be used for Modified Raoult’s law is:

  $y_{i}P=x_i{\gamma }_i{P}_i{}^{\text{sat}}$   ...... (1)

Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

  $\frac{G^E}{RT}=-x_1\ln \left(x_1+x_2{\Lambda }_{12}\right)-x_2\ln \left(x_2-x_1{\Lambda }_{21}\right)$   ...... (9)

Here, ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$are the temperature dependent parameters, specific for a system.

The equations used to calculate $\ln {\gamma }_1\text{ and }\ln {\gamma }_2$from Wilson equation are:

  $\begin{array}{c}\ln {\gamma }_1=-\ln \left(x_1+x_2{\Lambda }_{12}\right)+x_2\left(\frac{{\Lambda }_{12}}{x_1+x_2{\Lambda }_{12}}-\frac{{\Lambda }_{21}}{x_2+x_1{\Lambda }_{21}}\right)\\ \ln {\gamma }_2=-\ln \left(x_2+x_1{\Lambda }_{21}\right)+x_1\left(\frac{{\Lambda }_{12}}{x_1+x_2{\Lambda }_{12}}-\frac{{\Lambda }_{21}}{x_2+x_1{\Lambda }_{21}}\right)\end{array}$   ...... (10)

Answer to Problem 13.34P

The parameter values for the Wilson equation which provide the best fit of $P-x_1$data using Barker’s method data are:

  $\begin{array}{c}{\Lambda }_{12}=0.732\\ {\Lambda }_{21}=0.663\end{array}$

The plot residuals $\delta P\text{ and }\delta y_1$versus $x_1$on same graph is:

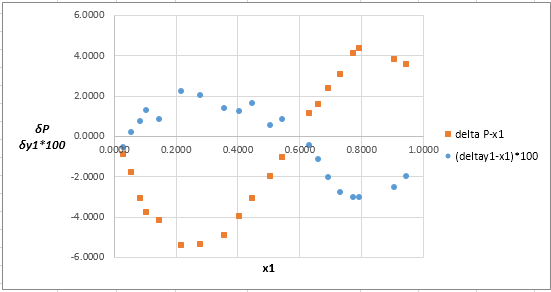
Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol (1)/water (2) at ${\text{55}}^{\circ }\text{C}$is:

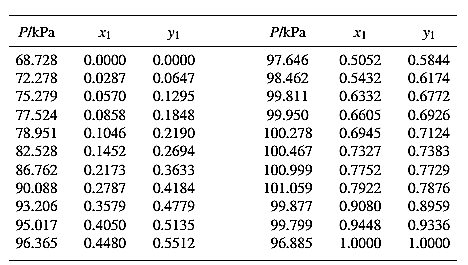
Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A_{12}\text{ and }{A}_{21}$as $0.5\text{ and 1}\text{.0}$respectively, then use it to determine the value of ${\gamma }_1\text{ and }{\gamma }_2$using equation (10) for each value of $x_1$ .

Now, calculate the value of ${\left(P\right)}_{\text{calc}\text{.}}$for each value of $x_1$using equation (1) and ${\gamma }_1\text{ and }{\gamma }_2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters ${\Lambda }_{12}\text{ and }{\Lambda }_{21}$as:

  $\begin{array}{c}\text{SSE}={\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}\\ \left(\text{Here, }n\text{ is the number of entries}\right)\\ {\Lambda }_{12}=0.732\\ {\Lambda }_{21}=0.663\end{array}$

Using the equation set (10) and the parameter values, deduce the relation for ${\gamma }_1\text{ and }{\gamma }_2$ as:

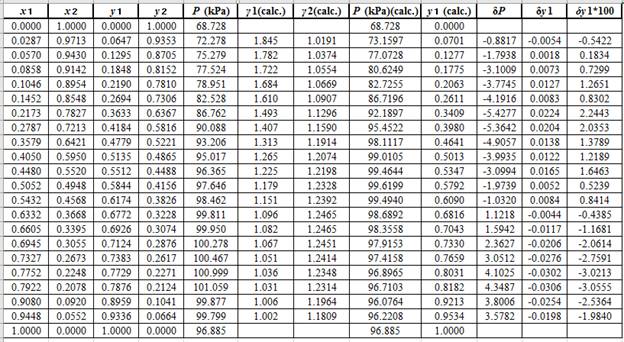
Now, using the above relations, calculate the values of ${\gamma }_1\text{ and }{\gamma }_2$for each value of $x_1\text{ and }{x}_2$and tabulate the data in the excel spreadsheet as:

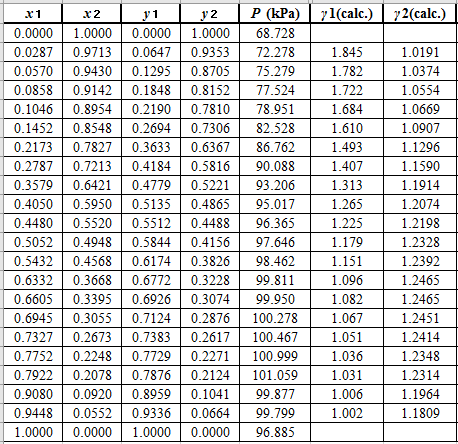
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x_1\text{ and }{x}_2$using the calculated values of ${\gamma }_1\text{ and }{\gamma }_2$as:

  ${\left(P\right)}_{\text{calc}\text{.}}=x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}+x_2{\left({\gamma }_2\right)}_{\text{calc}\text{.}}{P}_2{}^{\text{sat}}$

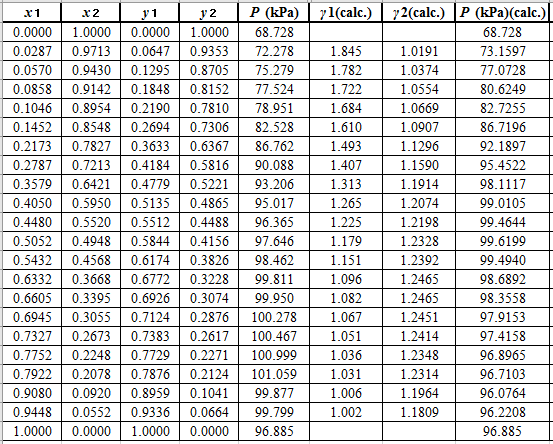
Now, use the below mentioned formula to calculate the value of $y_1$for each of the calculated value of $P$as:

  ${\left(y_1\right)}_{\text{calc}\text{.}}=\frac{x_1{\left({\gamma }_1\right)}_{\text{calc}\text{.}}{P}_1{}^{\text{sat}}}{{\left(P\right)}_{\text{calc}\text{.}}}$

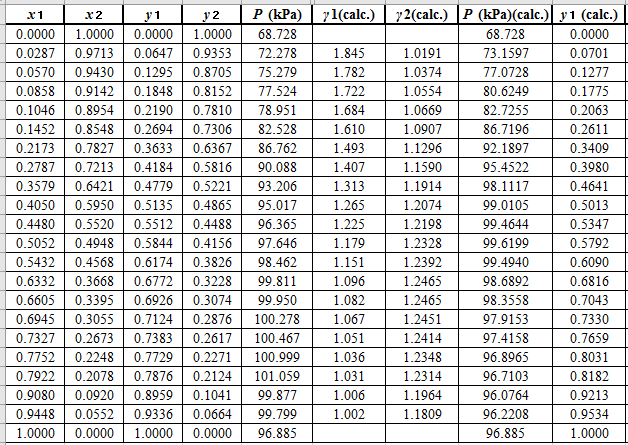
Using the tools of the excel, plot the graph of ${\left(P-x\right)}_{\text{calc}\text{.}}\text{, }{\left(P-y\right)}_{\text{calc}\text{.}},P-x,\text{ and }P-y$and mark labels as shown below:

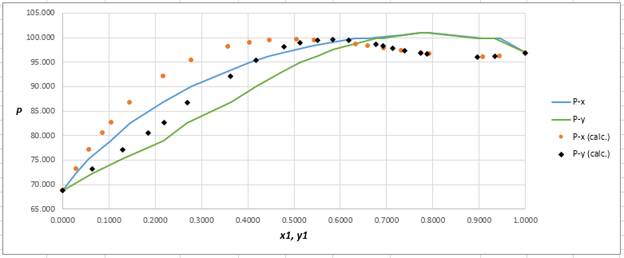
Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

  $\begin{array}{c}\text{RMS}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{\left(P_i-{\left(P_i\right)}_{\text{calc}\text{.}}\right)}^2}}{n}}\\ \text{Here, }n\text{ is number of entries}\text{.}\\ \text{RMS}=3.464\end{array}$

Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.

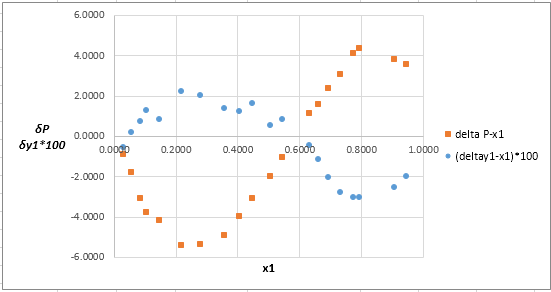
Now, calculate the residuals $\delta P\text{ and }\delta y_1$as shown. Also, calculate $\delta y_1\times 100$as $\delta y_1$is very small and is difficult to plot on same graph as $\delta P$ .

Plot these residuals against $x_1$on same graph as: