
(a)
Interpretation:
Assuming Raoult’s law is valid we need to find the values of liquid mole fraction of n-pentane(1) and vapor mole fraction of n-pentane(1) for a binary system of n-pentane(1) and n-heptane(2) for temperature 65°C and when total pressure
Assuming Raoult’s law is valid we need to plot the total pressure P, liquid mole fraction of n-pentane (1), x1, vapor fraction of n-pentane (1), y1 vs. fraction of system that is vapor V for the binary system of n-pentane(1) and n-heptane(2) at these same conditions at temperature
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(a)
Answer to Problem 13.4P
V is linear in z1

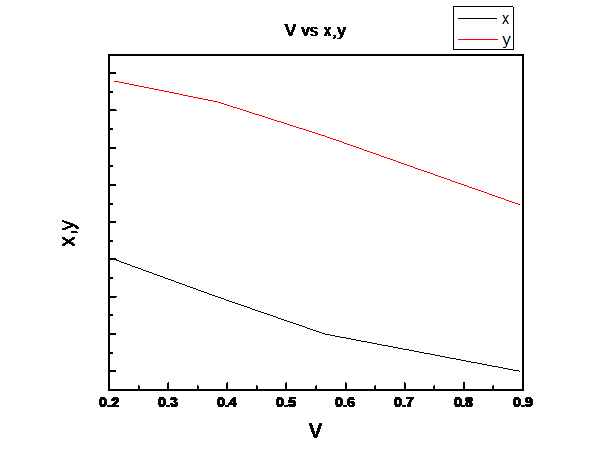

Explanation of Solution
Find the value of
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
Therefore, total pressure,
By equating total pressure
Using the formula
we find 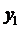
For the given temperature, z1 ranges from the liquid composition at the bubble point to the vapor composition at the dew point.
Now,
So, V is linear in z1

Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
So, the expression for total pressure
Using the formula
we find 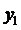
Now,
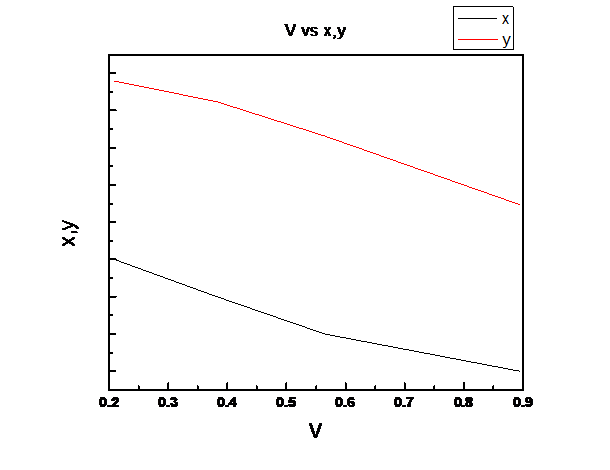

(b)
Interpretation:
Assuming Raoult’s law is valid we need to find the values of liquid mole fraction of n-pentane(1) and vapor mole fraction of n-pentane(1) for a binary system of n-pentane(1) and n-heptane(2) for temperature 75°C and when total pressure
Assuming Raoult’s law is valid we need to plot the total pressure P, liquid mole fraction of n-pentane (1), x1, vapor fraction of n-pentane (1), y1 vs. fraction of system that is vapor V for the binary system of n-pentane(1) and n-heptane(2) at these same conditions at temperature
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(b)
Answer to Problem 13.4P
V is linear in z1


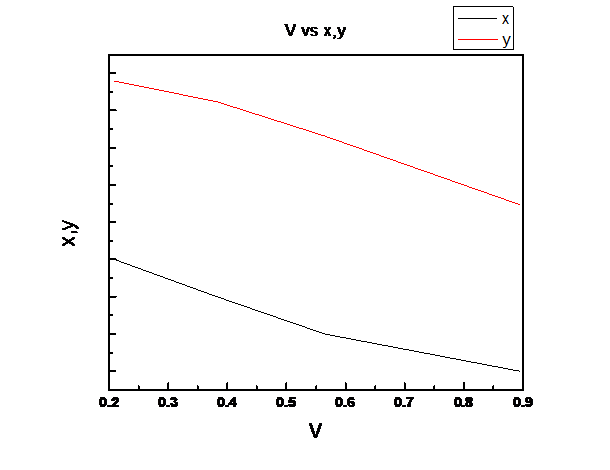

Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Find the value of
Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
Therefore, total pressure,
By equating total pressure
Using the formula
we find 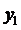
For the given temperature, z1 ranges from the liquid composition at the bubble point to the vapor composition at the dew point.
Now,
So, V is linear in z1


Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
So, the expression for total pressure
Using the formula
we find 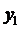
Now,
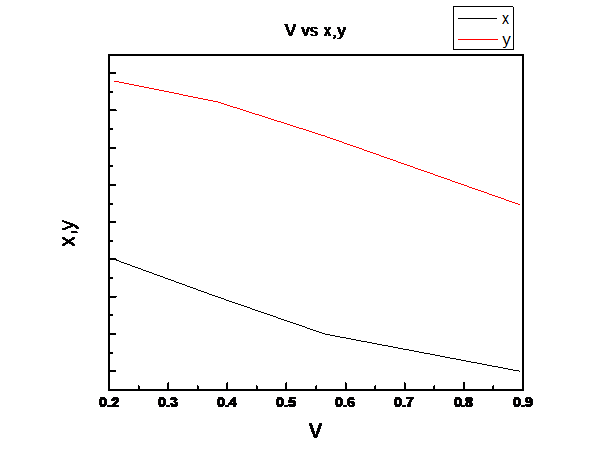

(c)
Interpretation:
Assuming Raoult’s law is valid we need to find the values of liquid mole fraction of n-pentane(1) and vapor mole fraction of n-pentane(1) for a binary system of n-pentane(1) and n-heptane(2) for temperature 85°C and when total pressure
Assuming Raoult’s law is valid we need to plot the total pressure P, liquid mole fraction of n-pentane (1), x1, vapor fraction of n-pentane (1), y1 vs. fraction of system that is vapor V for the binary system of n-pentane(1) and n-heptane(2) at these same conditions at temperature
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(c)
Answer to Problem 13.4P
V is linear in z1


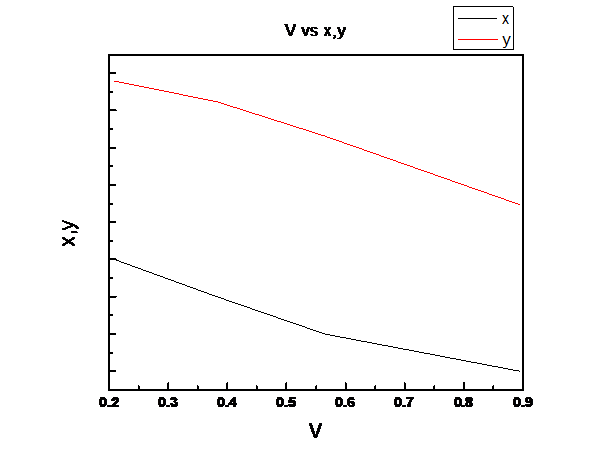

Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Find the value of
Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
Therefore, total pressure,
By equating total pressure
Using the formula
we find 
For the given temperature, z1 ranges from the liquid composition at the bubble point to the vapor composition at the dew point.
Now,
So, V is linear in z1

Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
So, the expression for total pressure
Using the formula
we find 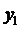
Now,

(d)
Interpretation:
Assuming Raoult’s law is valid we need to find the values of liquid mole fraction of n-pentane(1) and vapor mole fraction of n-pentane(1) for a binary system of n-pentane(1) and n-heptane(2) for temperature 95°C and when total pressure
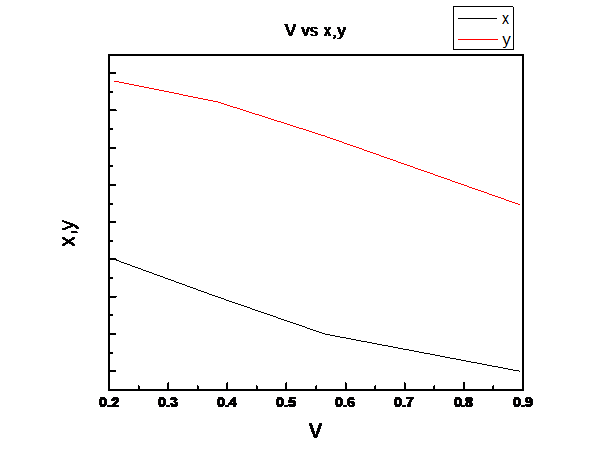
Assuming Raoult’s law is valid we need to plot the total pressure P, liquid mole fraction of n-pentane (1), x1, vapor fraction of n-pentane (1), y1 vs. fraction of system that is vapor V for the binary system of n-pentane(1) and n-heptane(2) at these same conditions at temperature
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(d)
Answer to Problem 13.4P
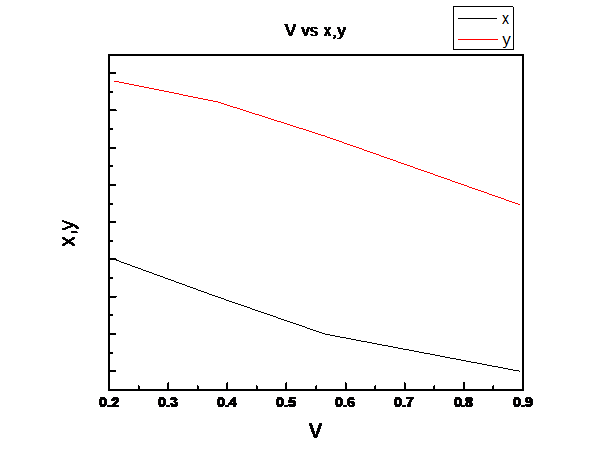
V is linear in z1


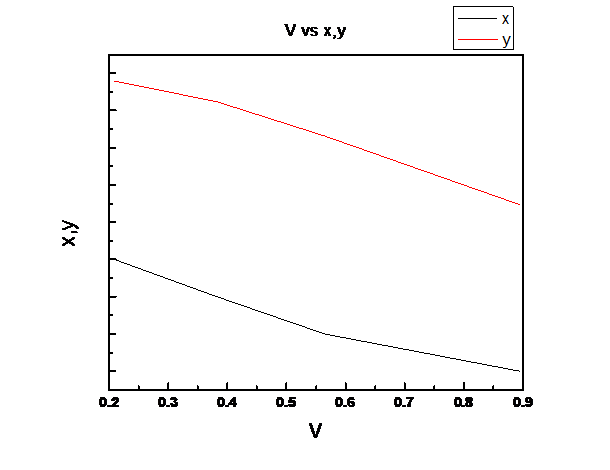

Explanation of Solution
Find the value of
Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
Therefore, total pressure,
By equating total pressure
Using the formula
we find 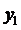
For the given temperature, z1 ranges from the liquid composition at the bubble point to the vapor composition at the dew point.
Now,
So, V is linear in z1
 Now, For n-pentane (1)
Now, For n-pentane (1)
And For n-heptane (2)
Now vapor pressure for n-pentane (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for n-heptane (2) can be calculated using Antoine equation as follows:
So, the expression for total pressure
Using the formula
we find 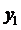
Now,

Want to see more full solutions like this?
Chapter 13 Solutions
Loose Leaf For Introduction To Chemical Engineering Thermodynamics
- A distillation column with 100 kmol/h feed of 50% A and 50% B produces a distillate product with xD = 0.95 and a bottom stream with xbot = 0.04 of the more volatile species A. CMO is valid and the equilibrium data is given by y = 2.4x/1 + 1.4x a) If the feed is saturated liquid, determine the minimum reflux ratio b) If the feed is saturated vapor, determine the minimum reflux ratioarrow_forwardA distillation column with 100 kmol/h feed of 60% A and 40% B produces a distillate product with xD = 0.98 and a bottom stream with xbot = 0.02 of the more volatile species A. CMO is valid and the equilibrium data is given by y = 2.2x/1+1.2x a) If the reflux ratio R is 2, determine (numerically) the composition (y) of the vapor stream entering the top equilibrium plate.__________b) If R = 2 and q = 0.6, determine the liquid flow rate in the stripping section of the column__________c) If q = 0, the minimum reflux ratio isarrow_forwardNatural gas having a specific gravity relative to air of 0.60 and a viscosity of 0.011 cP is flowing through a 6-in. Schedule 40 pipe in which is installed a standard sharp-edged orifice equipped with flange taps. The gas is at 100°F and 20lb/in? abs at the upstream tap. The manometer reading is 46.3 in. of water at 60°F. The ratio of specific heats for natural gas is 1.30. The diameter of the orifice is 2.00 in. Calculate the rate of flow of gas through the line in cubic feet.arrow_forward
- صورة من s94850121arrow_forward11:01 ☑ canvas.ucsd.edu 口 : ... Page 1 > of 2 Q - ZOOM + 4. Consider the two separate sets of measured data for a silt-loam soil measured by Mualem (1976): (1) suction versus water content, and (2) suction versus relative permeability of unsaturated soil, k/ks. Assume that 0s 0.396, 0res = 0.131, and Ks=5.74×10-7 m/s. a. Using the method of least squares in Excel, compute the best-fit values for αNG (kPa¹) and nvg for the van Genuchten (1980) relationship for data set # 1 (assume m = 1-1/nvG). See the example spreadsheet in the homework folder under the files section of Canvas for help in performing this calculation. b. Repeat part (a) and estimate the λ and ac parameters for the Brooks and Corey (1964) SWRC for data set #1. Note that you may need to include an "if" statement at the air entry suction. c. Plot the data for the SWRC versus the fitted van Genuchten (1980) and Brooks and Corey (1964) curves. Which relationship matches the capillary pressure data better (BC or VG)? Explain…arrow_forwardSolve h.w 6arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





