
(a)
Interpretation:
The mole fraction of benzene in vapour phase, y1and constant total pressure, P at temperature 100°C is to be calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(a)
Answer to Problem 13.1P
(a)
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:
Using formula
Using the formula
we find mole fraction of benzene (1) in vapor phase, 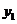
Therefore,
(b)
Interpretation:
The mole fraction of benzene in liquid phase, x1and constant total pressure, P at temperature 100°C is to be calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(b)
Answer to Problem 13.1P
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:
Using the formula
we find mole fraction of benzene (1) in liquid phase, 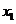
Using formula
Therefore,
(c)
Interpretation:
The mole fraction of benzene in vapor phase, y1and temperature of the solution, T at total pressure P =120 kPa is to be calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(c)
Answer to Problem 13.1P
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now,
Using formula
Solving this equation, we find
Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:
Using the formula
we find mole fraction of benzene (1) in vapor phase, 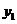
Therefore,
(d)
Interpretation:
The mole fraction of benzene in liquid phase, x1and temperature of the solution, T at total pressure P =120 kPa is to be calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(d)
Answer to Problem 13.1P
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now,
Solving these two equations, we find
Therefore,
(e)
Interpretation:
The mole fraction of benzene in liquid phase, x1and mole fraction of benzene in vapour phase, y1at total pressure P =120 kPa and temperature T=105 °C is to be calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(e)
Answer to Problem 13.1P
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now,
Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:
Using formula
Using the formula
Therefore,
(f)
Interpretation:
The overall mole fraction of benzene is z1=0.33 at total pressure P =120 kPa and temperature T=105 °C is given. The mole fraction of benzene and toluene in vapor phase needs to calculated.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(f)
Answer to Problem 13.1P
Vapor fraction, V is 0.231923 and liquid fraction is 0.768077
Explanation of Solution
The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-
and
The total pressure:
Where
The mole fraction of A in the vapor phase is given by -
Similarly, mole fraction of B in vapor phase is given by -
Now vapor pressures
Now, For benzene (1)
And For toluene (2)
Given
Now,
Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -
Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:
Using formula
Using the formula
Now,
Therefore, vapor fraction, V is 0.231923 and liquid fraction is 0.768077.
(g)
Interpretation:
To explain why Raoul’s law is likely to be an excellent VLE model for this system at the stated conditions.
Concept introduction:
Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-
Where
A solution behaves ideally when
- The solute and the solvent molecules have similar sizes and similar intermolecular forces,
- The excess volume of mixing is zero, and
- The heat of mixing is zero when both the solute and the solvent are liquids
(g)
Explanation of Solution
Benzene and toluene are both non-polar. They are similar in shape and size. Therefore, one would expect little chemical interaction between the two substances. Moreover, the temperature is sign enough and the pressure is low, so it is expected to behave ideally.
Want to see more full solutions like this?
Chapter 13 Solutions
EBK INTRODUCTION TO CHEMICAL ENGINEERIN
- 3. You are given a mixture of four proteins, whose properties are listed in the table below. Propose a process to purify each protein so that you end up with four solutions of pure protein. What resin would you use to bind the protein(s)? What changes to the buffer would you make to desorb the protein(s)? Contains an N-terminal His6-tag. Two 50 kDa subunits contain a non-heme Fe2+ in the active site. Protein Size (kDa) pl Specific Properties A 100 6.0 B 40 7.7 C 240 8.3 Ꭰ 225 5.5 Contains FAD redox center and an NADH binding domain. Composed of six 40-kDa subunits, each of which contains a [2Fe-2S] cluster. Composed of three subunits: 100 kDa structural subunit, 75 kDa subunit with a molybdopterin center, and 50 kDa subunit with FAD and an NADH binding domain.arrow_forwardb) Explain the key features of the Langmuir adsorption model - Drawing a diagram with empty and occupied sites. Show how new molecules would adsorb. drawing the diagram, showing free and empty sites, and their number (to use for next section) - Define the capacity and binding affinity parameters in terms of things shown on the diagram Defining the capacity and binding affinity parameters in terms of bound, free sites, and free molecules - Plot what would be a typical breakthrough curve and give an explanation approximately when breakthrough would occur plotting a typical sigmoidal breakthrough curve and saying it would certainly occur by the time capacity is used, but also could be much earlier if the affinity is lowarrow_forwardWater at 20°C flows at a steady average velocity of 5.25 m/s through a smooth pipe of diameter 5.08 cm. The flow is fully developed through the entire section of pipe. The total pipe length is 10.56 m, and there are two 90' elbows. Determine the friction coefficient and the head loss due to friction per meter length of the pipe. Control volume Prepared by Engr. Kirsten Gaarrow_forward
- Problem 2. For an irreversible liquid phase reaction A -> B, the reaction rate is of the first order with respect to the reactant concentration C_A. this reaction is performed in a cascade of two identical CSTRs at 100 degrees Celsius. (same reactor size and isothermal). The inlet concentration of A of the first CSTR is 2mol/L. The outlet concentration of A of the 2nd CSTR is 0.5 mol/L. the inlet flow rate of the 1st reactor is 100 L/h. and the feed temperature is 20 degrees Celsius. The average heat capacity of the reactant/product/solvent mixture is a constant: 2J/g*K, the density of the mixture is a constant: 1 kg/L. The heat of reaction is 50 kJ/mol (exothermic). The reaction rate constant at 100 degrees Celsius is 0.5/h. (a) Determine the outlet concentration of A of the first CSTR (b) What is the heat transfer requirement for the first CSTR? (c) if this reaction is performed in a plug-flow reactor, what is the size of plug-flow reactor required for achieving the same conversion…arrow_forwardThe energy release (Q_g) and energy loss (Q_r) curves of an irreversible oxidation reaction are shown below. Q_r curves can be shifted by adjusting the feed temperature. Q,& QE E Qg (a) Are these points of intersection between energy release and energy loss curves stable operating conditions? Point of Intersection A Stable or Unstable B A D T (b) Which point represents the ignition condition? B с D E F Garrow_forwardProblem 1. For an irreversible liquid phase reaction 2A -> B, the reaction rate is of the 2nd order with respect to the reactant concentration CA. The concentration-dependent reaction rate is plotted below. This reaction is performed in a cascade of two identical CSTRS (same reactor size and temperature). The inlet concentration of A of the 1st CSTR is 2 mol/L. The outlet concentration of A of the 2nd CSTR is 1 mol/L. The inlet flow rate of the 1st reactor is 100 L/h. Please use the graphical method to determine the outlet concentration of A of the first CSTR and the size of each CSTR. Please briefly show the procedure for reactor size calculation. (-4-7) 15225050 45 40 35 30 0 0.5 11.761.5 C₂ Q C (mol.L¹) Co 20 2.5arrow_forward
- 15.15 A 0.20-m-thick brick wall (k = 1.3 W/m K) separates the combustion zone of a furnace from its surroundings at 25°C. For an outside wall surface temperature of 100°C, with a convective heat-transfer coefficient of 18 W/m² K, what will be the inside wall surface temperature at steady-state conditions? .arrow_forwardAn MF membrane has pore-size distribution as follows: d(pore)0.33 fraction¼ 1.5 mm, d(pore)0.33 fraction¼ 1.0 mm, and d(pore)0.33 fraction¼ 0.5 mm. Required (a) Determine the distribution of flux density for each pore size. (b) Show by a plot the distribution of pore sizes and the distribution of flux density. solvearrow_forwardPlease show me your steps please thank you.arrow_forward
- Please show your work thanks.arrow_forwardA pipe 1.2 m diameter and 20 km long transmits water of velocity of 2 m/s. The friction coefficient of pipe is 0.007. Calculate the head loss due to friction?arrow_forwardA gas pipeline, NPS 20 with 0.500 in. wall thickness, transports natural gas (specific gravity = 0.6) at a flow rate of 250 MMSCFD at an inlet temperature of 60°F. Assuming isothermal flow, calculate the velocity of gas at the inlet and outlet of the pipe if the inlet pressure is 1000 psig and the outlet pressure is 850 psig. The base pressure and base temperature are 14.7 psia and 60°F, respectively. Assume compressibility factor Z = 1.00. What is the erosional velocity for this pipeline based on the above data and a compressibility factor Z = 0.90?arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





