Chapter 12.7, Problem 56E

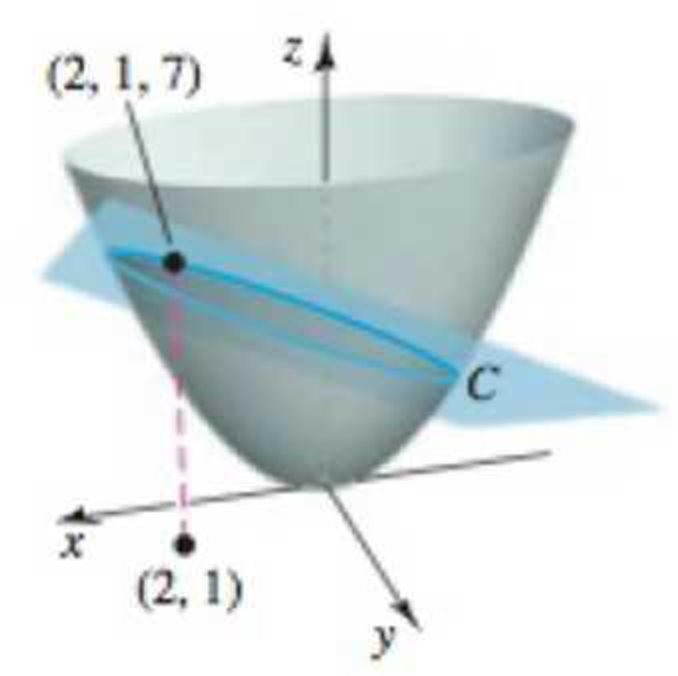
Line tangent to an intersection curve Consider the paraboloid z = x² + 3y² and the plane z = x + y + 4, which intersects the paraboloid in a curve C at (2, 1, 7) (see figure). Find the equation of the line tangent to C at the point (2.1, 7). Proceed as follows.

 a.    Find a vector normal to the plane at (2, 1, 7).

b.    Find a vector normal to the plane tangent to the paraboloid at (2,1,7).

c.    Argue that the line tangent to C at (2, 1, 7) is orthogonal to both normal vectors found in parts (a) and (b). Use this fact to find a direction vector for the tangent line.

d.    Knowing a point on the tangent line and the direction of the tangent line, write an equation of the tangent line in parametric form.