Chapter 12.6, Problem 94RP

Methane is to be adiabatically and reversibly compressed from 50 psia and 100°F to 500 psia. Calculate the specific work required for this compression treating the methane as an ideal gas with variable specific heats and using the departure charts.

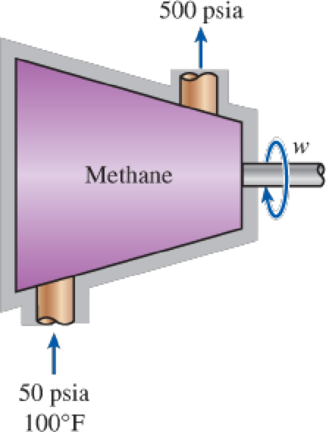
FIGURE P12–96E

To determine

The work input of the compressor per unit mass by treating the methane as an ideal gas with variable specific heats and using departure charts.

Answer to Problem 94RP

The work input of the compressor per unit mass by treating the methane as an ideal gas with variable specific heats is $205.1\text{Btu/lbm}$.

The work input of the compressor per unit mass of the methane using departure charts is $202.3\text{Btu/lbm}$.

Explanation of Solution

Refer the table A-2E (c), “Ideal gas specific heats of various common gases”.

The general empirical correlation is ${\overline{c}}_P=a+bT+c{T}^2+d{T}^3$.

Write the formula for enthalpy change in molar basis at ideal gas state ${\left({\overline{h}}_2-{\overline{h}}_1\right)}_{\text{ideal}}$.

$\begin{array}{c}{\left({\overline{h}}_2-{\overline{h}}_1\right)}_{\text{ideal}}={\displaystyle \underset{T_1}{\overset{T_2}{\int }}{c}_{P}dT}\\ ={\displaystyle \underset{T_1}{\overset{T_2}{\int }}\left(a+bT+c{T}^2+d{T}^3\right)dT}\\ ={\left[aT+\frac{b}{2}{T}^2+\frac{c}{3}{T}^3+\frac{d}{4}{T}^4\right]}_{T_1}^{T_2}\\ =a\left(T_2-T_1\right)+\frac{b}{2}\left(T_2^2-T_1^2\right)+\frac{c}{3}\left(T_2^3-T_1^3\right)+\frac{d}{4}\left(T_2^4-T_1^4\right)\end{array}$ (I)

Here, specific heat capacity at constant pressure is $c_P$, initial temperature is $T_1$, final temperature is $T_2$, the empirical constants are $a$, $b$, $c$, and $d$.

Write the formula for work input to the compressor $\left(w_{in}\right)$.

$w_{in}=\frac{{\left({\overline{h}}_2-{\overline{h}}_1\right)}_{\text{ideal}}}{M}$ (II)

Here, molar mass of methane is $M$.

Write the formula for entropy change in molar basis at ideal gas state ${\left({\overline{s}}_2-{\overline{s}}_1\right)}_{\text{ideal}}$.

$\begin{array}{c}{\left({\overline{s}}_2-{\overline{s}}_1\right)}_{\text{ideal}}={\displaystyle \underset{T_1}{\overset{T_2}{\int }}\frac{c_P}{T}dT}-R_u\ln \left(\frac{P_2}{P_1}\right)\\ =={\displaystyle \underset{T_1}{\overset{T_2}{\int }}\left(\frac{a}{T}+b+cT+d{T}^2\right)dT}-R_u\ln \left(\frac{P_2}{P_1}\right)\\ ={\left[a\ln \left(T\right)+bT+\frac{c}{2}{T}^2+\frac{d}{3}{T}^3\right]}_{T_1}^{T_2}-R_u\ln \left(\frac{P_2}{P_1}\right)\\ =a\ln \left(\frac{T_2}{T_1}\right)+b\left(T_2^{}-T_1^{}\right)+\frac{c}{2}\left(T_2^2-T_1^2\right)+\frac{d}{3}\left(T_2^3-T_1^3\right)-R_u\ln \left(\frac{P_2}{P_1}\right)\end{array}$ (III)

Here, universal gas constant is $R_u$, initial pressure is $P_2$, and final pressure is $P_2$.

Calculate the reduced temperature $\left(T_{R1}\right)$ at initial state.

$T_{R1}=\frac{T_1}{T_{\text{cr}}}$ (IV)

Here, critical temperature is $T_{\text{cr}}$ and initial temperature is $T_1$.

Calculate the reduced pressure $\left(P_{R1}\right)$ at initial state.

$P_{R1}=\frac{P_1}{P_{\text{cr}}}$ (V)

Here, critical pressure is $P_{\text{cr}}$ and initial pressure is $P_1$.

Calculate the reduced temperature $\left(T_{R2}\right)$ at final state.

$T_{R2}=\frac{T_2}{T_{\text{cr}}}$ (VI)

Here, critical temperature is $T_{\text{cr}}$ and final temperature is $T_2$.

Calculate the reduced pressure $\left(P_{R2}\right)$ at final state.

$P_{R2}=\frac{P_2}{P_{\text{cr}}}$ (VII)

Here, critical pressure is $P_{\text{cr}}$ and final pressure is $P_2$.

Write the formula for change in enthalpy $\left(h_2-h_1\right)$ using generalized enthalpy departure chart relation.

$h_2-h_1=\frac{{\left(h_2-h_1\right)}_{\text{ideal}}}{M}-R{T}_{\text{cr}}\left(Z_{h2}-Z_{h1}\right)$ (VIII)

Here, change in enthalpy of ideal gas is ${\left(h_2-h_1\right)}_{\text{ideal}}$, gas constant of methane is $R$, the enthalpy departure factor is $Z_h$, and the subscripts 1 and 2 indicates initial and final states.

Refer Table A-1E, “Molar mass, gas constant, and critical-point properties”.

The critical temperature and critical pressure of the methane is as follows.

$\begin{array}{l}{T}_{\text{cr}}=343.9\text{R}\\ P_{\text{cr}}=673\text{psia}\end{array}$

Refer table A-1E, “Molar mass, gas constant and critical properties table”.

The molar mass $\left(M\right)$ methane is $16.043\text{lbm/lbmol}$.

Refer the table A-2E (c), “Ideal gas specific heats of various common gases”.

Obtain the empirical constants as follows.

$\begin{array}{l}a=4.750\\ b=0.6666\times {10}^{-2}\\ c=0.09352\times {10}^{-5}\\ d=-0.4510\times {10}^{-9}\end{array}$

Refer Table A-2E (a), “Ideal-gas specific heats of various common gases”.

The gas constant $\left(R\right)$ of methane is $0.1238\text{Btu/lbm}\cdot \text{R}$ or $0.6688\text{psia}\cdot {\text{ft}}^3\text{/lbm}\cdot \text{R}$.

The specific heat at constant pressure $\left(c_p\right)$ of methane is $0.532\text{Btu/lbm}\cdot \text{R}$.

The universal gas constant $\left(R_u\right)$ is $1.9858\text{Btu/lbmol}\cdot \text{R}$.

Conclusion:

Convert the inlet temperature from degree Fahrenheit to Rankine.

$\begin{array}{c}{T}_1=100°\text{F}+460\\ =560\text{R}\end{array}$

It is given that the compression process in reversible adiabatic process. Hence, the change in entropy during the process is zero.

${\left({\overline{s}}_2-{\overline{s}}_1\right)}_{\text{ideal}}=0$

Substitute $0$ for ${\left({\overline{s}}_2-{\overline{s}}_1\right)}_{\text{ideal}}$, $4.75$ for $a$, $560\text{R}$ for $T_1$, $0.6666\times {10}^{-2}$ for $b$, $0.09352\times {10}^{-5}$ for $c$, $-0.4510\times {10}^{-9}$ for $d$, $500\text{psia}$ for $P_2$, $50\text{psia}$ for $P_1$, and $1.9858\text{Btu/lbmol}\cdot \text{R}$ for $R_u$ in Equation (III).

$\begin{array}{c}0=\left\{\begin{array}{l}\left(4.75\right)\ln \left(\frac{T_2}{560\text{R}}\right)+0.6666\times {10}^{-2}\left[\left(T_2\right)-\left(560\text{R}\right)\right]\\ +\frac{0.09352\times {10}^{-5}}{2}\left[{\left(T_2\right)}^2-{\left(560\text{R}\right)}^2\right]\\ +\frac{-0.4510\times {10}^{-9}}{3}\left[{\left(T_2\right)}^3-{\left(560\text{R}\right)}^3\right]\\ -\left(1.9858\text{Btu/lbmol}\cdot \text{R}\right)\ln \left(\frac{500\text{psia}}{50\text{psia}}\right)\end{array}\right\}\\ 0=\left\{\begin{array}{c}4.75\ln \frac{T_2}{560}+0.006666\left(T_2-560\right)+\frac{0.09352\times {10}^{-5}}{2}\left(T_2{}^2-{560}^2\right)\\ -\frac{0.4510\times {10}^{-9}}{3}\left(T_2{}^3-{560}^3\right)-4.5725\end{array}\right\}\end{array}$ (XI)

By using Engineering Equation Solver (EES) or online calculator to solve the Equation (XI) and obtain the value of $T_2$.

$T_2=892\text{R}$

Substitute $4.75$ for $a$,$892\text{R}$ for $T_2$, $560\text{R}$ for $T_1$, $0.6666\times {10}^{-2}$ for $b$, $0.09352\times {10}^{-5}$ for $c$, and $-0.4510\times {10}^{-9}$ for $d$ Equation (I).

$\begin{array}{c}{\left({\overline{h}}_2-{\overline{h}}_1\right)}_{\text{ideal}}=\left\{\begin{array}{l}4.75\left(892\text{R}-560\text{R}\right)+\frac{0.6666\times {10}^{-2}}{2}\left[{\left(892\text{R}\right)}^2-{\left(560\text{R}\right)}^2\right]+\\ \frac{0.09352\times {10}^{-5}}{3}\left[{\left(892\text{R}\right)}^3-{\left(560\text{R}\right)}^3\right]+\frac{-0.4510\times {10}^{-9}}{4}\left[{\left(892\text{R}\right)}^4-{\left(560\text{R}\right)}^4\right]\end{array}\right\}\\ =1577+1606.7193+166.5018-60.2915\\ =3289.9296\text{Btu/lbmol}\\ \simeq 3290\text{Btu/lbmol}\end{array}$

Substitute $3290\text{Btu/lbmol}$ for ${\left({\overline{h}}_2-{\overline{h}}_1\right)}_{\text{ideal}}$ and $16.043\text{lbm/lbmol}$ for $M$ in Equation (II)

$\begin{array}{c}{w}_{\text{in}}=\frac{3290\text{Btu/lbmol}}{16.043\text{lbm/lbmol}}\\ =205.0738\text{Btu/lbm}\\ \simeq 205.1\text{Btu/lbm}\end{array}$

Thus, the work input of the compressor per unit mass by treating the methane as an ideal gas with variable specific heats is $205.1\text{Btu/lbm}$.

Substitute $560\text{R}$ for $T_1$ and $343.9\text{R}$ for $T_{\text{cr}}$ in Equation (IV).

$\begin{array}{c}{T}_{R1}=\frac{560\text{R}}{343.9\text{R}}\\ =1.628\end{array}$

Substitute $50\text{psia}$ for $P_1$ and $673\text{psia}$ for $P_{\text{cr}}$ in Equation (V).

$\begin{array}{c}{P}_{R1}=\frac{50\text{psia}}{673\text{psia}}\\ =0.0743\end{array}$

Refer Figure A-29, “Generalized enthalpy departure chart”.

The enthalpy departure factor $\left(Z_{h1}\right)$ corresponding the reduced pressure $\left(P_{R1}\right)$ and reduced temperature $\left(T_{R1}\right)$ is $0.0332$.

Consider the final temperature $\left(T_2\right)$ is $892\text{R}$.

Substitute $892\text{R}$ for $T_2$ and $343.9\text{R}$ for $T_{cr}$ in Equation (VI).

$\begin{array}{c}{T}_{R2}=\frac{892\text{R}}{343.9\text{R}}\\ =2.594\end{array}$

Substitute $500\text{psia}$ for $P_2$ and $673\text{psia}$ for $P_{\text{cr}}$ in Equation (VII).

$\begin{array}{c}{P}_{R2}=\frac{500\text{psia}}{673\text{psia}}\\ =0.743\end{array}$

Refer Figure A-29, “Generalized enthalpy departure chart”.

The enthalpy departure factor $\left(Z_{h2}\right)$ corresponding the reduced pressure $\left(P_{R2}\right)$ and reduced temperature $\left(T_{R2}\right)$ is $0.0990$.

Substitute $3290\text{Btu/lbmol}$ for ${\left(h_2-h_1\right)}_{\text{ideal}}$,$16.043\text{lbm/lbmol}$ for $M$, $0.0990$ for $Z_{h2}$, $0.0332$ for $Z_{h1}$, $0.1238\text{Btu/lbm}\cdot \text{R}$ for $R$, and $343.9\text{R}$ for $T_{\text{cr}}$ in Equation (VIII).

$\begin{array}{c}{h}_2-h_1=\frac{3290\text{Btu/lbmo}}{16.043\text{lbm/lbmol}}\text{l}-\left(0.1238\text{Btu/lbm}\cdot \text{R}\right)\left(343.9\text{R}\right)\left(0.0990-0.0332\right)\\ =205.1\text{Btu/lbm}-2.8014\text{Btu/lbm}\\ =202.2985\text{Btu/lbm}\\ \simeq 202.3\text{Btu/lbm}\end{array}$

Here, the work input of the compressor is equal to the enthalpy difference.

$\begin{array}{c}{w}_{\text{in}}=h_2-h_1\\ =202.3\text{Btu/lbm}\end{array}$

Thus, the work input of the compressor per unit mass of the methane using departure charts is $202.3\text{Btu/lbm}$.