Skip to main content

Math Calculus EBK CALCULUS EARLY TRANSCENDENTALS SING

In each part, sketch the unit tangent and normal vectors at the points P , Q, and R , taking into account the orientation of the curve C.

In each part, sketch the unit tangent and normal vectors at the points P , Q, and R , taking into account the orientation of the curve C.

EBK CALCULUS EARLY TRANSCENDENTALS SING

EBK CALCULUS EARLY TRANSCENDENTALS SING

11th Edition

ISBN: 8220102011618

Author: Davis

Publisher: YUZU

See similar textbooks

Videos

Textbook Question

Chapter 12.4, Problem 1ES

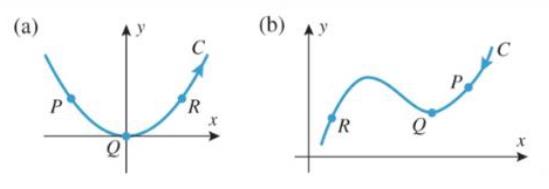
In each part, sketch the unit tangent and normal vectors at the points P, Q, and R, taking into account the orientation of the curve C.

Chapter 12.4, Problem 1ES, In each part, sketch the unit tangent and normal vectors at the points P, Q, and R, taking into

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

Blurred answer

Chapter 12.4, Problem 4QCE

Chapter 12.4, Problem 2ES

Students have asked these similar questions

Consider the following scenario. A pilot is steering a plane in the direction N 45° W at an air-speed (speed still in air) of 150 mi/h. A wind is blowing in the direction S 30° E at a speed of 34 mi/h. Set up the coordinate axes so that north is the positive y-direction and west is the negative x-direction. With respect to the still air, write a vector that represents the velocity of the plane and a vector that represents the velocity of the wind.

3m A. Find the unit vector that makes an angle (0 = - with the positive x-axis.

Find the angle between vector [2, −5,7] and the x-axis

Chapter 12 Solutions

EBK CALCULUS EARLY TRANSCENDENTALS SING

Ch. 12.1 - Prob. 1QCE Ch. 12.1 - Describe the graph of rt=1+2t,1+3t.Ch. 12.1 - Prob. 3QCE Ch. 12.1 - Prob. 4QCE Ch. 12.1 - Find the domain of rt and the value of rt0....Ch. 12.1 - Find the domain of rt and the value of rt0....Ch. 12.1 - Find the domain of rt and the value of rt0....Ch. 12.1 - Find the domain of rt and the value of rt0....Ch. 12.1 - Prob. 5ES Ch. 12.1 - Prob. 6ES

Ch. 12.1 - Prob. 7ES Ch. 12.1 - Prob. 8ES Ch. 12.1 - Describe the graph of the equation. r=32ti+5tj Ch. 12.1 - Describe the graph of the equation....Ch. 12.1 - Describe the graph of the equation. r=2ti3j+1+3tk Ch. 12.1 - Prob. 12ES Ch. 12.1 - Describe the graph of the equation....Ch. 12.1 - Describe the graph of the equation. r=3i+1t2j+tk Ch. 12.1 - (a) Find the slope of the line in 2-space that is...Ch. 12.1 - (a) Find the y-intercept of the line in 2-space...Ch. 12.1 - Prob. 17ES Ch. 12.1 - Sketch the line segment represented by each vector...Ch. 12.1 - Write a vector equation for the line segment from...Ch. 12.1 - Write a vector equation for the line segment from...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Sketch the graph of rt and show the direction of...Ch. 12.1 - Prob. 31ES Ch. 12.1 - Prob. 32ES Ch. 12.1 - Determine whether the statement is true or false....Ch. 12.1 - Determine whether the statement is true or false....Ch. 12.1 - Sketch the curve of intersection of the surfaces,...Ch. 12.1 - Sketch the curve of intersection of the surfaces,...Ch. 12.1 - Sketch the curve of intersection of the surfaces,...Ch. 12.1 - Prob. 38ES Ch. 12.1 - Show that the graph of r=tsinti+tcostj+t2k lies on...Ch. 12.1 - Show that the graph of r=ti+1+ttj+1t2tk,t0 lies in...Ch. 12.1 - Prob. 41ES Ch. 12.1 - Show that the graph of r=3costi+3sintj+3sintk is...Ch. 12.1 - Prob. 43ES Ch. 12.1 - How many revolutions will the circular helix...Ch. 12.1 - Show that the curve r=tcosti+tsintj+tk,t0, lies on...Ch. 12.1 - Describe the curve r=acosti+bsintj+ctk, where...Ch. 12.1 - In each part, match the vector equation with one...Ch. 12.1 - (a) Find parametric equations for the curve of...Ch. 12.1 - (a) Sketch the graph of rt=2t,21+t2 (b) Prove that...Ch. 12.1 - Prob. 51ES Ch. 12.1 - Suppose that r1tandr2t are vector-valued functions...Ch. 12.2 - alimt3t2i+2tj=blimt/4cost,sint=Ch. 12.2 - Find r t. art=4+5ti+tt2jbrt=1t,tant,e2t Ch. 12.2 - Suppose that r10=3,2,1,r20=1,2,3,r 10=0,0,0,andr...Ch. 12.2 - a012t,t2,sintdt=bti3t2j+etkdt=Ch. 12.2 - Find the limit. limt+t2+13t2+2,1t Ch. 12.2 - Prob. 2ES Ch. 12.2 - Find the limit. limt2ti3j+t2k Ch. 12.2 - Prob. 4ES Ch. 12.2 - Determine whether rt is continuous at t=0. Explain...Ch. 12.2 - Determine whether rt is continuous at t=0. Explain...Ch. 12.2 - Sketch the circle rt=costi+sintj, draw the vector...Ch. 12.2 - Sketch the circle rt=costi+sintj, draw the vector...Ch. 12.2 - Find r t. rt=4icostj Ch. 12.2 - Find r t. rt=tan1ti+tcostjtk Ch. 12.2 - Prob. 11ES Ch. 12.2 - Prob. 12ES Ch. 12.2 - Prob. 13ES Ch. 12.2 - Find the vector rt0; then sketch the graph of rt...Ch. 12.2 - Find the vector rt0; then sketch the graph of rt...Ch. 12.2 - Prob. 16ES Ch. 12.2 - Use a graphing utility to generate the graph of rt...Ch. 12.2 - Use a graphing utility to generate the graph of rt...Ch. 12.2 - Find parametric equations of the line tangent to...Ch. 12.2 - Find parametric equations of the line tangent to...Ch. 12.2 - Find parametric equations of the line tangent to...Ch. 12.2 - Find parametric equations of the line tangent to...Ch. 12.2 - Prob. 23ES Ch. 12.2 - Find a vector equation of the line tangent to the...Ch. 12.2 - Prob. 25ES Ch. 12.2 - Prob. 26ES Ch. 12.2 - Letrt=costi+sintj+k.findalimt0rtr tblimt0rtr...Ch. 12.2 - Prob. 28ES Ch. 12.2 - Calculate ddtr1tr2tandddtr1tr2t first by...Ch. 12.2 - Calculate ddtr1tr2tandddtr1tr2t first by...Ch. 12.2 - Evaluate the indefinite integral. 3i+4tjdt Ch. 12.2 - Evaluate the indefinite integral. t2i2tj+1tkdt Ch. 12.2 - Evaluate the indefinite integral. tet,lntdt Ch. 12.2 - Evaluate the indefinite integral. et,et,3t2dt Ch. 12.2 - Evaluate the definite integral. 0/2cos2t,sin2tdt Ch. 12.2 - Evaluate the definite integral. 01t2i+t3jdt Ch. 12.2 - Evaluate the definite integral. 02ti+t2jdt Ch. 12.2 - Evaluate the definite integral. 333t3/2,3+t3/2,1dt Ch. 12.2 - Evaluate the definite integral. 19t1/2i+t1/2jdt Ch. 12.2 - Evaluate the definite integral. 01e2ti+etj+tkdt Ch. 12.2 - Prob. 41ES Ch. 12.2 - Determine whether the statement is true or false....Ch. 12.2 - Prob. 43ES Ch. 12.2 - Prob. 44ES Ch. 12.2 - Solve the vector initial-value problem for yt by...Ch. 12.2 - Solve the vector initial-value problem for yt by...Ch. 12.2 - Solve the vector initial-value problem for yt by...Ch. 12.2 - Solve the vector initial-value problem for yt by...Ch. 12.2 - (a) Find the points where the curve r=ti+t2j3tk...Ch. 12.2 - Find where the tangent line to the curve...Ch. 12.2 - Show that the graphs of r1tandr2t intersect at the...Ch. 12.2 - Show that the graphs of r1tandr2t intersect at the...Ch. 12.2 - Use Formula (7) to derive the differentiation...Ch. 12.2 - Let u=ut,v=vt,andw=wt be differentiable...Ch. 12.2 - Let u1,u2,u3,1,2,3,w1,w2,andw3, be differentiable...Ch. 12.2 - Prove Theorem 12.2.6 for 2-space.Ch. 12.2 - Derive Formulas (6) and (7) for 3-space.Ch. 12.2 - Prove Theorem 12.2.9 for 2-space.Ch. 12.2 - Prob. 59ES Ch. 12.2 - Prob. 60ES Ch. 12.3 - If rt is a smooth vector-valued function, then the...Ch. 12.3 - If r(s) is a smooth vector-valued function...Ch. 12.3 - If rt is a smooth vector-valued function, then the...Ch. 12.3 - Suppose that rt is a smooth vector-valued function...Ch. 12.3 - Determine whether rt is a smooth function of the...Ch. 12.3 - Determine whether rt is a smooth function of the...Ch. 12.3 - Determine whether rt is a smooth function of the...Ch. 12.3 - Determine whether rt is a smooth function of the...Ch. 12.3 - Find the arc length of the parametric curve....Ch. 12.3 - Find the arc length of the parametric curve....Ch. 12.3 - Find the arc length of the parametric curve....Ch. 12.3 - Find the arc length of the parametric curve....Ch. 12.3 - Find the arc length of the graph of rt....Ch. 12.3 - Find the arc length of the graph of rt....Ch. 12.3 - Find the arc length of the graph of rt....Ch. 12.3 - Find the arc length of the graph of rt....Ch. 12.3 - Calculate dr/d by the chain rule, and then check...Ch. 12.3 - Calculate dr/d by the chain rule, and then check...Ch. 12.3 - Calculate dr/d by the chain rule, and then check...Ch. 12.3 - Calculate dr/d by the chain rule, and then check...Ch. 12.3 - Prob. 17ES Ch. 12.3 - Prob. 18ES Ch. 12.3 - Prob. 19ES Ch. 12.3 - Prob. 20ES Ch. 12.3 - (a) Find the arc length parametrization of the...Ch. 12.3 - Find arc length parametrizations of the lines in...Ch. 12.3 - Prob. 23ES Ch. 12.3 - (a) Find the arc length parametrization of the...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Find an arc length parametrization of the curve...Ch. 12.3 - Show that the arc length of the circular helix...Ch. 12.3 - Use the result in Exercise 31 to show the circular...Ch. 12.3 - Find an arc length parametrization of the cycloid...Ch. 12.3 - Show that in cylindrical coordinates a curve given...Ch. 12.3 - In each part, use the formula in Exercise 34 to...Ch. 12.3 - Show That in spherical coordinates a curve given...Ch. 12.3 - In each part, use the formula in Exercise 36 to...Ch. 12.3 - h (a) Sketch the graph of rt=ti+t2j. Show that rt...Ch. 12.3 - Find a change of parameter t=g for the semicircle...Ch. 12.3 - What change of parameter t=g would you make if you...Ch. 12.3 - As illustrated in the accompanying figure, copper...Ch. 12.3 - Let rt=cost,sint,t3/2.Findartbdsdtc02rtdt.Ch. 12.3 - Let rt=lnti+2tj+t2k.Findartbdsdtc13rtdt.Ch. 12.3 - Let rt=t2i+t3j (seeFigure12.3.1) . Let t be the...Ch. 12.3 - Prove: If rt is a smoothly parametrized function,...Ch. 12.3 - Prove the vector form of the chain rule for...Ch. 12.3 - Prob. 47ES Ch. 12.4 - Prob. 1QCE Ch. 12.4 - If C is the graph of a smooth vector-valued...Ch. 12.4 - If C is the graph of a smooth vector-valued...Ch. 12.4 - Suppose that C is the graph of a smooth...Ch. 12.4 - In each part, sketch the unit tangent and normal...Ch. 12.4 - Make a rough sketch that shows the ellipse...Ch. 12.4 - In the marginal note associated with Example 8 of...Ch. 12.4 - Use the result in Exercise 3 to show that the...Ch. 12.4 - Find TtandNt at the given point. rt=t21i+tj;t=1 Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Find TtandNt at the given point. rt=lnti+tj;t=e Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Find TtandNt at the given point....Ch. 12.4 - Use the result in Exercise 3 to find parametric...Ch. 12.4 - Use the result in Exercise 3 to find parametric...Ch. 12.4 - Use the formula Bt=TtNt to find Bt, and then check...Ch. 12.4 - Use the formula Bt=TtNt to find Bt, and then check...Ch. 12.4 - Use the formula Bt=TtNt to find Bt, and then check...Ch. 12.4 - Prob. 18ES Ch. 12.4 - Find Tt,Nt,andBt for the given value of t. Then...Ch. 12.4 - Find Tt,Nt,andBt for the given value of t. Then...Ch. 12.4 - Prob. 21ES Ch. 12.4 - Prob. 22ES Ch. 12.4 - Determine whether the statement is true or false....Ch. 12.4 - Prob. 24ES Ch. 12.4 - Discuss some of the advantages of parametrizing a...Ch. 12.5 - If C is a smooth curve parametrized by arc length,...Ch. 12.5 - Let rt be a smooth vector-valued function with...Ch. 12.5 - Suppose that C is the graph of a smooth...Ch. 12.5 - Suppose that C is a smooth curve and that x2+y2=4...Ch. 12.5 - Use the osculating circle shown in the figure to...Ch. 12.5 - Use the osculating circle shown in the figure to...Ch. 12.5 - For a plane curve y=fx the curvature at x,fx is...Ch. 12.5 - For a plane curve y=fx the curvature at x,fx is...Ch. 12.5 - Use Formula (3) to find t. rt=t2i+t3j Ch. 12.5 - Use Formula (3) to find t. rt=4costi+sintj Ch. 12.5 - Use Formula (3) to find t. rt=e3ti+etj Ch. 12.5 - Use Formula (3) to find t. x=1t3,y=tt2 Ch. 12.5 - Use Formula (3) to find t. rt=4costi+4sintj+tk Ch. 12.5 - Prob. 10ES Ch. 12.5 - Use Formula (3) to find t. x=cosht,y=sinht,z=t Ch. 12.5 - Use Formula (3) to find t. rt=i+tj+t3k Ch. 12.5 - Find the curvature and the radius of curvature at...Ch. 12.5 - Find the curvature and the radius of curvature at...Ch. 12.5 - Find the curvature and the radius of curvature at...Ch. 12.5 - Find the curvature and the radius of curvature at...Ch. 12.5 - Confirm that s is an arc length parameter by...Ch. 12.5 - Confirm that s is an arc length parameter by...Ch. 12.5 - Determine whether the statement is true or false....Ch. 12.5 - Determine whether the statement is true or false....Ch. 12.5 - Determine whether the statement is true or false....Ch. 12.5 - Determine whether the statement is true or false....Ch. 12.5 - (a) Use Formula (3) to show that in 2-space the...Ch. 12.5 - Use part (b) of Exercise 23 to show that the...Ch. 12.5 - Use the result in Exercise 23(b) to find the...Ch. 12.5 - Use the result in Exercise 23(b) to find the...Ch. 12.5 - Use the result in Exercise 23(b) to find the...Ch. 12.5 - Use the result in Exercise 23(b) to find the...Ch. 12.5 - Use the result in Exercise 23(a) to find the...Ch. 12.5 - Use the result in Exercise 23(a) to find the...Ch. 12.5 - Use the result in Exercise 23(a) to find the...Ch. 12.5 - Use the result in Exercise 23(a) to find the...Ch. 12.5 - In each part, use the formulas in Exercise 23 to...Ch. 12.5 - Prob. 34ES Ch. 12.5 - Generate the graph of y=fx using a graphing...Ch. 12.5 - Generate the graph of y=fx using a graphing...Ch. 12.5 - Prob. 37ES Ch. 12.5 - (a) Use a CAS to graph the parametric curve...Ch. 12.5 - Use the formula in Exercise 23 (a) to show that...Ch. 12.5 - Use the result in Exercise 39 to show that a...Ch. 12.5 - Use the formula in Exercise 39 to find the...Ch. 12.5 - Use the formula in Exercise 39 to find the...Ch. 12.5 - Use the formula in Exercise 39 to find the...Ch. 12.5 - Use the formula in Exercise 39 to find the...Ch. 12.5 - Find the radius of curvature of the parabola...Ch. 12.5 - At what point(s) does y=ex have maximum curvature...Ch. 12.5 - At what point(s) does 4x2+9y2=36 have a minimum...Ch. 12.5 - Find the maximum and minimum values of the radius...Ch. 12.5 - Use the formula in Exercise 39 to show that the...Ch. 12.5 - Use the formula in Exercise 39 and a CAS to show...Ch. 12.5 - Prob. 51ES Ch. 12.5 - The evolute of a smooth parametric curve C in...Ch. 12.5 - These exercises are concerned with the problem of...Ch. 12.5 - These exercises are concerned with the problem of...Ch. 12.5 - These exercises are concerned with the problem of...Ch. 12.5 - These exercises are concerned with the problem of...Ch. 12.5 - These exercises are concerned with the problem of...Ch. 12.5 - Assume that s is an arc length parameter for a...Ch. 12.5 - Assume that s is an arc length parameter for a...Ch. 12.5 - Assume that s is an arc length parameter for a...Ch. 12.5 - Prob. 61ES Ch. 12.5 - (a) Use the chain rule and the first two...Ch. 12.5 - Use the formula in Exercise 62(d) to find the...Ch. 12.5 - Use the formula in Exercise 62(d) to find the...Ch. 12.5 - Use the formula in Exercise 62(d) to find the...Ch. 12.5 - Use the formula in Exercise 62(d) to find the...Ch. 12.5 - The accompanying figure is the graph of the radius...Ch. 12.6 - If r(t) is the position function of a particle,...Ch. 12.6 - If r(t) is the position function of a particle,...Ch. 12.6 - The tangential scalar component of acceleration is...Ch. 12.6 - The projectile motion model r(t)=12gt2+s0j+tv0...Ch. 12.6 - Prob. 1ES Ch. 12.6 - Prob. 2ES Ch. 12.6 - Prob. 3ES Ch. 12.6 - Prob. 4ES Ch. 12.6 - Find the velocity, speed, and acceleration at the...Ch. 12.6 - Find the velocity, speed, and acceleration at the...Ch. 12.6 - Find the velocity, speed, and acceleration at the...Ch. 12.6 - Find the velocity, speed, and acceleration at the...Ch. 12.6 - As illustrated in the accompanying figure, suppose...Ch. 12.6 - Suppose that a particle vibrates in such a way...Ch. 12.6 - What can you say about the trajectory of a...Ch. 12.6 - Prob. 12ES Ch. 12.6 - Suppose that the position vector of a particle...Ch. 12.6 - Prob. 14ES Ch. 12.6 - Suppose that the position function of a particle...Ch. 12.6 - Suppose that the position function of a particle...Ch. 12.6 - Prob. 17ES Ch. 12.6 - Use the given information to find the position and...Ch. 12.6 - Prob. 19ES Ch. 12.6 - Prob. 20ES Ch. 12.6 - Find to the nearest degree, the angle between v...Ch. 12.6 - Prob. 22ES Ch. 12.6 - (a) Suppose that at time t=t0 an electron has a...Ch. 12.6 - Suppose that the position function of a particle...Ch. 12.6 - Find the displacement and the distance travelled...Ch. 12.6 - Find the displacement and the distance travelled...Ch. 12.6 - Find the displacement and the distance travelled...Ch. 12.6 - Find the displacement and the distance traveled...Ch. 12.6 - The position vectors r1andr2 of two particles are...Ch. 12.6 - The position vectors r1andr2 of two particles are...Ch. 12.6 - Prob. 31ES Ch. 12.6 - Prob. 32ES Ch. 12.6 - Prob. 33ES Ch. 12.6 - The position function of a particle is given. Use...Ch. 12.6 - Prob. 35ES Ch. 12.6 - Prob. 36ES Ch. 12.6 - In these exercises v and a are given at a certain...Ch. 12.6 - In these exercises v and a are given at a certain...Ch. 12.6 - The speed v of a particle at an arbitrary time t...Ch. 12.6 - The speed v of a particle at an arbitrary time t...Ch. 12.6 - The nuclear accelerator at the Enrico Fermi...Ch. 12.6 - Prob. 42ES Ch. 12.6 - Prob. 43ES Ch. 12.6 - Use the given information and Exercise 23 of...Ch. 12.6 - Use the given information to find the normal...Ch. 12.6 - Use the given information to find the normal...Ch. 12.6 - Determine whether the statement is true or false....Ch. 12.6 - Determine whether the statement is true or false....Ch. 12.6 - Determine whether the statement is true or false....Ch. 12.6 - Determine whether the statement is true or false....Ch. 12.6 - Derive Formula (18) from Formula (14).Ch. 12.6 - An automobile travels at a constant speed around a...Ch. 12.6 - If an automobile of mass m rounds a curve, then...Ch. 12.6 - A Shell is fired from ground level with a muzzle...Ch. 12.6 - A rock is thrown downward from the top of a...Ch. 12.6 - Solve Exercise 55 assuming that the rock is thrown...Ch. 12.6 - A shell is to be fired from ground level at an...Ch. 12.6 - A shell, fired from ground level at an elevation...Ch. 12.6 - Find two elevation angles that will enable a...Ch. 12.6 - A ball rolls off a table 4 ft high while moving at...Ch. 12.6 - As illustrated in the accompanying figure, a fire...Ch. 12.6 - What is the minimum initial velocity that will...Ch. 12.6 - As shown in the accompanying figure on the next...Ch. 12.6 - As illustrated in the accompanying figure, a train...Ch. 12.6 - A shell is fired from ground level at an elevation...Ch. 12.6 - A shell is fired from ground level with an...Ch. 12.6 - At time t=0 a baseball that is 5 ft above the...Ch. 12.6 - Repeat Exercise 67, assuming that the ball leaves...Ch. 12.6 - At time t=0 a skier leaves the end of a ski jump...Ch. 12.6 - At time t=0 a projectile is fired from a height h...Ch. 12.6 - Prob. 71ES Ch. 12.7 - Let G denote the universal gravitational constant...Ch. 12.7 - Suppose that a mass m is in an orbit about a mass...Ch. 12.7 - For a planet in an elliptical orbit about the Sun,...Ch. 12.7 - Suppose that a mass m is an orbit about a mass M...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12.7 - In exercises that require numerical values, use...Ch. 12 - Prob. 1RE Ch. 12 - Describe the graph of the equation. r=23ti4tj Ch. 12 - Describe the graph of the equation....Ch. 12 - Describe the graph of the equation....Ch. 12 - Describe the graph of the equation. r=2i+tj+t21k Ch. 12 - Prob. 6RE Ch. 12 - Show that the graph of rt=tsinti+tj+tcostk lies on...Ch. 12 - Find parametric equations for the intersection of...Ch. 12 - In words, give a geometric description of the...Ch. 12 - Prob. 10RE Ch. 12 - Find parametric equations of the line tangent to...Ch. 12 - Suppose that r1tandr2t are smooth vector-valued...Ch. 12 - Evaluate costi+sintjdt.Ch. 12 - Evaluate 0/3cos3t,sin3tdt.Ch. 12 - Solve the vector initial-value problem...Ch. 12 - Solve the vector initial-value problem...Ch. 12 - Prob. 17RE Ch. 12 - Prob. 18RE Ch. 12 - Find the arc length parametrization of the line...Ch. 12 - Find an arc length parametrization of the curve...Ch. 12 - Prob. 21RE Ch. 12 - Find T0,N0,andB0 for the curve...Ch. 12 - State the definition of "curvature" and explain...Ch. 12 - Suppose that rt is a smooth curve with r 0=iandr...Ch. 12 - Find the curvature of the curve at the stated...Ch. 12 - Find the curvature of the curve at the stated...Ch. 12 - Find the curvature of the curve at the stated...Ch. 12 - Find the curvature of the curve at the stated...Ch. 12 - Suppose that rt is the position function of a...Ch. 12 - (a) What does Theorem 12.2.8 tell you about the...Ch. 12 - As illustrated in the accompanying figure on the...Ch. 12 - If a particle of mass m has uniform circular...Ch. 12 - At time t=0 a particle at the origin of an...Ch. 12 - Prob. 34RE Ch. 12 - Use Formula (23) in Section 12.7 and refer to...Ch. 12 - As illustrated in the accompanying figure, the...Ch. 12 - A player throws a ball with an initial speed of 60...

Additional Math Textbook Solutions

Find more solutions based on key concepts

The solution of the given equation

Pre-Algebra Student Edition

Continuity at a point Determine whether the following functions are continuous at a. Use the continuity checkli...

Calculus: Early Transcendentals (2nd Edition)

CHECK POINT I You deposit $1000 in a saving account at a bank that has a rate of 4%. a. Find the amount, A, of ...

Thinking Mathematically (6th Edition)

Bernoulli 2 Do these situations involve Bernoulli trials? Explain. You are rolling 5 dice and need to get at le...

Stats

Angular size A boat sails directly toward a 150-meter skyscraper that stands on the edge of a harbor. The angul...

Calculus: Early Transcendentals (2nd Edition)

14. News Source Based on data from a Harris Interactive survey, 40% of adults say that they prefer to get their...

Elementary Statistics (13th Edition)

Knowledge Booster

Background pattern image

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

Similar questions

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Text book image

Algebra & Trigonometry with Analytic Geometry

Algebra

ISBN:9781133382119

Author:Swokowski

Publisher:Cengage

Text book image

Trigonometry (MindTap Course List)

Trigonometry

ISBN:9781305652224

Author:Charles P. McKeague, Mark D. Turner

Publisher:Cengage Learning

Text book image

Trigonometry (MindTap Course List)

Trigonometry

ISBN:9781337278461

Author:Ron Larson

Publisher:Cengage Learning

SEE MORE TEXTBOOKS

Basic Differentiation Rules For Derivatives; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=IvLpN1G1Ncg;License: Standard YouTube License, CC-BY