
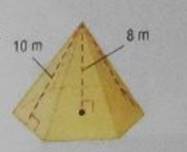
Find the Lateral area and surface area of the regular pyramid.
Answer to Problem 3CYU
L =
S =
Explanation of Solution
Given:
Formula Used: The Lateral area L of a regular Pyramid is
The Surface area S of a regular Pyramid is
Calculation:
The base of the pyramid is regular hexagon.As shown in the figure, find the base of the right
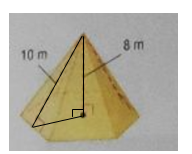
Using Pythagoras Theorem :
So, the length of the base b =
Now, the base is a regular hexagon .Divide the base in 6 equal
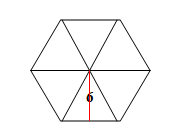
Draw the right angled triangle out and find the base:
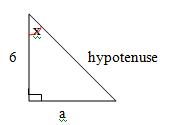
Now, first find the value of x =
Also,
Now, the length of base of each triangle =
Hence , each side of the hexagon is
Perimeter of the base = P = (length of each side )(number of sides ) =
So, the Lateral area =
The area of one section of the hexagon , which is a triangle with base
6 m is
So, the area of the base = B =
So, the surface area of the pyramid :
Hence ,
L =
S =
Chapter 12 Solutions
Geometry, Student Edition
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
University Calculus: Early Transcendentals (4th Edition)
A First Course in Probability (10th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
- 7. 11 m 12.7 m 14 m S V=B₁+ B2(h) 9.5 m 16 m h+s 2 na 62-19 = 37 +, M h² = Bu-29arrow_forwardwhat would a of a interscribed angle be with an arc of 93 degrees and inside abgles of 111 and 98arrow_forwardPlease complete through GeoGebra and present the screenshots of the results. Thanks! (This supports on how to submit it.)arrow_forward
- Door 87.5in to 47 living 44.75 Closet 96in Window ISS.Sin 48in Train Table 96in 48in 132:2 Windowarrow_forward39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

