Chapter 12.2, Problem 28E

a. Consider the data in Exercise 20. Suppose that instead of the least squares line passing through the points (x₁, y₁),…, (x_n, y_n) we wish the least squares line passing through $(x_1-\bar{x},y_1),\dots ,(x_n-\bar{x},y_n)$. Construct a scatterplot of the (x_i, y_i) points and then of the $(x_i-\bar{x},y_i)$ points. Use the plots to explain intuitively how the two least squares lines are related to one another.

b. Suppose that instead of the model Y_i = β₀ + β₁x_i + ϵ_i (i = 1,…, n), we wish to fit a model of the form $Y_i={\beta }_0^{*}+{\beta }_1^{*}(x_1-\bar{x})+{ϵ}_i$ (i = 1,…, n). What are the least squares estimators of ${\beta }_0^{*}$ and ${\beta }_1^{*}$, and how do they relate to ${\hat{\beta }}_0$ and ${\hat{\beta }}_1$?

To determine

Draw the scatterplot of the points $\left(x_i,y_i\right)$ corresponding to the variables ratio $\left(y\right)$ and pressure $\left(x\right)$.

Draw the scatterplot of the points $\left(x_i-\overline{x},y_i\right)$ corresponding to the variables ratio $\left(y\right)$ and pressure $\left(x\right)$.

Explain the relationship between the least squares lines using the scatterplot.

Answer to Problem 28E

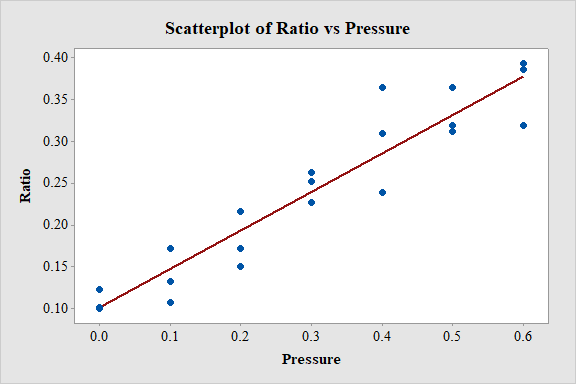
Scatter plot of $\left(x_i,y_i\right)$:

Output using MINITAB software is given below:

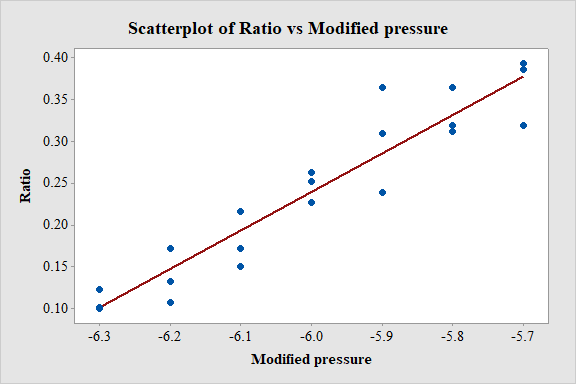
Scatter plot of $\left(x_i-\overline{x},y_i\right)$:

Output using MINITAB software is given below:

The slope of both the plots remains same.

Explanation of Solution

Given info:

The data represents the values of lateral pressure and the ratio of bond strength expressed in $f_{cu}$ and bond strength expressed in MPa for the reinforcing bars.

Justification:

Scatter plot of $\left(x_i,y_i\right)$:

Software Procedure:

Step by step procedure to obtain scatterplot using Minitab software is given as,

• Choose Graph > Scatter plot.
• Choose With regression, and then click OK.
• Under Y variables, enter a column of Ratio.
• Under X variables, enter a column of Pressure.
• Click Ok.

Observation:

From the scatterplot it is observed that, as the values of pressure increases the ratio also increases linearly. Thus, there is a positive association between the variables pressure and ratio.

Mean of the variable pressure:

The general formula to obtain mean is,

$\overline{x}=\frac{{\displaystyle \sum _i{x}_i}}{n}$.

The points $\left(x_i-\overline{x},y_i\right)$ are obtained as follows:

i	Ratio $\left(y_i\right)$	Pressure $\left(x_i\right)$	$\left(x_i-\overline{x}\right)$
1	0.123	0	-6.3
2	0.1	0	-6.3
3	0.101	0	-6.3
4	0.172	0.1	-6.2
5	0.133	0.1	-6.2
6	0.107	0.1	-6.2
7	0.217	0.2	-6.1
8	0.172	0.2	-6.1
9	0.151	0.2	-6.1
10	0.263	0.3	-6
11	0.227	0.3	-6
12	0.252	0.3	-6
13	0.31	0.4	-5.9
14	0.365	0.4	-5.9
15	0.239	0.4	-5.9
16	0.365	0.5	-5.8
17	0.319	0.5	-5.8
18	0.312	0.5	-5.8
19	0.394	0.6	-5.7
20	0.386	0.6	-5.7
21	0.32	0.6	-5.7
Total		${\displaystyle \sum _{\text{i=1}}^{\text{n}}{x}_i}=6.3$

The mean of pressure is,

$\begin{array}{c}\overline{x}=\frac{{\displaystyle \sum _{\text{i=1}}^{\text{n}}{x}_i}}{n}\\ =\frac{6.3}{21}\\ =0.3\end{array}$

Thus, the mean of pressure is $\overline{x}=0.3$.

Scatter plot of $\left(x_i-\overline{x},y_i\right)$:

Software Procedure:

Step by step procedure to obtain scatterplot using Minitab software is given as,

• Choose Graph > Scatter plot.
• Choose With regression, and then click OK.
• Under Y variables, enter a column of Ratio.
• Under X variables, enter a column of Modified pressure.
• Click Ok.

Observation:

From the scatterplot it is observed that, as the values of pressure increases the ratio also increases linearly. Thus, there is a positive association between the variables pressure and ratio.

Relationship between the two plots:

The slope of both the plots is same. By subtracting mean from the predictor variable the plot just shifts horizontally without affecting the characteristics.

The least squares line of the points $\left(x_i,y_i\right)$ passes through $\left(\overline{x},\overline{y}\right)$.

The least squares line of the points $\left(x_i-\overline{x},y_i\right)$ passes through $\left(0,\overline{y}\right)$.

To determine

Derive the least squares estimators of ${\beta }_0^{*}$ and ${\beta }_1^{*}$ of the regression model $Y_i={\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)+{\epsilon }_i$.

Explain the relationship between the least squares estimates of the regression line $Y_i={\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)++{\epsilon }_i$ and the least squares estimates of the regression line $Y_i={\beta }_0+{\beta }_1{x}_i+{\epsilon }_i$

Answer to Problem 28E

The least squares estimate of slope coefficient is ${\widehat{\beta }}_1^{*}={\widehat{\beta }}_1$.

The least squares estimate of intercept is ${\widehat{\beta }}_0^{*}=\overline{Y}$.

The slope coefficient is same for both the regression lines and the intercept changes.

Explanation of Solution

Calculation:

Least squares estimate:

In a linear equation $y=b_0+b_1{x}_i$ the constant $b_1$ be the slope and $b_0$ be the y-intercept form and x is the independent variable and y is the independent variable.

The error function for the equation is,

$f\left(b_0,b_1\right)={\displaystyle \sum _{i=1}^n{\left(y_i-\left(b_0+b_1{x}_i\right)\right)}^2}$

In the linear equation the point estimates of the $b_0$ and $b_1$ are ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$. These point estimates are the values that minimize the equation $f\left(b_0,b_1\right)$. That is, $f\left({\widehat{\beta }}_0,{\widehat{\beta }}_1\right)\le f\left(b_0,b_1\right)$.

Then the values of ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$ are the least squares estimates and the equation $\widehat{y}={\widehat{\beta }}_0+{\widehat{\beta }}_1{x}_i$

Here, in the equation $Y_i={\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)+{\epsilon }_i$ the least squares estimate of ${\beta }_0^{*}$ is ${\widehat{\beta }}_0^{*}$ and the least squares estimate of ${\beta }_1^{*}$ is ${\widehat{\beta }}_1^{*}$.

From the concept of least squares, the values of ${\widehat{\beta }}_0^{*}$ and ${\widehat{\beta }}_1^{*}$ are the values of ${\beta }_0^{*}$ and ${\beta }_1^{*}$ which minimizes the equation ${\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}$

Minima:

Let y be an objective function in terms of x. To obtain the value of x that minimizes the objective function, the first derivative of y with respect to x must be equalized to 0. Then the obtained value of x is considered as the value which minimizes the objective function y.

Least square estimates of intercept:

Here, the desired value of ${\beta }_0^{*}$ is obtained as follows:

Step1:

Obtaining the first derivative of ${\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}$ with respect to the constant ${\beta }_0^{*}$,

$\begin{array}{c}\frac{d}{d{\beta }_0^{*}}\left\{{\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}\right\}={\displaystyle \sum \frac{d}{d{\beta }_0^{*}}}{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2\\ =-2\times {\displaystyle \sum \left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}\\ =-2\times \left({\displaystyle \sum Y_i-{\displaystyle \sum {\beta }_0^{*}-{\displaystyle \sum {\beta }_1^{*}\left(x_i-\overline{x}\right)}}}\right)\\ =-2\times \left({\displaystyle \sum Y_i}-n{\beta }_0^{*}-{\beta }_1^{*}{\displaystyle \sum \left(x_i-\overline{x}\right)}\right)\end{array}$

Since, the mean acts as a balancing point for observations larger and smaller than it, the sum of the deviations around the mean is always zero.

That is, ${\displaystyle \sum \left(x_i-\overline{x}\right)}=0$.

Step2:

Equating the obtained derivate to “0”,

$\begin{array}{c}-2\times \left({\displaystyle \sum Y_i}-n{\beta }_0^{*}-{\beta }_1^{*}{\displaystyle \sum \left(x_i-\overline{x}\right)}\right)=0\\ \left({\displaystyle \sum Y_i}-n{\beta }_0^{*}-{\beta }_1^{*}\times 0\right)=0\\ {\displaystyle \sum Y_i}-n{\beta }_0^{*}=0\\ {\beta }_0^{*}=\frac{{\displaystyle \sum Y_i}}{n}\end{array}$

Thus, the least square estimates of intercept ${\beta }_0^{*}$ is ${\widehat{\beta }}_0^{*}=\frac{{\displaystyle \sum Y_i}}{n}=\overline{Y}$.

Least square estimates of slope:

Here, the desired value of ${\beta }_1^{*}$ is obtained as follows:

Step1:

Obtaining the first derivative of ${\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}$ with respect to the constant ${\beta }_1^{*}$,

$\begin{array}{c}\frac{d}{d{\beta }_1^{*}}\left\{{\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}\right\}={\displaystyle \sum \frac{d}{d{\beta }_1^{*}}}{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2\\ =2\times {\displaystyle \sum \left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)\left(-\left(x_i-\overline{x}\right)\right)}\\ =-2\times \left({\displaystyle \sum Y{\left(x_i-\overline{x}\right)}_i-{\displaystyle \sum \left(x_i-\overline{x}\right){\beta }_0^{*}-{\displaystyle \sum \left(x_i-\overline{x}\right){\beta }_1^{*}\left(x_i-\overline{x}\right)}}}\right)\\ =-2\times \left({\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)-{\displaystyle \sum \left(x_i-\overline{x}\right){\beta }_0^{*}}-{\beta }_1^{*}{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}\right)\end{array}$

Since, the mean acts as a balancing point for observations larger and smaller than it, the sum of the deviations around the mean is always zero.

That is, ${\displaystyle \sum \left(x_i-\overline{x}\right)}=0$.

Step2:

Equating the obtained derivate to “0”,

$\begin{array}{c}-2\times \left({\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)-{\displaystyle \sum \left(x_i-\overline{x}\right){\beta }_0^{*}}-{\beta }_1^{*}{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}\right)=0\\ \left({\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)-0\times {\beta }_0^{*}-{\beta }_1^{*}{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}\right)=0\\ {\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)-{\beta }_1^{*}{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}=0\\ {\beta }_1^{*}=\frac{{\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\end{array}$

Thus, the least square estimates of slope ${\beta }_1^{*}$ is ${\widehat{\beta }}_1^{*}=\frac{{\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}$.

Therefore, the quantity ${\displaystyle \sum _{i=1}^n{\left(Y_i-\left({\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)\right)\right)}^2}$ will be minimized for ${\widehat{\beta }}_0^{*}=\frac{{\displaystyle \sum Y_i}}{n}=\overline{Y}$ and ${\widehat{\beta }}_1^{*}=\frac{{\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}$.

Relationship:

The least squares estimates of the regression line $Y_i={\beta }_0^{*}+{\beta }_1^{*}\left(x_i-\overline{x}\right)+{\epsilon }_i$ are ${\widehat{\beta }}_0^{*}=\frac{{\displaystyle \sum Y_i}}{n}=\overline{Y}$ and ${\widehat{\beta }}_1^{*}=\frac{{\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}$.

Further simplification of ${\widehat{\beta }}_1^{*}$ is as follows:

$\begin{array}{c}{\widehat{\beta }}_1^{*}=\frac{{\displaystyle \sum Y_i}\left(x_i-\overline{x}\right)}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\\ =\frac{{\displaystyle \sum x_i{Y}_i-{\displaystyle \sum \overline{x}{Y}_i}}}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\\ =\frac{{\displaystyle \sum x_i{Y}_i-\left(\left({\displaystyle \sum Y_i}\right)\overline{x}\right)\frac{n}{n}}}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\\ =\frac{{\displaystyle \sum x_i{Y}_i-\left(\left(\frac{{\displaystyle \sum Y_i}}{n}\right)n\overline{x}\right)}}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\end{array}$

$\begin{array}{c}=\frac{{\displaystyle \sum x_i{Y}_i-\left(\left(\frac{{\displaystyle \sum Y_i}}{n}\right){\displaystyle \sum x_i}\right)}}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\\ =\frac{{\displaystyle \sum x_i{Y}_i-\frac{\left({\displaystyle \sum x_i}\right)\times \left({\displaystyle \sum Y_i}\right)}{n}}}{{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}}\\ =\frac{S_{xy}}{S_{xx}}\end{array}$

That is, ${\widehat{\beta }}_1^{*}=\frac{S_{xy}}{S_{xx}}$.

The least squares estimates of the regression line $Y_i={\beta }_0+{\beta }_1{x}_i+{\epsilon }_i$ are ${\widehat{\beta }}_0=\overline{y}-{\widehat{\beta }}_1\overline{x}$ and ${\widehat{\beta }}_1=\frac{S_{xy}}{S_{xx}}$.

Comparing both the estimates, the slope estimate of coefficient is same in both the cases and the estimate of intercept changes.