Chapter 12.4, Problem 48E

a.

To determine

Check whether a linear model is appropriate for the data using the scatterplot.

Answer to Problem 48E

Output using MINITAB software is given below:

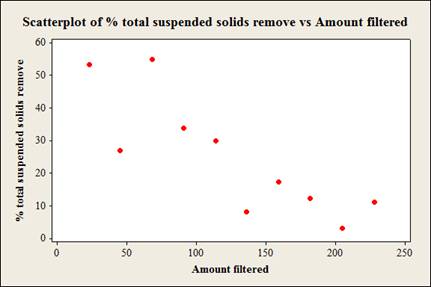
Yes, a simple linear model is appropriate for the data.

Explanation of Solution

Given info:

The data represents the values of the variables % total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$. The variable amount filtered is measured in 1000’s of liters.

Justification:

Software Procedure:

Step by step procedure to obtain scatterplot using MINITAB software is given as,

• Choose Graph > Scatter plot.
• Choose Simple, and then click OK.
• Under Y variables, enter a column of % Total suspended solids removed.
• Under X variables, enter a column of Amount filtered.
• Click Ok.

Observation:

From the scatterplot it is clear that, as the values of amount filtered increases the values of % total suspended solids removed decreases linearly. Thus, there is a negative association between the variables amount filtered and % total suspended solids removed.

Appropriateness of regression linear model:

The conditions for a scatterplot that is well fitted for the data are,

• Straight Enough Condition: The relationship between y and x straight enough to proceed with a linear regression model.
• Outlier Condition: No outlier must be there which influences the fit of the least square line.
• Thickness Condition: The spread of the data around the generally straight relationship seem to be consistent for all values of x.

The scatterplot shows a fair enough linear relationship between the variables amount filtered and % total suspended solids removed. The spread of the data seem to roughly consistent.

Moreover, the scatterplot does not show any outliers.

Therefore, all the three conditions of appropriateness of simple linear model are satisfied.

Thus, a linear model is appropriate for the data.

b.

To determine

Find the regression line for the variables % total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$.

Answer to Problem 48E

The regression line for the variables % total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$ is $\underset{\_}{\stackrel{⌢}{y}=52.6-0.220x}$.

Explanation of Solution

Calculation:

Linear regression model:

A linear regression model is given as $\widehat{y}=b_0+b_{1}x$ where be the predicted values of response variable and x be the predictor variable. The $b_1$ be the slope and $b_0$ be the intercept of the line.

A linear regression model is given as $\widehat{y}={\widehat{\beta }}_0+{\widehat{\beta }}_{1}x$ where $\widehat{y}$ be the predicted values of response variable and x be the predictor variable. The ${\widehat{\beta }}_1$ be the estimate of slope and ${\widehat{\beta }}_0$ be the estimate of intercept of the line.

In the given problem the % of total suspended solids remove is the response variable y and the amount filtered is the predictor variable x

Regression:

Software procedure:

Step by step procedure to obtain regression equation using MINITAB software is given as,

• Choose Stat > Regression > Fit Regression Line.
• In Response (Y), enter the column of Removal efficiency.
• In Predictor (X), enter the column of Inlet temperature.
• Click OK.

The output using MINITAB software is given as,

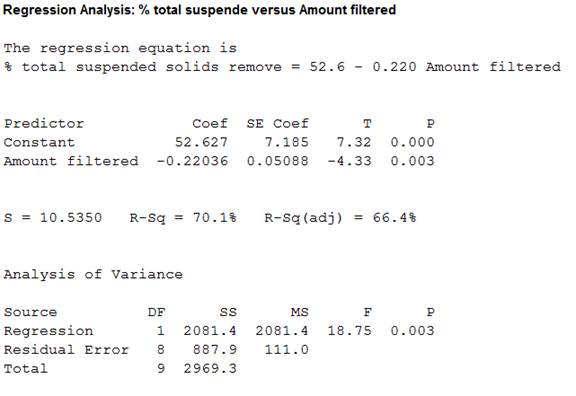
Thus, the regression line for the variables % total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$  is $\underset{\_}{\stackrel{⌢}{y}=52.6-0.220x}$.

Interpretation:

The slope estimate implies a decrease in % total suspended solids removed by 22.0% for every 1,000 liters increase in amount filtered. It can also be said that, for every 1% increase in amount filtered the % total suspended solids removed decreases 22%.

c.

To determine

Find the proportion of observed variation in % total suspended solids removed that can be explained by amount filtered using the simple linear regression model.

Answer to Problem 48E

The proportion of observed variation in % total suspended solids removed that can be explained by amount filtered using the simple linear regression model is $\underset{\_}{r^2=0.701}$.

Explanation of Solution

Justification:

$R^2$(R-squared):

The coefficient of determination ($R^2$) is defined as the proportion of variation in the observed values of the response variable that is explained by the regression. The squared correlation gives fraction of variability of response variable (y) accounted for by the linear regression model.

The general formula to obtain coefficient of variation is,

$R^2=r^2$

From the regression output obtained in part (b), the value of coefficient of determination is 0.701.

Thus, the coefficient of determination is $\underset{\_}{r^2=0.701}$.

Interpretation:

From this coefficient of determination it can be said that, the amount filtered can explain only 70.1% variability in % total suspended solids removed. Then remaining variability of % total suspended solids removed is explained by other variables.

Thus, the percentage of variation in the observed values of %total suspended solids removed that is explained by the regression is 70.1%, which indicates that 70.1% of the variability in %total suspended solids removed is explained by variability in the amount filtered using the linear regression model.

d.

To determine

Test whether there is enough evidence to conclude that the predictor variable amount filtered is useful for predicting the value of the response variable %total suspended solids removed at $\alpha =0.05$.

Answer to Problem 48E

There is sufficient evidence to conclude that the predictor variable amount filtered is useful for predicting the value of the response variable %total suspended solids removed.

Explanation of Solution

Calculation:

From the MINITAB output obtained in part (b), the regression line for the variables %total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$  is $\underset{\_}{\stackrel{⌢}{y}=52.6-0.220x}$.

The test hypotheses are given below:

Null hypothesis:

$H_0:{\beta }_1=0$

That is, there is no useful relationship between the variables %total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$.

Alternative hypothesis:

$H_1:{\beta }_1\ne 0$

That is, there is useful relationship between the variables %total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$.

T-test statistic:

The test statistic is,

$t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\sim t\left(n-2\right)$

From the MINITAB output obtained in part (b), the test statistic is -4.33 and the P-value is 0.003.

Thus, the value of test statistic is -4.33 and P-value is 0.003.

Level of significance:

Here, level of significance is $\alpha =0.05$.

Decision rule based on p-value:

If $P\text{-value}\le \alpha$, then reject the null hypothesis $H_0$.

If $P\text{-value}>\alpha$, then fail to reject the null hypothesis $H_0$.

Conclusion:

The P-value is 0.003 and $\alpha$ value is 0.05.

Here, P-value is less than the $\alpha$ value.

That is $0.003\left(=p\right)<0.05\left(=\alpha \right)$.

By the rejection rule, reject the null hypothesis.

Thus, there is sufficient evidence to conclude that the predictor variable amount filtered is useful for predicting the value of the response variable %total suspended solids removed.

e.

To determine

Test whether there is enough evidence to infer that the true average decrease in “%total suspended solids removed” associated with 10,000 liters increase in “amount filtered” is greater than or equal to 2 at $\alpha =0.05$.

Answer to Problem 48E

There is no sufficient evidence to infer that the true average decrease in “%total suspended solids removed” associated with 10,000 liters increase in “amount filtered” is greater than or equal to 2.

Explanation of Solution

Calculation:

Linear regression model:

A linear regression model is given as $\widehat{y}=b_0+b_{1}x$ where $\widehat{y}$ be the predicted values of response variable and x be the predictor variable. $b_1$ be the slope and $b_0$ be the intercept of the line.

A linear regression model is given as $\widehat{y}={\widehat{\beta }}_0+{\widehat{\beta }}_{1}x$ where $\widehat{y}$ be the predicted values of response variable and x be the predictor variable. The ${\widehat{\beta }}_1$ be the estimate of slope and ${\widehat{\beta }}_0$ be the estimate of intercept of the line.

From the MINITAB output in part (b), the slope coefficient of the regression equation is $b_1={\widehat{\beta }}_1=-0.22$.

Here, ${\widehat{\beta }}_1$ be the slope of the sample regression line and ${\beta }_1$ is the slope of the population regression line.

Here, the claim is that, when the amount filtered is increased from 10,000 liters the true average decrease in %total suspended solids removed is greater than or equal to 2.

The claim states that, amount filtered is increased by 10,000 liters.

Decrease in the %total suspended solids removed for 1,000 liters increase in amount filtered:

The true average decrease in the %total suspended solids removed for 1,000 liters increase in amount filtered is,

$\begin{array}{c}10,000\text{liters}=2\\ 1,000\text{liters}=\frac{2}{10}\\ =0.2\end{array}$

That is, when the amount filtered is increased by 1,000 liters the true average decrease in %total suspended solids removed is greater than or equal to 0.2.

The test hypotheses are given below:

Null hypothesis:

$H_0:{\beta }_1\ge -0.2$

That is, the true average decrease in %total suspended solids removed is greater than or equal to 0.2.

Alternative hypothesis:

$H_1:{\beta }_1<-0.2$

That is, the true average decrease in %total suspended solids removed is less than 0.2.

Test statistic:

The test statistic is,

$t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\sim t\left(n-2\right)$

Degrees of freedom:

The sample size is $n=10$

The degrees of freedom is,

$\begin{array}{c}d.f=10-2\\ =10-2\\ =8\end{array}$

Thus, the degree of freedom is 8.

Here, level of significance is $\alpha =0.05$.

Critical value:

Software procedure:

Step by step procedure to obtain the critical value using the MINITAB software:

• Choose Graph > Probability Distribution Plot choose View Probability > OK.
• From Distribution, choose ‘t’ distribution and enter 8 as degrees of freedom.
• Click the Shaded Area tab.
• Choose Probability Value and Left Tail for the region of the curve to shade.
• Enter the Probability value as 0.05.
• Click OK.

Output using the MINITAB software is given below:

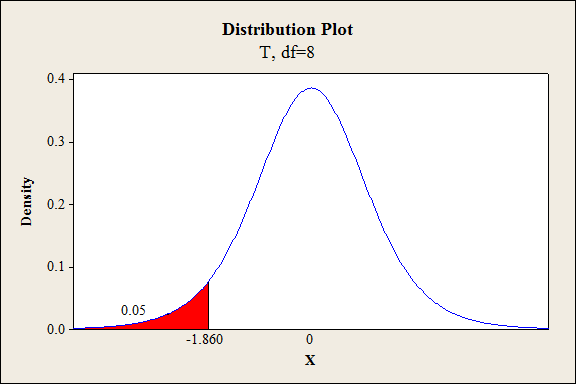
From the output, the critical value is –1.860.

Thus, the critical value is $\left(-t_{0.05,10}\right)=-1.860$.

From the MINITAB output obtained in part (b), the estimate of error standard deviation of slope coefficient is $s_{{\widehat{\beta }}_1}=0.05088$.

Test statistic under null hypothesis:

Under the null hypothesis, the test statistic is obtained as follows:

$\begin{array}{c}t=\frac{{\widehat{\beta }}_1-{\beta }_1}{s_{{\widehat{\beta }}_1}}\\ =\frac{-0.22-\left(-0.2\right)}{0.05088}\\ =-0.3931\end{array}$

Thus, the test statistic is -0.3931.

Decision criteria for the classical approach:

If $t<-t_{\alpha }\left(\text{test}\text{statistic}<\text{ critical}\text{value}\right)$, then reject the null hypothesis $\left(H_0\right)$.

Conclusion:

Here, the test statistic is -0.3931 and critical value is –1.860.

The t statistic is less than the critical value.

That is, $-0.3931\left(\text{=test statistic}\right)<-1.860\left(=\text{critical value}\right)$

Based on the decision rule, reject the null hypothesis.

Hence, the true average decrease in %total suspended solids removed is not greater than or equal to 0.2.

Therefore, there is no sufficient evidence to infer that the true average decrease in “%total suspended solids removed” associated with 10,000 liters increase in “amount filtered” is greater than or equal to 2.

f.

To determine

Find the 95% specified confidence interval for the true mean %total suspended solids removed when the amount filtered is 100,000 liters.

Compare the width of the confidence intervals for 100,000 liters and 200,000 liters amount filtered.

Answer to Problem 48E

The 95% specified confidence interval for the true mean %total suspended solids removed when the amount filtered is 100,000 liters is $\underset{\_}{\left(22.37244,38.82756\right)}$.

The confidence interval for 100,000 liters of amount filtered will be narrower than the interval for 200,000 liters of amount filtered.

Explanation of Solution

Calculation:

From the MINITAB output obtained in part (b), the regression line for the variables %total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$  is $\underset{\_}{\stackrel{⌢}{y}=52.6-0.220x}$.

Here, the variable amount filtered $\left(x\right)$ is measured in 1000’s of liters.

Hence, the value of 100,000 for amount filtered is $x=100$.

Expected %total suspended solids removed when the amount filtered is $x=100$:

The expected value of %total suspended solids removed with $x=100$ is obtained as follows:

$\begin{array}{c}{\widehat{\mu }}_{\widehat{y}}=52.6-0.220x\\ =52.6-0.220\times 100\\ =30.6\end{array}$

Thus, the expected value of %total suspended solids removed with $x=100$ is 30.6.

Confidence interval:

The general formula for the $\left(1-\alpha \right)$% confidence interval for the conditional mean at $x=x_p$ is,

$CI={\widehat{\mu }}_{\widehat{y}}\pm t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}$

Where, ${\widehat{y}}_p$ be the point estimate for the conditional mean of the response variable at $x=x_p$, and $S_{\text{xx}}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}$.

From the MINITAB output in part (a), the value of the standard error of the estimate is $s=10.5350$.

The value of $S_{\text{xx}}$ is obtained as follows:

From the give data, the sum of amount filtered is ${\displaystyle \sum x_i}=1,251$ and ${\displaystyle \sum x_i^2}=199,365$.

The mean amount filtered is,

$\begin{array}{c}\overline{x}=\frac{{\displaystyle \sum x_i}}{n}\\ =\frac{1,251}{10}\\ =125.1\end{array}$

Thus, the mean amount filtered is $\underset{\_}{\overline{x}=125.1}$.

Covariance term $S_{\text{xx}}$:

The value of $S_{\text{xx}}$ is,

$\begin{array}{c}{S}_{\text{xx}}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}\\ =199,365-\frac{{1251}^2}{10}\\ =199,365-156,500.1\\ =42,864.9\end{array}$

Thus, the covariance term $S_{\text{xx}}$ is 42,864.9.

Critical value:

For 95% confidence level,

$\begin{array}{c}1-\alpha =1-0.95\\ \alpha =0.05\\ \frac{\alpha }{2}=\frac{0.05}{2}\\ =0.025\end{array}$

Degrees of freedom:

The sample size is $n=10$

The degrees of freedom is,

$\begin{array}{c}d.f=n-2\\ =10-2\\ =8\end{array}$

From Table A.5 of the t-distribution in Appendix A, the critical value corresponding to the right tail area 0.025 and 8 degrees of freedom is 2.306.

Thus, the critical value is $\left(t_{{}_{\frac{\alpha }{2}}}\right)=2.306$.

The 95% confidence interval is,

$\begin{array}{c}C.I={\widehat{\mu }}_{\widehat{y}}-t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\le {\mu }_y\le {\widehat{\mu }}_{\widehat{y}}+t_{\left(\frac{\alpha }{2},n-2\right)}s\sqrt{\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =\left(30.6\pm 2.306\times 10.5350\sqrt{\frac{1}{10}+\frac{{\left(200-125.1\right)}^2}{42,864.9}}\right)\\ =\left(30.6\pm 8.227558\right)\\ =\left(22.37244,38.82756\right)\end{array}$

Thus, the 95% specified confidence interval for the true mean %total suspended solids removed when the amount filtered is 100,000 liters is $\underset{\_}{\left(22.37244,38.82756\right)}$.

Interpretation:

There is 95% confident that, the true mean %total suspended solids removed when the amount filtered is 100,000 liters lies between 22.37244 and 38.82756.

Comparison:

For 100,000 amount filtered, the value of x is $x=100$ and for 200,000 amount filtered, the value of x is $x=200$.

The mean amount filtered is $\underset{\_}{\overline{x}=125.1}$.

Here, the observation $x^{*}=100$ is close to mean value $\overline{x}=125.1$ than the observation $x^{*}=200$.

The general formula to obtain $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}}=s\times \sqrt{\frac{1}{n}+\frac{{\left(x^{*}-\overline{x}\right)}^2}{S_{xx}}}$.

For $x^{*}=100$ the value of $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}\left(100\right)}=s\times \sqrt{\frac{1}{10}+\frac{{\left(100-125.1\right)}^2}{42,864.9}}$.

For $x^{*}=200$ the value of $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}\left(200\right)}=s\times \sqrt{\frac{1}{10}+\frac{{\left(200-125.1\right)}^2}{42,864.9}}$.

In the two quantities, the only difference is the values ${\left(200-125.1\right)}^2$ and ${\left(100-125.1\right)}^2$.

In general, the value of the quantity ${\left(200-125.1\right)}^2$ will be larger than the value of ${\left(100-125.1\right)}^2$. Since, $x^{*}=100$ is close to $\overline{x}=125.1$ than $x^{*}=200$.

Therefore, the value $s_{\widehat{Y}\left(200\right)}$ will be larger than the value of $s_{\widehat{Y}\left(100\right)}$.

The confidence interval will be wider for large value of $s_{\widehat{Y}}$.

Here, $s_{\widehat{Y}}$ is higher for $x^{*}=200$.

Thus, the confidence interval is wider for $x^{*}=200$.

g.

To determine

Find the 95% prediction interval for the single value of %total suspended solids removed when the amount filtered is 100,000 liters.

Compare the width of the prediction intervals for 100,000 liters and 200,000 liters amount filtered.

Answer to Problem 48E

The 95% prediction interval for the single value of %total suspended solids removed when the amount filtered is 100,000 liters is $\underset{\_}{\left(4.950886,56.24911\right)}$.

The prediction interval for 100,000 liters of amount filtered will be narrower than the interval for 200,000 liters of amount filtered.

Explanation of Solution

Calculation:

From the MINITAB output obtained in part (b), the regression line for the variables %total suspended solids removed $\left(y\right)$ and amount filtered $\left(x\right)$  is $\underset{\_}{\stackrel{⌢}{y}=52.6-0.220x}$.

From part (c), the expected value of %total suspended solids removed with $x=100$ is 30.6.

Prediction interval for a single future value:

Prediction interval is used to predict a single value of the focus variable that is to be observed at some future time. In other words it can be said that the prediction interval gives a single future value rather than estimating the mean value of the variable.

The general formula for $\left(1-\alpha \right)$% prediction interval for the conditional mean at $x=x_p$ is,

$P.I={\widehat{y}}_p\pm t_{\frac{\alpha }{2}}s\sqrt{1+\frac{1}{n}+\frac{{\left(x_p-{\displaystyle \sum _i\frac{x_i}{n}}\right)}^2}{S_{\text{xx}}}}$

where ${\widehat{y}}_p$ be the predicted value of the response variable at $x=x_p$ and $S_{\text{xx}}={\displaystyle \sum _i{x}_i^2}-\frac{{\left({\displaystyle \sum _i{x}_i}\right)}^2}{n}$

From the MINITAB output in part (b), the value of the standard error of the estimate is $s=10.5350$.

From part (c), the mean chlorine flow is $\underset{\_}{\overline{x}=125.1}$ and the covariance term is $S_{\text{xx}}=42,864.9$.

Critical value:

For 95% confidence level,

$\begin{array}{c}1-\alpha =1-0.95\\ \alpha =0.05\\ \frac{\alpha }{2}=\frac{0.05}{2}\\ =0.025\end{array}$

Degrees of freedom:

The sample size is $n=10$

The degrees of freedom is,

$\begin{array}{c}d.f=n-2\\ =10-2\\ =8\end{array}$

From Table A.5 of the t-distribution in Appendix A, the critical value corresponding to the right tail area 0.025 and 8 degrees of freedom is 2.306.

Thus, the critical value is $\left(t_{{}_{\frac{\alpha }{2}}}\right)=2.306$.

The 95% prediction interval is,

$\begin{array}{l}P.I={\widehat{y}}_p\pm t_{\frac{\alpha }{2}}s\sqrt{1+\frac{1}{n}+\frac{{\left(x_p-\overline{x}\right)}^2}{S_{\text{xx}}}}\\ =30.6\pm \left(2.306\right)\left(10.5350\right)\sqrt{1+\frac{1}{10}+\frac{{\left(100-125.1\right)}^2}{42,864.9}}\\ =30.6\pm 25.64911\\ =\left(4.950886,56.24911\right)\end{array}$

Thus, the 95% prediction interval for the single value of %total suspended solids removed when the amount filtered is 100,000 liters is $\underset{\_}{\left(4.950886,56.24911\right)}$.

Interpretation:

For repeated samples, there is 95% confident that the single value of % total suspended solids removed when the amount filtered is 100,000 liters will lie between 4.950886 and 56.24911.

Comparison:

For 100,000 amount filtered, the value of x is $x=100$ and for 200,000 amount filtered, the value of x is $x=200$.

The mean amount filtered is $\underset{\_}{\overline{x}=125.1}$.

Here, the observation $x^{*}=100$ is close to mean value $\overline{x}=125.1$ than the observation $x^{*}=200$.

The general formula to obtain $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}}=s\times \sqrt{\frac{1}{n}+\frac{{\left(x^{*}-\overline{x}\right)}^2}{S_{xx}}}$.

For $x^{*}=100$ the value of $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}\left(100\right)}=s\times \sqrt{\frac{1}{10}+\frac{{\left(100-125.1\right)}^2}{42,864.9}}$.

For $x^{*}=200$ the value of $s_{\widehat{Y}}$ is,

$s_{\widehat{Y}\left(200\right)}=s\times \sqrt{\frac{1}{10}+\frac{{\left(200-125.1\right)}^2}{42,864.9}}$.

In the two quantities, the only difference is the values ${\left(200-125.1\right)}^2$ and ${\left(100-125.1\right)}^2$.

In general, the value of the quantity ${\left(200-125.1\right)}^2$ will be larger than the value of ${\left(100-125.1\right)}^2$. Since, $x^{*}=100$ is close to $\overline{x}=125.1$ than $x^{*}=200$.

Therefore, the value $s_{\widehat{Y}\left(200\right)}$ will be larger than the value of $s_{\widehat{Y}\left(100\right)}$.

The prediction interval will be wider for large value of $s_{\widehat{Y}}$.

Here, $s_{\widehat{Y}}$ is higher for $x^{*}=200$.

Thus, the prediction interval is wider for $x^{*}=200$.