
Concept explainers
(a)
Draw the influence lines for the reactions
Determine the reactions at B, C, D and E, moments at C and D.
(a)
Explanation of Solution
Given Information:
The uniform load (w) is 2 kips/ft.
Calculation:
Influence line for reaction at
Consider the portion AF
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 1.
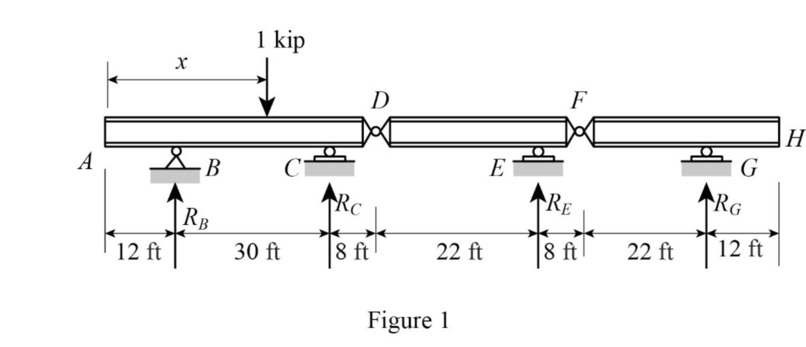
Refer Figure 1.
Find the equation support reaction
Take moment about point F from H.
Consider clockwise moment as negative and anticlockwise moment as positive
Consider the portion FH
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 2.
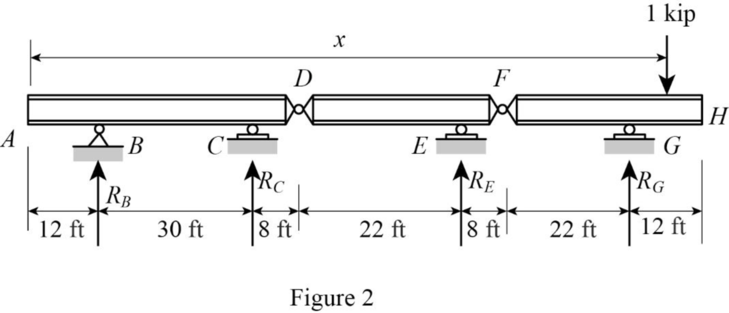
Refer Figure 2.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation support reaction
Take moment about point F from H.
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | 0 |
| 12 | 0 | |
| C | 42 | 0 |
| D | 50 | 0 |
| E | 72 | 0 |
| F | 80 | 0 |
| G | 102 | 1 |
| H | 114 | 1.55 |
Draw the influence lines for
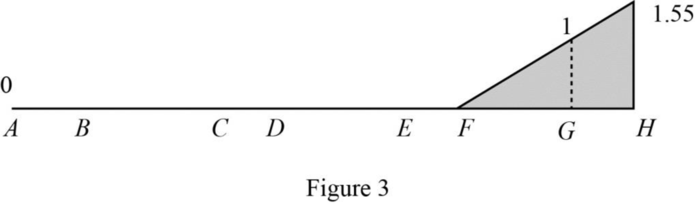
Refer Figure 3.
Determine the reaction at G.
Therefore, the reaction at G is
Influence line for reaction
Consider the portion AD
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 4.
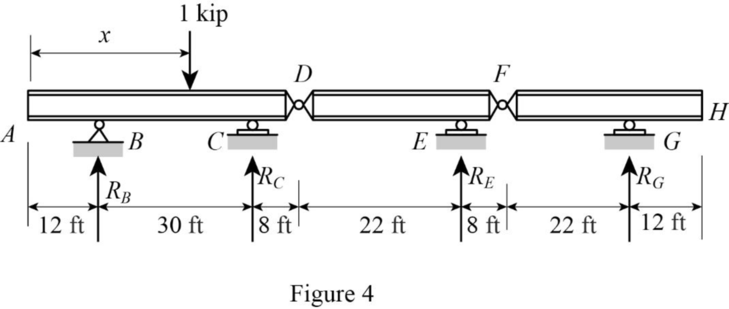
Refer Figure 4.
Find the equation support reaction
Take moment about point D from H.
Consider clockwise moment as negative and anticlockwise moment as positive
Consider the portion DF
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 5.
Refer Figure 5.
Find the equation support reaction
Take moment about point F from H.
Consider the portion FH
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 6.
Refer Figure 6.
Find the equation support reaction
Take moment about point F from H.
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | 0 |
| 12 | 0 | |
| C | 42 | 0 |
| D | 50 | 0 |
| E | 72 | 1 |
| F | 80 | 1.364 |
| G | 102 | 0 |
| H | 114 | ‑0.744 |
Draw the influence lines for
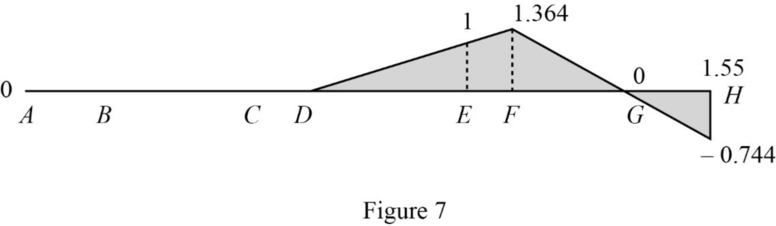
Refer Figure 7.
Determine the reaction at E.
Therefore, the reaction at E is
Influence line for reaction
Consider the portion AD
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 8.
Refer Figure 8.
Find the equation support reaction
Take moment about point B from H.
Consider the portion DF
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 9.
Refer Figure 9.
Find the equation support reaction
Take moment about point B from H.
Consider the portion FH
Apply a 1 kip unit moving load at a distance of
Sketch the free body diagram of beam as shown in Figure 10.
Refer Figure 6.
Find the equation support reaction
Take moment about point B from H.
Consider clockwise moment as negative and anticlockwise moment as positive
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | ‑0.4 |
| 12 | 0 | |
| C | 42 | 1 |
| D | 50 | 1.27 |
| E | 72 | 0 |
| F | 80 | ‑0.46 |
| G | 102 | 0 |
| H | 114 | 0.25 |
Draw the influence lines for
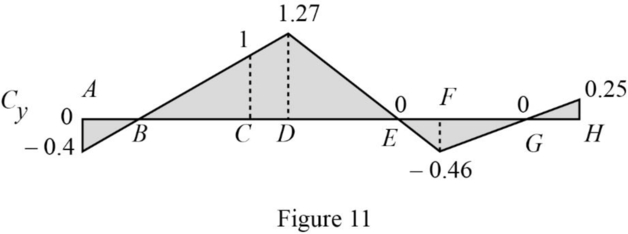
Refer Figure 11.
Determine the reaction at C.
Therefore, the reaction at C is
Influence line for reaction
Consider the portion AD
Refer Figure 8.
Consider upward force as positive and anticlockwise moment as negative.
Find the equation support reaction
Consider vertical equilibrium equation.
Consider the portion DF
Refer Figure 9.
Find the equation support reaction
Consider vertical equilibrium equation.
Consider the portion FH
Refer Figure 6.
Find the equation support reaction
Consider vertical equilibrium equation.
Consider upward force as positive and anticlockwise moment as negative.
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | 1.4 |
| 12 | 1 | |
| C | 42 | 0 |
| D | 50 | ‑0.25 |
| E | 72 | 0 |
| F | 80 | 0.1 |
| G | 102 | 0 |
| H | 114 | 0.063 |
Draw the influence lines for
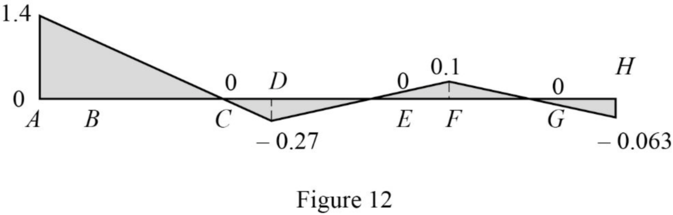
Refer Figure 12.
Determine the reaction at B.
Therefore, the reaction at B is
Influence line for the moment at section C:
Consider portion AC
Find the equation of moment at C for portion AC.
Apply a 1 kip in the portion AC from A.
Sketch the free body diagram of the section CH as shown in Figure 13.
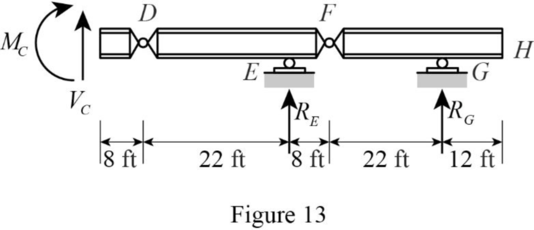
Find the equation of moment at C of portion AC.
Consider portion CD
Find the equation of moment at C for portion CD.
Apply a 1 kip in the portion CD from A.
Sketch the free body diagram of the section AC as shown in Figure 14.
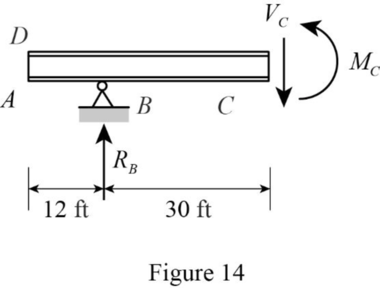
Find the equation of moment at C of portion CD.
Consider portion DF
Find the equation of moment at C for portion DF.
Apply a 1 kip in the portion DF from A.
Sketch the free body diagram of the section AC as shown in Figure 15.
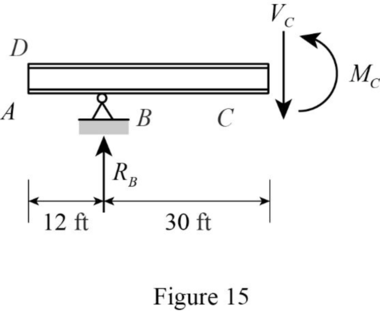
Find the equation of moment at C of portion DF.
Consider portion FH
Find the equation of moment at C for portion FH.
Apply a 1 kip in the portion FH from A.
Sketch the free body diagram of the section AC as shown in Figure 16.
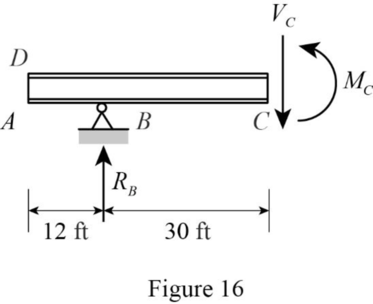
Find the equation of moment at C of portion FH.
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | 0 |
| 12 | 0 | |
| C | 42 | 0 |
| D | 50 | ‑8 |
| E | 72 | 0 |
| F | 80 | +2.73 |
| G | 102 | 0 |
| H | 114 | ‑1.89 |
Draw the influence lines for
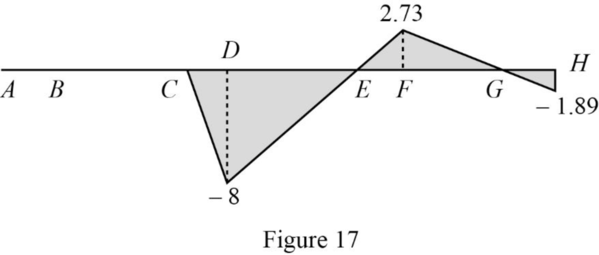
Refer Figure 17.
Determine the moment at C.
Therefore, the moment at C is
Influence line for the moment at section E:
Consider portion AE
Find the equation of moment at D for portion AE.
Apply a 1 kip in the portion AE from A.
Sketch the free body diagram of the section EH as shown in Figure 18.
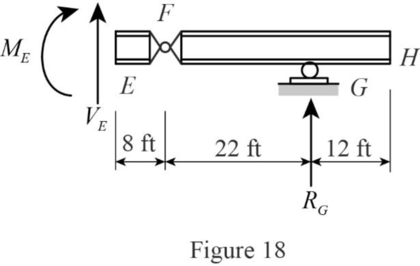
Find the equation of moment at E of portion AE.
Consider portion EF
Find the equation of moment at E for portion EF.
Apply a 1 kip in the portion DF from A.
Sketch the free body diagram of the section AC as shown in Figure 19.
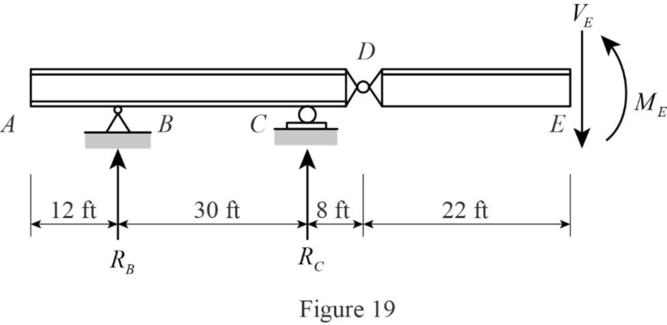
Find the equation of moment at E of portion EF.
Consider portion FH
Find the equation of moment at E for portion FH.
Apply a 1 kip in the portion FH from A.
Sketch the free body diagram of the section AC as shown in Figure 20.
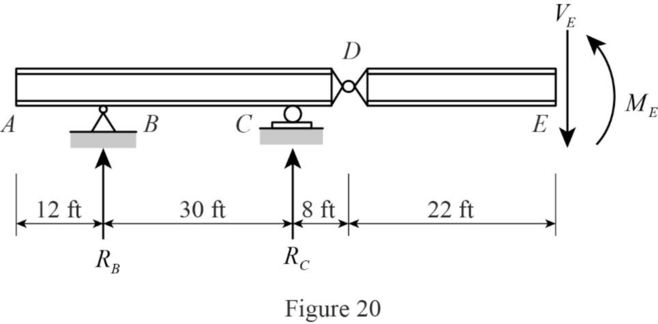
Find the equation of moment at D of portion FH.
Thus, the equations of the influence line for
Find the value of influence line ordinate of
| Points | x | |
| A | 0 | 0 |
| 12 | 0 | |
| C | 42 | 0 |
| D | 50 | 0 |
| E | 72 | 0 |
| F | 80 | ‑8 |
| G | 102 | 0 |
| H | 114 | 4.04 |
Draw the influence lines for
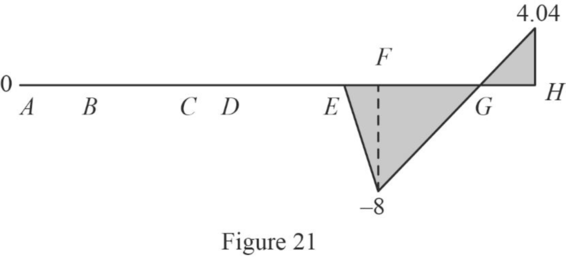
Refer Figure 21.
Determine the moment at E.
Therefore, the moment at E is
Want to see more full solutions like this?
Chapter 12 Solutions
UCD FUND OF STRUCTURAL ANALYSIS 5E
- Can you please do hand calcs and breakdown each steparrow_forwardQ4. Statically determinate or indeterminate frame analysis by the stiffness method a) Determine the stiffness matrix of the frame as shown in Fig. 4. Nodes 1 and 3 are fixed supports. Assume I = 300(10%) mm, A = 10(103) mm², E = 200 GPa for each member. Indicate the degrees-of freedom in all the stiffness matrices. Use the values of L3-3.5 m, w = 24 kN/m and P = 30 kN. Note, L4-1.8L3 (i.e. 1.8 times L3). b) Determine all the displacement components at node 2 and all internal reactions at node 2. Show all calculations. c) Draw the BMD of the frame on the compression side showing all the salient values. Show all calculations. d) Repeat the problem using the Strand 7. Show the model with all the nodes and element numbers and boundary conditions. Submit a hard copy from Strand7 showing all the reactions (highlight these in the hard copy). Display the bending moment diagram for the frame. 4 e) Compare the BMD from Strand 7 with the theoretical one and compare the respective values of…arrow_forwardCan you please break down all the hand calcs and make sure we answer the below. a Determine the global stiffness matrices (k’) of all truss members including correct degrees-of freedom (dof)-3x3 b Determine the global stiffness matrix (K) of the whole truss (include dof numbers) c i) Calculate vectors D and Q (4+4). ii) Show partition and solve KD=Q iii) Calculate all the member forces d i) Solve the problem using Strand7 (model) (You must model the beam property as truss) ii) Display of deflected shape, nodal displacements and member forces (3+3+3) e Comparison of member forces and comments , comparison of displacemnts and commnetsarrow_forward
- YOU HAVE A UNIFORM SUBGRADE ELEVATION FOR YOUR BUILDING FOUNDATION THAT HASBEEN VERIFIED. YOUR SLAB IS DESIGNED TO BE 12 INCHES THICK.USING THE GIVENDIMENSIONS AROUND THE PROPOSED BUILDING FOUNDATION, CALCULATE THE CUBIC FEETAND THE CUBIC YARDS OF CONCRETE NEEDED FOR THE FOUNDATION **Sketch Attached**arrow_forwardWHAT ARE THE COORDINATES (N,E) AT POINT A AND POINT B IN THE SKETCH (ATTACHED)arrow_forwardCan you please do with hand calcs and answer the following: a Determine the global stiffness matrix (K) of the beam including indicating correct degrees-of freedom (dof) b i) Calculate vectors D and Q ii) Show partition and solve KD=Q for D iii) Calculate all reactions c BMD & max BM, deflected shape d i) Solve the problem using Strand7 (model) ii) Display the deflected shape and BMD e Comparisons of reactions + Max BM including commentsarrow_forward
- 5-1. Determine the force in each member of the truss, and state if the members are in tension or compression.arrow_forwardI have the correct answer provided, just lookng for a more detailed breadown of how the answer was obtained thanks.arrow_forwardQ1. Statically indeterminate beam analysis. a) Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the moment distribution method. The beam is subjected to an UDL of w kN/m. L1= 0.4L. Assume the support at C is pinned, and A and B are roller supports. E = 200 GPa, I=250x106 mm². Use the values of w = 50 kN/m and L = 6 b) Draw the shear force and bending diagrams for the entire beam. c) Calculate the BMs at all the joints of the same beam shown in Fig.1 using the slope deflection method. d) Compare the values of BMs obtained using the two methods a) and c) and comment. w kN/m £1m Lm m Fig 1. Beam for Q1arrow_forward
- I have the answer provided for the question, just looking for a more detailed breadown of how it was obtained thanks.arrow_forwardQ5.--Finite-element-modelling. a) → Draw-a-2D-element-and-show-the dots (degrees of freedom). Draw-all-the-2D-elements. used-in-Strand 7..Explain the differences between-these-elements-in-terms-of-the-no..of. nodes-and-interpolation/shape-functions used. b)→A-8-m-x-8-m-plate (in-the-xx-plane)-with-8-mm-thickness, is fixed-at-all-the-edges.and.is. loaded-by-a-pressure-loading-of-4 kN/m2.-in-the-downward-(-2)-direction.-The-plate.is. made-of-steel-(E=-200 GPa, density-7850-kg/m3). Explain-the-steps-involved-in-setting. up-a-Strand 7-model-for-this-problem. Your-explanation-should-include-how-the-given. input-data-for-this-problem-will-be-used-in-Strand 7-modelling. Explain how you would. determine the maximum-deflection-from-the-Strand 7-output.-1 11arrow_forwardI need Help some hw for AutoCAD please use measure front top and side viewarrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





