Chapter 12, Problem 40P

(a)

To determine

Draw the influence lines for the horizontal and vertical reactions at support A and the member forces in members BC, CM, and ML.

Explanation of Solution

Influence line for the vertical reaction at A.

The influence line ordinate of $\left(A_y\right)$ are determined by applying a 1-kip load at successive panel points.

Apply 1 kip at D.

Find the vertical reaction at support A.

The reaction is determined by applying a 1-kip load at successive panel points.

Apply 1 kip load at C.

Draw the free body diagram as shown in Figure 1.

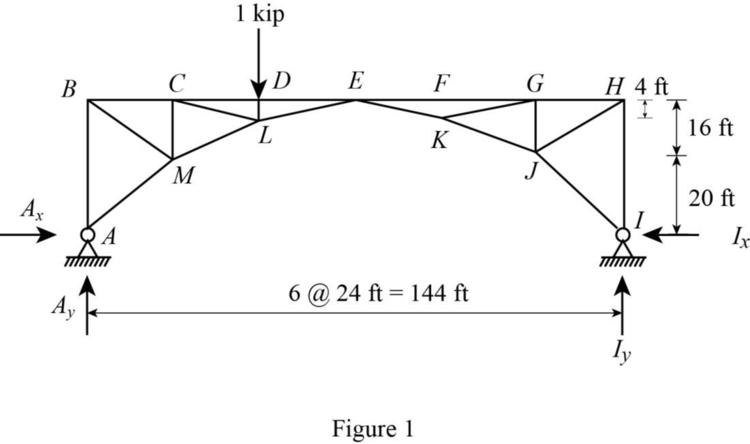
Refer Figure 1.

Consider moment equilibrium at I.

$\begin{array}{l}\Sigma M_I=0\\ A_y\left(144\right)=1\left(96\right)\\ A_y=0.667\text{k}\end{array}$

Thus, the influence line ordinate of vertical reaction at A is 0.667.

Similarly find the influence line ordinate of $A_y$ by applying 1 kip at A, B, D, E, F, G, and H and tabulate the values in Table 1.

Points	x (ft)	Influence line ordinate of $A_y$
B	0	1
C	24	0.833
D	48	0.667
E	72	0.5
F	96	0.333
G	120	0.167
H	144	0

Draw the influence line ordinate of $A_y$ using Table 1 as in Figure 2.

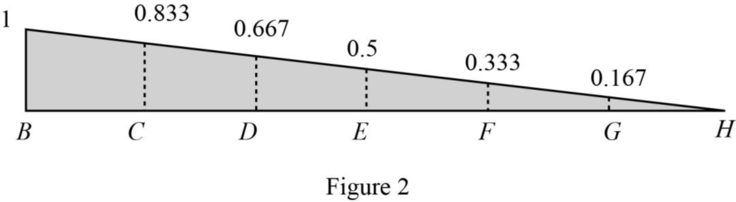
Influence line for the horizontal reaction  at A.

The influence line ordinate of $\left(A_x\right)$ are determined by applying a 1-kip load at successive panel points.

Apply 1 kip at D.

Find the horizontal reaction at support A.

The reaction is determined by applying a 1-kip load at successive panel points.

Apply 1 kip load at C.

Draw the free body diagram as shown in Figure 3.

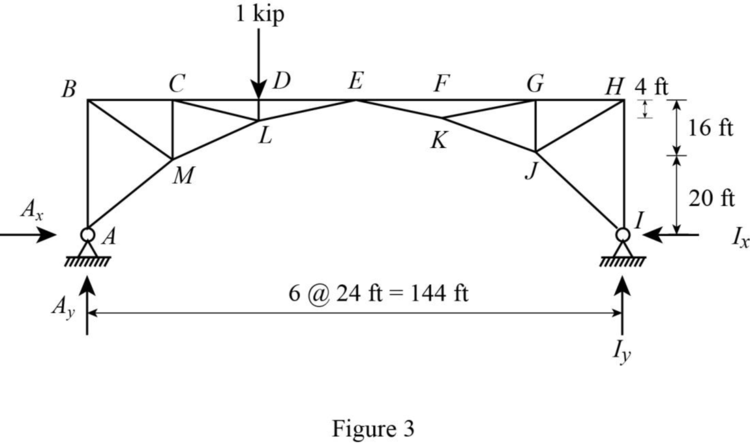
Refer Figure 4.

Consider moment equilibrium at E.

$\begin{array}{l}\Sigma M_I=0\\ A_y\left(72\right)-A_x\left(36\right)-1\left(24\right)=0\\ 0.667\left(72\right)-36A_x=24\\ 36A_x=24\\ A_x=0.667\text{k}\end{array}$

Thus, the influence line ordinate of horizontal reaction at A is 0.667.

Similarly find the influence line ordinate of $A_x$ by applying 1 kip at A, B, D, E, F, G, and H and tabulate the values in Table 2.

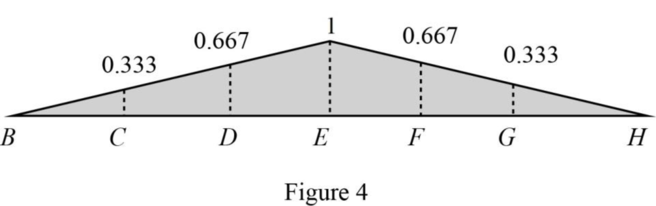
Points	x (ft)	Influence line ordinate of $A_x$
B	0	0
C	24	0.333
D	48	0.667
E	72	1
F	96	0.667
G	120	0.333
H	144	00

Draw the influence line ordinate of $A_x$ using Table 2 as in Figure 4.

Influence line for the force in member BC.

Find the force $\left(F_{BC}\right)$ in member BC.

The influence line ordinate of $F_{BC}$ are determined by applying a 1-kip load at successive panel points.

Apply 1 kip at C and consider a section passes through members BC, CM, and ML.

Sketch the free body diagram of the section as in Figure 5.

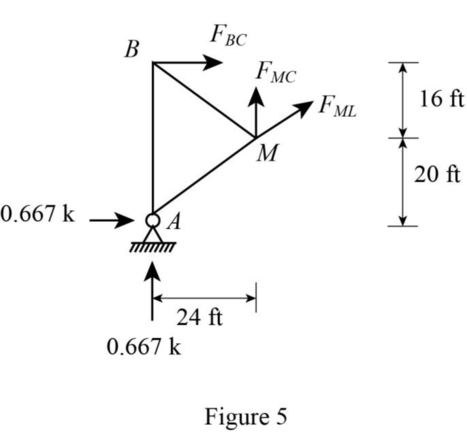
Refer Figure 5.

Find the member force BC.

Consider moment equilibrium at M.

$\begin{array}{l}\Sigma M_M=0\\ 0.667\left(20\right)-0.667\left(24\right)-F_{BC}\left(16\right)=0\\ F_{BC}=-0.167\text{k}\end{array}$

Thus, the influence line ordinate of member force BC at D is ‑0.167.

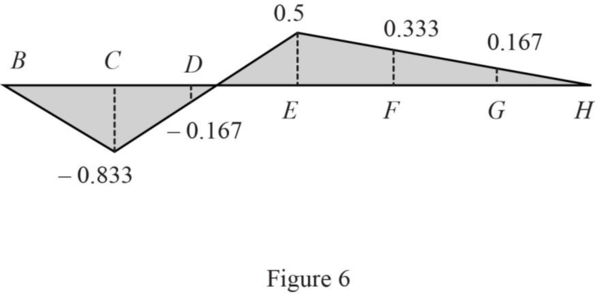
Similarly find the influence line ordinate of $F_{BC}$ by applying 1 kip at B, C, D, E, F, G, and H and tabulate the values in Table 4.

Points	x (ft)	Influence line ordinate of $F_{BC}$
B	0	0
C	24	‑0.833
D	48	‑0.167
E	72	0.5
F	96	0.333
G	120	0.167
H	144	0

Draw the influence line ordinate of $F_{BC}$ using Table 4 as in Figure 6.

Influence line for the force in member ML.

Find the force $\left(F_{ML}\right)$ in member ML.

The influence line ordinate of $F_{ML}$ are determined by applying a 1-kip load at successive panel points.

Apply 1 kip at C and consider a section passes through members BC, CM, and ML.

Sketch the free body diagram of the section as in Figure 7.

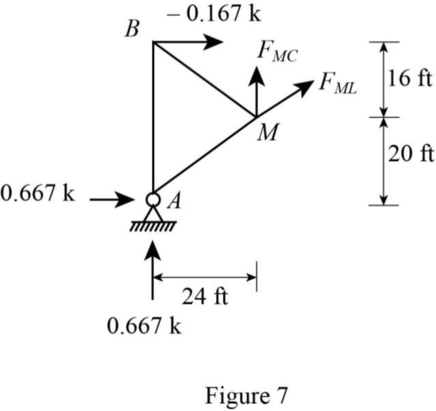
Refer Figure 7.

The slope of member ML is 24 ft horizontal and 12 ft vertical.

Find the member force ML.

Consider horizontal equilibrium equation.

$\begin{array}{l}\Sigma F_x=0\\ 0.667+\left(-0.167\right)+F_{ML}\left(\frac{24}{\sqrt{{24}^2+{12}^2}}\right)=0\\ 0.894F_{ML}=-0.5\\ F_{ML}=-0.56\text{kips}\end{array}$

Thus, the influence line ordinate of member force ML at D is ‑0.56.

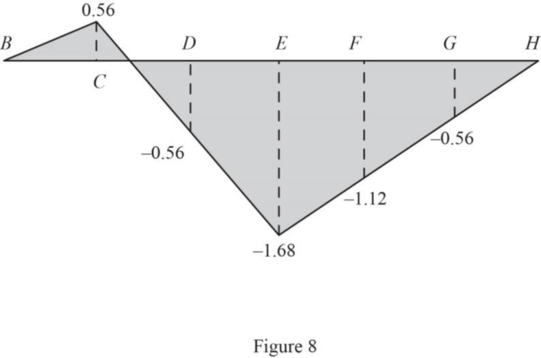
Similarly find the influence line ordinate of $F_{ML}$ by applying 1 kip at B, C, D, E, F, G, and H and tabulate the values in Table 5.

Points	x (ft)	Influence line ordinate of $F_{ML}$
B	0	0
C	24	0.56
D	48	‑0.56
E	72	‑1.68
F	96	‑1.12
G	120	‑0.56
H	144	0

Draw the influence line ordinate of $F_{ML}$ using Table 5 as in Figure 8.

Influence line for the force in member CM.

Find the force $\left(F_{CM}\right)$ in member CM.

The influence line ordinate of $F_{CM}$ are determined by applying a 1-kip load at successive panel points.

Apply 1 kip at C and consider a section passes through members BC, CM, and ML.

Sketch the free body diagram of the section as in Figure 9.

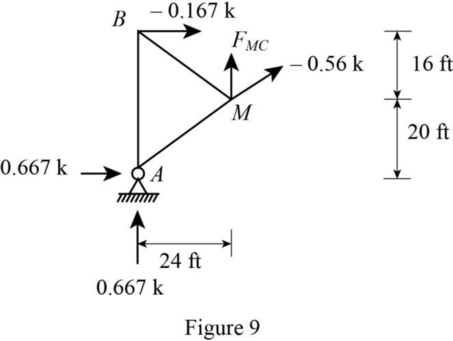
Refer Figure 9.

The slope of member ML is 24 ft horizontal and 12 ft vertical.

Find the member force CM.

Consider vertical equilibrium equation.

$\begin{array}{l}\Sigma F_y=0\\ 0.667+F_{MC}+F_{ML}\left(\frac{12}{\sqrt{{24}^2+{12}^2}}\right)=0\\ 0.667+F_{MC}+\left(-0.56\right)\left(\frac{12}{\sqrt{{24}^2+{12}^2}}\right)=0\\ 0.667+F_{CM}+\left(-0.56\right)\left(0.447\right)=0\\ F_{CM}=-0.416\text{k}\end{array}$

Thus, the influence line ordinate of member force CM at D is ‑0.416.

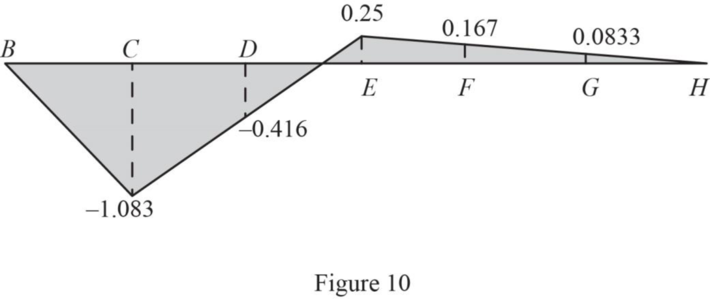
Similarly find the influence line ordinate of $F_{CM}$ by applying 1 kip at B, C, D, E, F, G, and H and tabulate the values in Table 5.

Points	x (ft)	Influence line ordinate of $F_{CM}$
B	0	0
C	24	‑1.083
D	48	‑0.416
E	72	0.25
F	96	0.167
G	120	0.083
H	144	0

Draw the influence line ordinate of $F_{CM}$ using Table 5 as in Figure 10.

(b)

To determine

Find the forces (compression and tension) in bars CM and ML produced by the dead load.

Answer to Problem 40P

The dead load force in member CM is $\underset{\_}{115.1\text{k}\left(\text{C}\right)}$

The dead load force in member ML is $\underset{\_}{387.07\text{k}\left(\text{C}\right)}$

Explanation of Solution

Given Information:

The uniform dead load, $w_D$ is 4.8 kip/ft.

Calculation:

Refer Figure 11.

Sketch the influence line diagram of member CM as in Figure 11.

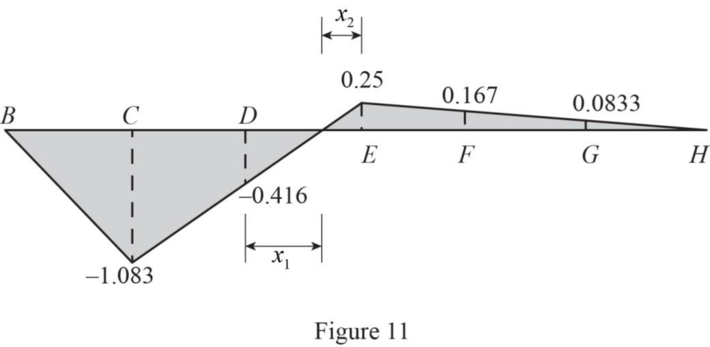
Refer Figure 11.

Find the length $x_1$ using similar triangle.

$\begin{array}{l}\frac{x_1}{0.416}=\frac{x_1+L_{CD}}{1.083}\\ 1.083x_1=0.416x_1+0.416L_{CD}\\ 1.083x_1-0.416x_1=0.416\left(24\right)\\ x_1=15\text{ft}\end{array}$

Find the length $x_2$ using similar triangle.

$\begin{array}{l}\frac{x_2}{0.25}=\frac{x_1}{0.416}\\ x_2=\frac{15}{0.416}\left(0.25\right)\\ x_2=9\text{ft}\end{array}$

Refer Figure 11.

Find the dead load force in member CM using the equation.

$\begin{array}{c}{F}_{CM}=w_D\left(\text{Area}\text{of}\text{influence line diagram}\right)\\ =w_D\left[\frac{1}{2}\left(-1.083\right)\left(L_{BD}+x_1\right)+\frac{1}{2}\left(0.25\right)\left(x_2+L_{EH}\right)\right]\\ =4.8\left[0.5\left(-1.083\right)\left(48+15\right)+0.5\left(0.25\right)\left(9+72\right)\right]\\ =4.8\left(-34.112+10.125\right)\\ =-115.1\text{k}\\ \text{=115}\text{.1}\text{k}\left(\text{Compresion}\right)\end{array}$

Therefore, the dead load force in member CM is $\underset{\_}{115.1\text{k}\left(\text{C}\right)}$

Refer Figure 9.

Sketch the influence line diagram of member ML as in Figure 12.

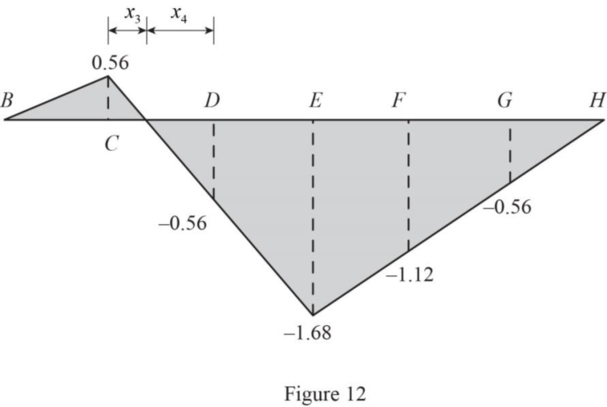
Refer Figure 12.

Find the length $x_3$ and $x_4$ using similar triangle.

$\begin{array}{l}\frac{x_4}{0.56}=\frac{x_4+L_{DE}}{1.68}\\ \frac{x_4}{0.56}=\frac{x_4+24}{1.68}\\ 1.68x_4=0.56x_4+13.44\\ x_4=12\text{ft}\end{array}$

Find the length $x_3$ and $x_4$ using similar triangle.

$\begin{array}{l}\frac{x_3}{0.56}=\frac{x_4+L_{DE}}{1.68}\\ 1.68x_3=0.56\left(x_4\right)+0.56L_{DE}\\ 1.68x_3=0.56\left(12\right)+0.56\left(24\right)\\ x_3=12\text{ft}\end{array}$

Refer Figure 11.

Find the dead load force in member CM using the equation.

$\begin{array}{c}{F}_{ML}=w_D\left(\text{Area}\text{of}\text{influence line diagram}\right)\\ =w_D\left[\frac{1}{2}\left(0.56\right)\left(L_{BC}+x_3\right)+\frac{1}{2}\left(-1.68\right)\left(x_4+L_{DH}\right)\right]\\ =4.8\left[0.5\left(0.56\right)\left(24+12\right)+0.5\left(-1.68\right)\left(12+96\right)\right]\\ =4.8\left(10.08-90.72\right)\\ =-387.07\text{k}\\ \text{=387}\text{.07}\text{k}\left(\text{Compresion}\right)\end{array}$

Therefore, the dead load force in member ML is $\underset{\_}{387.07\text{k}\left(\text{C}\right)}$

(c)

To determine

Find the forces (compression and tension) in bars CM due to live load.

Answer to Problem 40P

The maximum compression force in member CM due to live load is $\underset{\_}{-48.95\text{k}}$.

The maximum tension force in member CM due to live load is $\underset{\_}{13.1\text{k}}$

Explanation of Solution

Given Information:

The uniform live load, $w_L$ is 0.8 kip/ft.

The concentrated live load, P is 20 k.

Calculation:

Refer Figure 11.

Sketch the influence line diagram of member CM as in Figure 13.

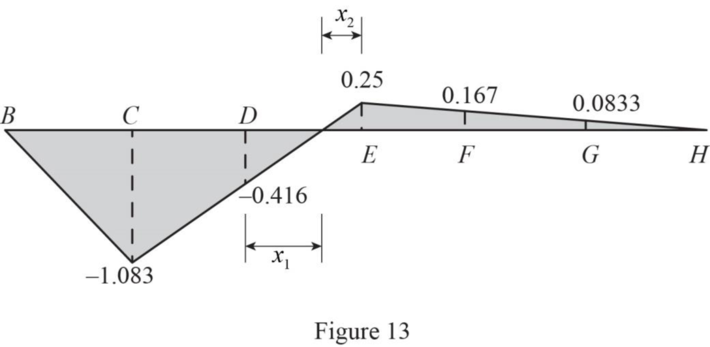
Refer Figure 13.

Find the maximum compression force in member CM using the equation.

$\begin{array}{c}{F}_{CM}=w_L\left(\text{negative area}\text{of}\text{influence line diagram}\right)+P\left(\text{maximum}\text{negative}\text{ordinate}\right)\\ =0.8\left[\frac{1}{2}\left(-1.083\right)\left(L_{BD}+x_1\right)\right]+20\left(-1.083\right)\\ =0.8\left[0.5\left(-1.083\right)\left(48+15\right)\right]+21.66\\ =-48.95\text{k}\end{array}$

Therefore, the maximum compression force in member CM due to live load is $\underset{\_}{-48.95\text{k}}$.

Find the maximum tension force in member CM using the equation.

$\begin{array}{c}{F}_{CM}=w_L\left(\text{positive area}\text{of}\text{influence line diagram}\right)+P\left(\text{maximum}\text{positive}\text{ordinate}\right)\\ =0.8\left[\frac{1}{2}\left(0.25\right)\left(L_{EH}+x_2\right)\right]+20\left(0.25\right)\\ =0.8\left[0.5\left(0.25\right)\left(72+9\right)\right]+5\\ =13.1\text{k}\end{array}$

Therefore, the maximum tension force in member CM due to live load is $\underset{\_}{13.1\text{k}}$.