
Concept explainers
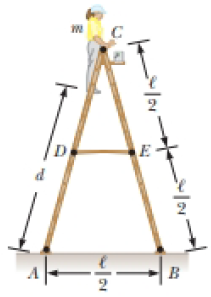
A stepladder of negligible weight is constructed as shown in Figure P12.40, with AC = BC = ℓ = 4.00 m. A painter of mass m = 70.0 kg stands on the ladder d = 3.00 m from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately.
Figure P12.40 Problems 40 and 41.
(a)
The tension in the horizontal bar
Answer to Problem 12.56AP
The tension in the horizontal bar
Explanation of Solution
The length of the each ladder is
The following figure shows the force diagram of the ladder

Figure-(I)
Formula to calculate the angle made by the ladder with horizontal is,
Here,
Substitute
Formula to calculate the torque about the point
Here,
Substitute
Formula to calculate the net torque about the point
Here,
Substitute
Substitute
Conclusion:
Therefore, the tension in the horizontal bar
(b)
The normal force at
Answer to Problem 12.56AP
The normal force at
Explanation of Solution
Formula to calculate the net torque about the point
Here,
Substitute
Substitute
Conclusion:
Therefore, the normal force at
(c)
The components of the force acting on the hinge point
Answer to Problem 12.56AP
The horizontal component of the force at hinge point
Explanation of Solution
Formula to calculate the net horizontal forces acting on the right half of the ladder is,
Here,
Substitute
Formula to calculate the net vertical forces acting on the right half of the ladder is,
Here,
Substitute
Conclusion:
Therefore, the vertical component of the force acting on the hinge point in right half of the ladder is
Want to see more full solutions like this?
Chapter 12 Solutions
Physics for Scientists and Engineers, Volume 1, Chapters 1-22
- A stepladder of negligible weight is constructed as shown in Figure P10.73, with AC = BC = = 4.00 m. A painter of mass m = 70.0 kg stands on the ladder d = 3.00 m from the bottom. Assuming the floor is frictionless, find (a) the tension in the horizontal bar DE connecting the two halves of the ladder, (b) the normal forces at A and B, and (c) the components of the reaction force at the single hinge C that the left half of the ladder exerts on the right half. Suggestion: Treat the ladder as a single object, but also treat each half of the ladder separately.arrow_forwardA uniform beam resting on two pivots has a length L = 6.00 m and mass M = 90.0 kg. The pivot under the left end exerts a normal force n1 on the beam, and the second pivot located a distance = 4.00 m from the left end exerts a normal force n2. A woman of mass m = 55.0 kg steps onto the left end of the beam and begins walking to the right as in Figure P10.28. The goal is to find the womans position when the beam begins to tip. (a) What is the appropriate analysis model for the beam before it begins to tip? (b) Sketch a force diagram for the beam, labeling the gravitational and normal forces acting on the beam and placing the woman a distance x to the right of the first pivot, which is the origin. (c) Where is the woman when the normal force n1 is the greatest? (d) What is n1 when the beam is about to tip? (e) Use Equation 10.27 to find the value of n2 when the beam is about to tip. (f) Using the result of part (d) and Equation 10.28, with torques computed around the second pivot, find the womans position x when the beam is about to tip. (g) Check the answer to part (e) by computing torques around the first pivot point. Figure P10.28arrow_forwardWhy is the following situation impossible? A worker in a factory pulls a cabinet across the floor using a rope as shown in Figure P12.36a. The rope make an angle = 37.0 with the floor and is tied h1 = 10.0 cm from the bottom of the cabinet. The uniform rectangular cabinet has height = 100 cm and width w = 60.0 cm, and it weighs 400 N. The cabinet slides with constant speed when a force F = 300 N is applied through the rope. The worker tires of walking backward. He fastens the rope to a point on the cabinet h2 = 65.0 cm off the floor and lays the rope over his shoulder so that he can walk forward and pull as shown in Figure P12.36b. In this way, the rope again makes an angle of = 37.0 with the horizontal and again has a tension of 300 N. Using this technique, the worker is able to slide the cabinet over a long distance on the floor without tiring. Figure P12.36 Problems 36 and 44.arrow_forward
- A construction worker of mass m, = 69.6 kg stands on a uniform ladder a distance d = 0.9 m from the bottom, measured along the ladder (Refer to the figure below). The ladder with mass m2 = 10.1 kg and length L = 3.8 m rests against a smooth wall. It makes an angle 31.3 degrees with the ground. There is a frictional force of magnitude f between the floor and the ladder. N, is the magnitude of the normal force exerted by the wall on the ladder, and N2 is the magnitude of the normal force exerted by the ground on the ladder. Take counterclockwise torques to be positive. What is the minimum coefficient of static friction required between the ladder and the ground so that the ladder does not slip? Give your answer to 2 decimal places. marrow_forwardA uniform beam of mass M = 10.0 kg and length L = 2.00 m is suspended from a ceiling at an angle of 30° below the horizontal. The beam is attached to the ceiling by a hinge at one end and a light support rope attached to the other end. What is the magnitude of the force by the hinge? 30° L= 2.0 m M= 10.0 kgarrow_forwardA uniform ladder stands on a rough floor and rests against a frictionless wall as shown in the figure. N2 mg d b Since the floor is rough, it exerts both a normal force N, and a frictional force f, on the ladder. However, since the wall is frictionless, it exerts only a normal force N, on the ladder. The ladder has a length of L = 4.70 m, a weight of W = 68.0 N, and rests against the wall a distance d = 3.75 m above the floor. If a person with a mass of m = 90 kg is standing on the ladder, determine the following. (a) the forces exerted on the ladder when the person is halfway up the ladder (Enter the magnitude only.) N1 N2 = f1 %3D (b) the forces exerted on the ladder when the person is three-fourths of the way up the ladder (Enter the magnitude only.) N1 = N N2 = f1arrow_forward
- A horizontal L=1.0 m long mb=12 kg uniform bar is hinged on the left end and pulled at the right end by a cable. The cable makes 24° angle with horizontal. A 20 kg store sign is suspended below the bar at d=0.18 m from the right end. Find the magnitude of horizontal hinge force.arrow_forwardIn the figure, a uniform beam of length 13.5 m is supported by a horizontal cable and a hinge at angle θ = 54.8°. The tension in the cable is 423 N. What are (a) the x-component and (b) the y-component of the gravitational force on the beam? What are (c) the x-component and (d) the y-component of the force on the beam from the hinge?arrow_forwardA 11.0-kg monkey climbs a uniform ladder with weight w = 1.40 × 102 N and length L = 2.60 m as shown in the figure below. The ladder rests against the wall and makes an angle of 0 = 60.0° with the ground. The upper and lower ends of the ladder rest on frictionless surfaces. The lower end is connected to the wall by a horizontal rope that is frayed and can support a maximum tension of only 80.0 N. Rope (a) Draw a force diagram for the ladder. Choose File no file selected This answer has not been graded yet. (b) Find the normal force exerted on the bottom of the ladder. (c) Find the tension in the rope when the monkey is two-thirds of the way up the ladder. N (d) Find the maximum distance d (along the ladder) that the monkey can climb up the ladder before the rope breaks. (e) If the horizontal surface were rough and the rope were removed, how would your analysis of the problem change? What other information would you need to answer parts (c) and (d)? This answer has not been graded yet.…arrow_forward
- Your answer is partially correct. The system in the figure is in equilibrium. A concrete block of mass 221 kg hangs from the end of the uniform strut of mass 45.1 kg. For angles = 39.4° and 0 = 55.7°, find (a) the tension T in the cable and the (b) horizontal and (c) vertical components of the force on the strut from the hinge. (a) Number i 98100 (b) Number i (c) Number i T Strut 0 -Hinge Units Units Units N <arrow_forwardThe figure shows a horizontal beam of mass M = 22 kg and length L = 3.9 m supported at its left end by a frictionless pin and at the other end by an ideal cable attached to wall h = 1.6 m above the beam. A mass m = 9.7 kg is suspended from the beam a distance d = 1.6 m from the wall. Find the magnitude R of the "reaction force" exerted by the pin on the beam. h R = -d- m M L Narrow_forwardA uniform ladder 6.9 m long weighing 430 N rests with one end on the ground and the other end against a perfectly smooth vertical wall. The ladder rises at 59.5 o above the horizontal floor. A 800 N painter finds that she can climb 2.65 m up the ladder, measured along its length, before it begins to slip. Normal force exerted on ladder = 1230N Part A: What force does the wall exert on the ladder? F=____N Part B: Find the friction force that the floor exerts on the ladder. F=____Narrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning



