
Concept explainers
Disk A rotates in a horizontal plane about a vertical axis at the
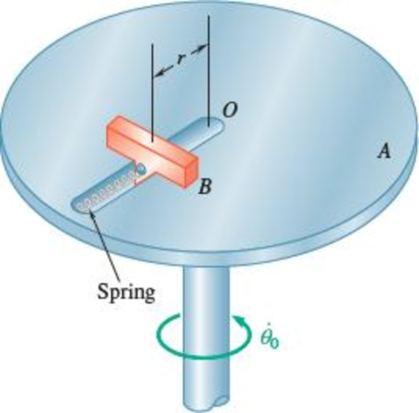
(a)
Find the position of the slider and horizontal force exerted on the slider by disk at
Answer to Problem 12.133RP
The position of the slider at
The horizontal force exerted on the slider by disk at
Explanation of Solution
Given information:
The polar coordinate
The mass
The distance
The spring constant (k) is 100 N/m.
Calculation:
Consider the Position of the slider is in point O
Find the displacement of spring when
Consider distance of the slider (r) from the point O is 500 mm.
Find the displacement of spring when
Substitute 500 mm for r.
Find the restoring force (F) of spring when
Substitute 100 N/m for k and 500 mm for
Sketch the free body diagram and kinetic diagram of forces on disk A and spring as shown in in Figure (1).
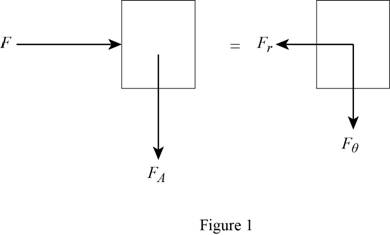
Refer Figure (1).
Write the equation of radial component of acceleration
Apply Newton’s law of equation along radial direction.
The radial force is equal to the restoring force.
Find the equation of restoring force (F).
Substitute
Substitute
Write the equation of
Integrate Equation (1) to find
Use Equation (1) to substitute for
Slider B is at initial position when
Write
Integrate Equation (4) to find
Use Equation (3) to substitute for
Find the position of the slider at
Use Equation (4) to substitute for
Thus, the position of the slider at
Refer Figure 1.
Apply Newton’s law of Equation along transverse direction.
Write the transverse component of acceleration
Here,
The transverse force is the horizontal force exerted on the slider by disk.
The disk is rotating at constant rate. Therefore, the polar coordinate of transverse acceleration,
Find the horizontal force exerted on the slider by disk at
Write the equation of transverse force
Substitute
Substitute 0 for
Substitute Equation (3) in Equation (7).
Thus, the horizontal force exerted on the slider by disk at
(b)
Find the position of the slider and horizontal force exerted on the slider by disk at
Answer to Problem 12.133RP
The position of the slider at
The horizontal force exerted on the slider by disk at
Explanation of Solution
Calculation:
Consider the Position of the slider is in point O
Find the displacement of spring when
Consider distance of the slider (r) from the point O is 500 mm.
Find the displacement of spring when
Substitute 500 mm for r.
Find the restoring force (F) of spring when
Substitute 200 N/m for k and 500 mm for
Refer Figure (1).
Write the equation of radial component of acceleration
Apply Newton’s law of equation along radial direction.
The radial force is equal to the restoring force.
Find the equation of restoring force (F).
Substitute
Substitute
Write the equation of radial velocity of the slider in terms of r.
Here,
Write equation of the rate of change of position coordinate in terms of differential equation.
Apply differentiation to Equation (8)
Rewrite Equation (10) by multiplying and dividing the right-hand side by dr.
Substitute Equation (10) to rewrite Equation (11).
Substitute Equation (8) to rewrite Equation (12).
Substitute
Apply the limits to integrate the Equation (14).
At the time of instant
Substitute Equation (8) in Equation (15).
Integrate Equation (16).
Use spherical polar coordinates and choose,
Differentiate Equation (18).
Rewrite Equation (18).
Rewrite Equation (20) for
Use Equation (20) and (21) to change the values of limit in Equation (17).
Apply the trigonometric formula of
Use Equation (23) to rewrite Equation (22).
Substitute 0.5m for
Thus, the position of the slider at
Find the radial polar coordinate of velocity using Equation (24).
Differentiate Equation (24) with respect to t.
Substitute 500 mm for
Find the horizontal force exerted on the slider by disk at
Substitute
Substitute 0.1 s for t and
Thus, the horizontal force exerted on the slider by disk at
Want to see more full solutions like this?
Chapter 12 Solutions
VECTOR MECH...,STAT.+DYNA.(LL)-W/ACCESS
Additional Engineering Textbook Solutions
Vector Mechanics For Engineers
BASIC BIOMECHANICS
Database Concepts (8th Edition)
Thermodynamics: An Engineering Approach
Mechanics of Materials (10th Edition)
Modern Database Management
- Note: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question: (In the image as provided)arrow_forwardNote: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question: The rectangular gate shown below is 3 m wide. Compute the force P needed to hold the gate in the position shown.arrow_forwardNote: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question1: If the following container is 0.6m high, 1.2m wide and half full with water, determine the pressure acting at points A, B, and C if ax=2.6ms^-2.arrow_forward
- Please read the imagearrow_forwardChapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scoresarrow_forwardConsider a large 6-cm-thick stainless steel plate (k = 15.1 W/m-K) in which heat is generated uniformly at a rate of 5 × 105 W/m³. Both sides of the plate are exposed to an environment at 30°C with a heat transfer coefficient of 60 W/m²K. Determine the value of the highest and lowest temperature. The highest temperature is The lowest temperature is °C. °C.arrow_forwardSketch and explain a PV Diagram and a Temperature Entropy Diagram for a 4 stroke diesel engine please, please explain into detail the difference bewteen the two and referance the a diagram. Please include a sketch or an image of each diagramarrow_forwardDraw left view of the first orthographic projectionarrow_forwardSketch and Describe a timing diagram for a 2 stroke diesel engine emphasis on the 2 stroke as my last answer explained 4 stroke please include a diagram or sketch.arrow_forwardA 4 ft 200 Ib 1000 Ib.ft C 2 ft 350 Ib - за в 2.5 ft 150 Ib 250 Ib 375 300 Ib Replace the force system acting on the frame. shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forwardA continuous flow calorimeter was used to obtain the calorific value of a sample of fuel and the following data collected: Mass of fuel: 2.25 kgInlet water temperature: 11 ° COutlet water temperature 60 ° CQuantity of water: 360 Liters Calorimeter efficiency: 85%Calculate the calorific value of the sample ( kJ / kg ). ive submitted this question twice and have gotten two way different answers. looking for some help thanksarrow_forward15 kg of steel ball bearings at 100 ° C is immersed in 25 kg of water at 20 ° C . Assuming no loss of heat to or from the container, calculate the final temperature of the water after equilibrium has been attained.Specific heat of steel: 0.4857 kJ / kg / ° KSpecific heat of water: 4.187 kJ / kg / ° Karrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





