Chapter 11.3, Problem 44E

a.

To determine

To show:that the hyperbolas are conjugate and sketch their graphs.

Explanation of Solution

Given information:

The hyperbola equation is $x^2-4y^2+16=0\text{ and 4}{y}^2-x^2+16=0$ .

Concept used:

Two hyperbolas are conjugate if they are in the following form,

  $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\text{ and }\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$

Proof:

first write the hyperbolas in the standard form,

  $\begin{array}{l}{x}^2-4y^2+16=0\\ \frac{x^2}{16}-\frac{y^2}{4}\text{+1=0 [divide by 16]}\\ \frac{x^2}{16}-\frac{y^2}{4}\text{=}-\text{1}\\ \text{4}{y}^2-x^2+16=0\\ \frac{y^2}{4}-\frac{x^2}{16}\text{+1=0 [divide by 16]}\\ \frac{y^2}{4}-\frac{x^2}{16}\text{=1}\\ \frac{x^2}{16}-\frac{y^2}{4}\text{=1 [multiply by -1]}\end{array}$

From the above equations it is observed that both hyperbolas are conjugate.

First write the equation in a standard form of hyperbola,

  $\frac{x^2}{16}-\frac{y^2}{4}-\text{1=0}$

Because the $x^2$ -term is positive, the hyperbola has a horizontal transverse axis;

Since here

  $\begin{array}{l}{a}^2=16\\ a=4\text{ [square root]}\\ b^2=4\\ b=2\text{ [square root]}\\ c=\sqrt{a^2+b^2}\\ c=\sqrt{16+4}\text{ [substitute]}\\ c=\sqrt{20}\text{ [add]}\\ c=2\sqrt{5}\text{ [square root]}\end{array}$

Vertices: because the $x^2$ -term of hyperbola is positive so its vertices on the x-axis.

The vertices on the x-axis are $\left(\pm a,0\right)$ ,

Now substitute $a$ by 4,

So vertices are $\left(\pm 4,0\right)$ .

Foci: because the $x^2$ -term of hyperbola is positive,

So foci are $\left(\pm c,0\right)$ ,

Now substitute $c$ by $2\sqrt{5}$ ,

So, the foci are $\left(\pm 2\sqrt{5},0\right)$ .

Asymptote: for the positive $x^2$ -term hyperbola the asymptote aregive as:

  $y=\pm \frac{b}{a}x$

Now substitute $b$ by 2 and $a$ by 4,

So asymptotes are

  $\begin{array}{l}y=\pm \frac{2}{4}x\\ y=\pm \frac{1}{2}x\end{array}$ .

Use the above information together with some additional values which is show in table below

To sketch the graph,

x	y
-4	0
-5	3.20
5	3.20
4	0

First write the equation in a standard form of hyperbola,

  $\frac{y^2}{4}-\frac{x^2}{16}-\text{1=0}$

Because the $y^2$ -term is positive, the hyperbola has a vertical transverse axis;

Since here

  $\begin{array}{l}{a}^2=4\\ a=2\text{ [square root]}\\ b^2=16\\ b=4\text{ [square root]}\\ c=\sqrt{a^2+b^2}\\ c=\sqrt{4+16}\text{ [substitute]}\\ c=\sqrt{20}\text{ [add]}\\ c=2\sqrt{5}\text{ [square root]}\end{array}$

Vertices: because the $y^2$ -term of hyperbola is positive so its vertices on the y-axis.

The vertices on the y-axis are $\left(0,\pm a\right)$ ,

Now substitute $a$ by 2,

So vertices are $\left(0,\pm 2\right)$ .

Foci: because the $y^2$ -term of hyperbola is positive,

So foci are $\left(0,\pm c\right)$ ,

Now substitute $c$ by $2\sqrt{5}$ ,

So, the foci are $\left(\pm 2\sqrt{5},0\right)$ .

Asymptote: for the positive $y^2$ -term hyperbola the asymptote aregive as:

  $y=\pm \frac{a}{b}x$

Now substitute $b$ by 4 and $a$ by 2,

So asymptotes are

  $\begin{array}{l}y=\pm \frac{2}{4}x\\ y=\pm \frac{1}{2}x\end{array}$ .

Use the above information together with some additional values which is show in table below

To sketch the graph,

x	y
-2	2.23
-1	2.06
1	2.06
2	2.23

The graph is obtained as,

  

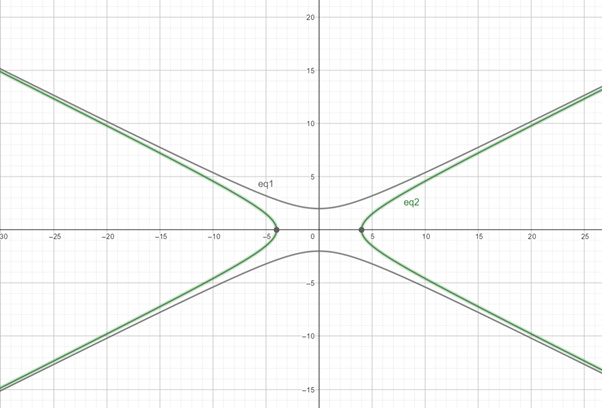
b.

To determine

To find: the common part in hyperbolas.

Answer to Problem 44E

The common part of hyperbolas is the value of c.

Explanation of Solution

The common part of hyperbolas is the value of c.

Given information:

The hyperbola equation is $x^2-4y^2+16=0\text{ and 4}{y}^2-x^2+16=0$ .

Calculation: from the part(a) it can be observed that the value of c is common in the hyperbolas.

c.

To determine

To show: that the relationship between the pair of conjugate hyperbolas.

Explanation of Solution

Given information:

The hyperbola equation is $x^2-4y^2+16=0\text{ and 4}{y}^2-x^2+16=0$ .

from the part (b) and part (a) it can be observed that,

to have a pair of conjugate hyperbolas, their c value will be same and one of the hyperbola has horizontal transverse axis and another one has to vertical transverse axis.