Chapter 11.1, Problem 17E

To determine

To find: the focus, directrix and focal diameter of the parabola and sketch the graph.

Answer to Problem 17E

Focus of parabola is $F\left(-\frac{1}{32},0\right)$ .

Directrix of parabola is $x=\frac{1}{32}$ .

Focal diameter of parabola Is $\frac{1}{8}$ .

Explanation of Solution

Focus of parabola is $F\left(-\frac{1}{32},0\right)$ .

Directrix of parabola is $x=\frac{1}{32}$ .

Focal diameter of parabola Is $\frac{1}{8}$ .

Given information:

The equation is $-8y^2=x$ .

First write the equation in a standard form of parabola,

  $\begin{array}{l}-8y^2=x\\ y^2=\frac{\left(x\right)}{-8}\text{ [divide by -8]}\\ y^2-\left(-\frac{\left(x\right)}{8}\right)\end{array}$

Comparing the standard form of the parabola to the general equation,

  $x^2-4py$

By comparing the equations it can be observed that,

  $\begin{array}{l}4p=-\frac{1}{8}\\ p=-\frac{1}{32}\text{ [divide]}\end{array}$

Directrix: the directrix of parabola is given by $x=-p$ ,

Since $p=-\frac{1}{32}$ , substitute it,

  $\begin{array}{l}x=-p\\ x=-\left(-\frac{1}{32}\right)\text{ [substitute p by -}\frac{1}{32}]\\ x=\frac{1}{32}\text{ [simplify]}\end{array}$

So the directrix of the parabola is $x=\frac{1}{32}$ .

Focus: the focus of parabola is given as $F\left(p,0\right)$ ,

Since $p=-\frac{1}{32}$ , substitute the value of $p$ ,

Thus, the focus of parabola is $F\left(-\frac{1}{32},0\right)$ .

Vertices : $\left(0,0\right)$

Focal diameter of the parabola: $\text{|4}p\text{|}$

Since $p=-\frac{1}{32}$ , substitute the value of $p$ ,

  $\begin{array}{l}\text{|4}p\text{|}\\ \text{|4}·\left(-\frac{1}{32}\right)|\text{ [substitute p by -}\frac{1}{32}]\\ \frac{1}{8}\end{array}$

So focal diameter of the parabola is $\frac{1}{8}$ .

Since the $\text{p<0}$ , so the parabola is opened to the left,

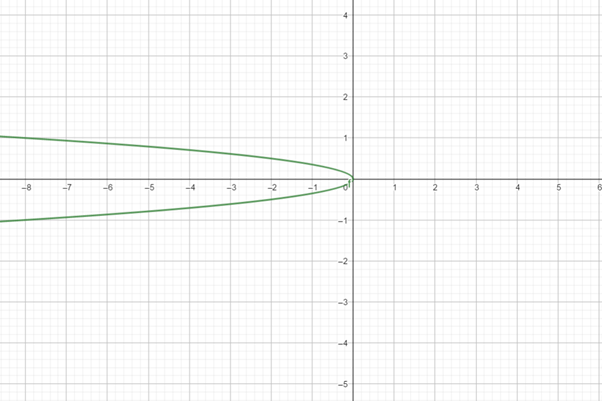
Use the above information together with some additional values which is show in table below

To sketch the graph,

x	y
-1	0.34, -0.34
-2	0.5, -0.5
-3	0.57 -0.57
-4	0.89, -0.89

The graph is obtained as: