
A gas refrigeration system using air as the working fluid has a pressure ratio of 5. Air enters the compressor at 0°C. The high-pressure air is cooled to 35°C by rejecting heat to the surroundings. The refrigerant leaves the turbine at −80°C and then it absorbs heat from the refrigerated space before entering the regenerator. The mass flow rate of air is 0.4 kg/s. Assuming isentropic efficiencies of 80 percent for the compressor and 85 percent for the turbine and using constant specific heats at room temperature, determine (a) the effectiveness of the regenerator, (b) the rate of heat removal from the refrigerated space, and (c) the COP of the cycle. Also, determine (d) the refrigeration load and the COP if this system operated on the simple gas refrigeration cycle. Use the same compressor inlet temperature as given, the same turbine inlet temperature as calculated, and the same compressor and turbine efficiencies.
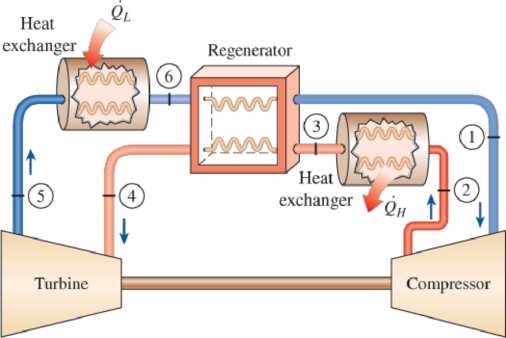
FIGURE P11–79
(a)
The effectiveness of the regenerator.
Answer to Problem 79P
The effectiveness of the regenerator is
Explanation of Solution
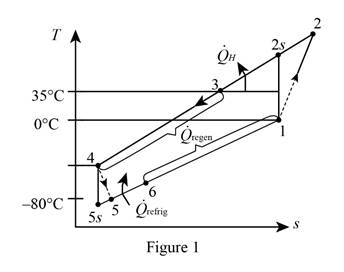
Show the T-s diagram as in Figure (1).
Express the temperature at state 2s.
Here, temperature at state 1 is
Express the temperature at state 2 from the isentropic relations.
Here, isentropic efficiency is
Express temperature at state 5s.
Here, temperature at state 4 is
Express temperature at state 4.
Here, thermal efficiency is
Express the temperature at state 6 using an energy balance.
Here, mass flow rate is
Express the effectiveness of the regenerator.
Here, enthalpy at state 3, 4 and 6 is
Conclusion:
Perform unit conversion of temperature at state 1, 3, and 5 from
Refer Table A-2, “ideal gas specific heats of various common gas”, and write the properties of air.
Substitute
Substitute
Substitute
Substitute
Solve Equations (VII) and (VIII) simultaneously by online calculator to get,
Substitute
Substitute
Hence, the effectiveness of the regenerator is
(b)
The rate of heat removal from the refrigerated space.
Answer to Problem 79P
The rate of heat removal from the refrigerated space is
Explanation of Solution
Express the rate of heat removal from the refrigerated space.
Conclusion:
Substitute
Hence, the rate of heat removal from the refrigerated space is
(c)
The COP of the gas refrigeration cycle.
Answer to Problem 79P
The COP of the gas refrigeration cycle is
Explanation of Solution
Express the net work input of the compressor.
Express the net work output of the turbine.
Express the coefficient of performance of the gas refrigeration cycle.
Conclusion:
Substitute
Substitute
Substitute
Hence, the COP of the gas refrigeration cycle is
(d)
The refrigeration load and the COP of the system.
Answer to Problem 79P
The refrigeration load is
Explanation of Solution
Show the T-s diagram as in Figure (2).

Express temperature at state 4s.
Here, temperature at state 3 is
Express temperature at state 4.
Express the refrigeration load.
Express the net work input.
Express the coefficient of performance of the system.
Conclusion:
Substitute
Substitute
Substitute
Hence, the refrigeration load is
Substitute
Substitute
Hence, the coefficient of performance of the system is
Want to see more full solutions like this?
Chapter 11 Solutions
THERMODYNAMICS LLF W/ CONNECT ACCESS
- How do i solve this problem?arrow_forwardQ4/ A compressor is driven motor by mean of a flat belt of thickness 10 mm and a width of 250 mm. The motor pulley is 300 mm diameter and run at 900 rpm and the compressor pulley is 1500 mm diameter. The shaft center distance is 1.5 m. The angle of contact of the smaller pulley is 220° and on the larger pulley is 270°. The coefficient of friction between the belt and the small pulley is 0.3, and between the belt and the large pulley is 0.25. The maximum allowable belt stress is 2 MPa and the belt density is 970 kg/m³. (a) What is the power capacity of the drive and (b) If the small pulley replaced by V-grooved pulley of diameter 300 mm, grooved angle of 34° and the coefficient of friction between belt and grooved pulley is 0.35. What will be the power capacity in this case, assuming that the diameter of the large pulley remain the same of 1500 mm.arrow_forwardYou are tasked with designing a power drive system to transmit power between a motor and a conveyor belt in a manufacturing facility as illustrated in figure. The design must ensure efficient power transmission, reliability, and safety. Given the following specifications and constraints, design drive system for this application: Specifications: Motor Power: The electric motor provides 10 kW of power at 1,500 RPM. Output Speed: The output shaft should rotate at 150 rpm. Design Decisions: Transmission ratio: Determine the necessary drive ratio for the system. Shaft Diameter: Design the shafts for both the motor and the conveyor end. Material Selection: Choose appropriate materials for the gears, shafts. Bearings: Select suitable rolling element bearings. Constraints: Space Limitation: The available space for the gear drive system is limited to a 1-meter-long section. Attribute 4 of CEP Depth of knowledge required Fundamentals-based, first principles analytical approach…arrow_forward
- - | العنوان In non-continuous dieless drawing process for copper tube as shown in Fig. (1), take the following data: Do-20mm, to=3mm, D=12mm, ti/to=0.6 and v.-15mm/s. Calculate: (1) area reduction RA, (2) drawing velocity v. Knowing that: ti: final thickness V. Fig. (1) ofthrearrow_forwardA direct extrusion operation produces the cross section shown in Fig. (2) from an aluminum billet whose diameter 160 mm and length - 700 mm. Determine the length of the extruded section at the end of the operation if the die angle -14° 60 X Fig. (2) Note: all dimensions in mm.arrow_forwardFor hot rolling processes, show that the average strain rate can be given as: = (1+5)√RdIn(+1)arrow_forward
- : +0 usão العنوان on to A vertical true centrifugal casting process is used to produce bushings that are 250 mm long and 200 mm in outside diameter. If the rotational speed during solidification is 500 rev/min, determine the inside radii at the top and bottom of the bushing if R-2R. Take: -9.81 mis ۲/۱ ostrararrow_forward: +0 العنوان use only In conventional drawing of a stainless steel wire, the original diameter D.-3mm, the area reduction at each die stand r-40%, and the proposed final diameter D.-0.5mm, how many die stands are required to complete this process. онarrow_forwardIn non-continuous dieless drawing process for copper tube as shown in Fig. (1), take the following data: Do-20mm, to=3mm, D=12mm, ti/to=0.6 and vo-15mm/s. Calculate: (1) area reduction RA, (2) drawing velocity v. Knowing that: t₁: final thickness D₁ V. Fig. (1) Darrow_forward
- A vertical true centrifugal casting process is used to produce bushings that are 250 mm long and 200 mm in outside diameter. If the rotational speed during solidification is 500 rev/min, determine the inside radii at the top and bottom of the bushing if R-2Rb. Take: 8-9.81 m/sarrow_forwardIn conventional drawing of a stainless steel wire, the original diameter D.-3mm, the area reduction at each die stand r-40%, and the proposed final diameter D₁-0.5mm, how many die stands are required to complete this process.arrow_forwardA vertical true centrifugal casting process is used to produce bushings that are 250 mm long and 200 mm in outside diameter. If the rotational speed during solidification is 500 rev/min, determine the inside radii at the top and bottom of the bushing if R-2Rb. Take: 8-9.81 m/sarrow_forward
 Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
