
Concept explainers
(a)
To find: The sketch for the curve over the given
(a)
Answer to Problem 22E
The required sketch is shown in Figure 1
Explanation of Solution
Given Data:
The given equations are,
Calculation:
Consider the given equation as,
The sketch for the above function is shown in Figure 1
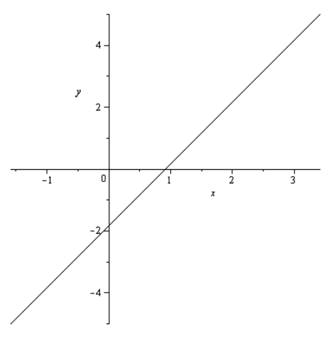
Figure 1
(b)
To find: The identification for the requested points.
(b)
Answer to Problem 22E
The rightmost point on the graph is
Explanation of Solution
Consider the graph is shown in Figure 1 the graph shows that the rightmost point on the graph is
(c)
To find: The justification that you have found the requested point by analysing an appropriate derivative.
(c)
Answer to Problem 22E
The rightmost point on the graph is
Explanation of Solution
Since, the equation is for the straight line so we do not use derivatives this equation of the line is continuous increasing function so the right most point is at
Then, the value of
Thus, rightmost point on the graph is
Chapter 11 Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Thinking Mathematically (6th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Algebra and Trigonometry (6th Edition)
Introductory Statistics
Elementary Statistics: Picturing the World (7th Edition)
- (10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z ≤ 3}. Calculate the integral f(x, y, z) dv. Earrow_forward(12 points) Let E={(x, y, z)|x²+ y² + z² ≤ 4, x, y, z > 0}. (a) (4 points) Describe the region E using spherical coordinates, that is, find p, 0, and such that (x, y, z) (psin cos 0, psin sin 0, p cos) € E. (b) (8 points) Calculate the integral E xyz dV using spherical coordinates.arrow_forward(10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z < 3}. Calculate the integral y, f(x, y, z) dV.arrow_forward
- (14 points) Let f: R3 R and T: R3. →R³ be defined by f(x, y, z) = ln(x²+ y²+2²), T(p, 0,4)=(psin cos 0, psin sin, pcos). (a) (4 points) Write out the composition g(p, 0, 4) = (foT)(p,, ) explicitly. Then calculate the gradient Vg directly, i.e. without using the chain rule. (b) (4 points) Calculate the gradient Vf(x, y, z) where (x, y, z) = T(p, 0,4). (c) (6 points) Calculate the derivative matrix DT(p, 0, p). Then use the Chain Rule to calculate Vg(r,0,4).arrow_forward(10 points) Let S be the upper hemisphere of the unit sphere x² + y²+2² = 1. Let F(x, y, z) = (x, y, z). Calculate the surface integral J F F-dS. Sarrow_forward(8 points) Calculate the following line integrals. (a) (4 points) F Fds where F(x, y, z) = (x, y, xy) and c(t) = (cost, sint, t), tЄ [0,π] . (b) (4 points) F. Fds where F(x, y, z) = (√xy, e³, xz) where c(t) = (t², t², t), t = [0, 1] .arrow_forward
- review help please and thank you!arrow_forward(10 points) Let S be the surface that is part of the sphere x² + y²+z² = 4 lying below the plane 2√3 and above the plane z-v -√3. Calculate the surface area of S.arrow_forward(8 points) Let D = {(x, y) | 0 ≤ x² + y² ≤4}. Calculate == (x² + y²)³/2dA by making a change of variables to polar coordinates, i.e. x=rcos 0, y = r sin 0.arrow_forward
- x² - y² (10 points) Let f(x,y): = (a) (6 points) For each vector u = (1, 2), calculate the directional derivative Duƒ(1,1). (b) (4 points) Determine all unit vectors u for which Duf(1, 1) = 0.arrow_forwardSolve : X + sin x = 0. By the false positioning numerical methodarrow_forwardSolve: X + sin X = 0 by the false positionining numerical methodarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





