Chapter 11.2, Problem 37E

(a)

To determine

To calculate: The velocity and speed of the particle when $t=\frac{5\pi }{4}$ .

Answer to Problem 37E

The required velocity and speed of the particle are $\langle 2\sqrt{2},0\rangle$ and $2\sqrt{2}$ respectively.

Explanation of Solution

Given information:

The position vector of the particle: $\overrightarrow{x}=\sin 4t\cos t$ , $y=\sin 2t$

Calculation:

Consider the position vector be $\overrightarrow{r}\left(t\right)$ .

So, $\overrightarrow{r}\left(t\right)=\langle \sin 4t\cos t,\sin 2t\rangle$

It is known that for a position vector $\overrightarrow{r}\left(t\right)$ of a particle, the first derivative of $\overrightarrow{r}\left(t\right)$ is the velocity vector of the particle.

So, $\begin{array}{c}\overrightarrow{v}\left(t\right)=\frac{d\left(\overrightarrow{r}\left(t\right)\right)}{dt}\\ =\frac{d}{dt}\langle \sin 4t\cos t,\sin 2t\rangle \\ =\langle \frac{d}{dt}\left(\sin 4t\cos t\right),\frac{d}{dt}\left(\sin 2t\right)\rangle \\ =\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle \end{array}$

Substitute $\frac{5\pi }{4}$ for t in the above expression.

  $\begin{array}{c}\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle =\langle 4\cos 4\left(\frac{5\pi }{4}\right)\cos \left(\frac{5\pi }{4}\right)-\sin \left(\frac{5\pi }{4}\right)\sin 4\left(\frac{5\pi }{4}\right),2\cos 2\left(\frac{5\pi }{4}\right)\rangle \\ =\langle 2\sqrt{2},0\rangle \end{array}$

Also, it is known that the magnitude of the velocity vector of a particle is known as the speed of the particle.

The magnitude of a vector $\langle \overrightarrow{a},\overrightarrow{b}\rangle$ is $\left|\langle \overrightarrow{a},\overrightarrow{b}\rangle \right|=\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}$ .

At $t=\frac{5\pi }{4}$ ; substitute $2\sqrt{2}$ for $\overrightarrow{a}$ and 0 for $\overrightarrow{b}$ in the above formula.

  $\begin{array}{c}\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}=\sqrt{{\left(2\sqrt{2}\right)}^2+{\left(0\right)}^2}\\ =\sqrt{8}\\ =2\sqrt{2}\end{array}$

Hence, the required velocity and speed of the particle are $\langle 2\sqrt{2},0\rangle$ and $2\sqrt{2}$ respectively.

(b)

To determine

To graph: The path of the particle.

Explanation of Solution

Given information:

The position vector of the particle: $\overrightarrow{x}=\sin 4t\cos t$ , $y=\sin 2t$

Calculation:

Consider the position vector be $\overrightarrow{r}\left(t\right)$ .

So, $\overrightarrow{r}\left(t\right)=\langle \sin 4t\cos t,\sin 2t\rangle$

It is known that for a position vector $\overrightarrow{r}\left(t\right)$ of a particle, the first derivative of $\overrightarrow{r}\left(t\right)$ is the velocity vector of the particle.

So, $\begin{array}{c}\overrightarrow{v}\left(t\right)=\frac{d\left(\overrightarrow{r}\left(t\right)\right)}{dt}\\ =\frac{d}{dt}\langle \sin 4t\cos t,\sin 2t\rangle \\ =\langle \frac{d}{dt}\left(\sin 4t\cos t\right),\frac{d}{dt}\left(\sin 2t\right)\rangle \\ =\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle \end{array}$

Substitute $\frac{5\pi }{4}$ for t in the above expression.

  $\begin{array}{c}\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle =\langle 4\cos 4\left(\frac{5\pi }{4}\right)\cos \left(\frac{5\pi }{4}\right)-\sin \left(\frac{5\pi }{4}\right)\sin 4\left(\frac{5\pi }{4}\right),2\cos 2\left(\frac{5\pi }{4}\right)\rangle \\ =\langle 2\sqrt{2},0\rangle \end{array}$

Also, it is known that the magnitude of the velocity vector of a particle is known as the speed of the particle.

The magnitude of a vector $\langle \overrightarrow{a},\overrightarrow{b}\rangle$ is $\left|\langle \overrightarrow{a},\overrightarrow{b}\rangle \right|=\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}$ .

At $t=\frac{5\pi }{4}$ ; substitute $2\sqrt{2}$ for $\overrightarrow{a}$ and 0 for $\overrightarrow{b}$ in the above formula.

  $\begin{array}{c}\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}=\sqrt{{\left(2\sqrt{2}\right)}^2+{\left(0\right)}^2}\\ =\sqrt{8}\\ =2\sqrt{2}\end{array}$

Thus, the velocity and speed of the particle are $\langle 2\sqrt{2},0\rangle$ and $2\sqrt{2}$ respectively when $t=\frac{5\pi }{4}$ .

The graph of the path of the particle is shown below:

  

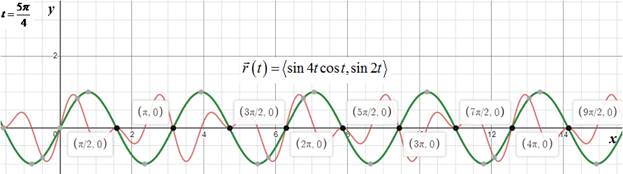
(c)

To determine

To determine: Whether the particle is moving to the left or to the right when $t=\frac{5\pi }{4}$ .

Answer to Problem 37E

The particle is moving to the right when $t=\frac{5\pi }{4}$ .

Explanation of Solution

Given information:

The position vector of the particle: $\overrightarrow{x}=\sin 4t\cos t$ , $y=\sin 2t$

Calculation:

Consider the position vector be $\overrightarrow{r}\left(t\right)$ .

So, $\overrightarrow{r}\left(t\right)=\langle \sin 4t\cos t,\sin 2t\rangle$

It is known that for a position vector $\overrightarrow{r}\left(t\right)$ of a particle, the first derivative of $\overrightarrow{r}\left(t\right)$ is the velocity vector of the particle.

So, $\begin{array}{c}\overrightarrow{v}\left(t\right)=\frac{d\left(\overrightarrow{r}\left(t\right)\right)}{dt}\\ =\frac{d}{dt}\langle \sin 4t\cos t,\sin 2t\rangle \\ =\langle \frac{d}{dt}\left(\sin 4t\cos t\right),\frac{d}{dt}\left(\sin 2t\right)\rangle \\ =\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle \end{array}$

Substitute $\frac{5\pi }{4}$ for t in the above expression.

  $\begin{array}{c}\langle 4\cos 4t\cos t-\sin t\sin 4t,2\cos 2t\rangle =\langle 4\cos 4\left(\frac{5\pi }{4}\right)\cos \left(\frac{5\pi }{4}\right)-\sin \left(\frac{5\pi }{4}\right)\sin 4\left(\frac{5\pi }{4}\right),2\cos 2\left(\frac{5\pi }{4}\right)\rangle \\ =\langle 2\sqrt{2},0\rangle \end{array}$

Also, it is known that the magnitude of the velocity vector of a particle is known as the speed of the particle.

The magnitude of a vector $\langle \overrightarrow{a},\overrightarrow{b}\rangle$ is $\left|\langle \overrightarrow{a},\overrightarrow{b}\rangle \right|=\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}$ .

At $t=\frac{5\pi }{4}$ ; substitute $2\sqrt{2}$ for $\overrightarrow{a}$ and 0 for $\overrightarrow{b}$ in the above formula.

  $\begin{array}{c}\sqrt{{\overrightarrow{a}}^2+{\overrightarrow{b}}^2}=\sqrt{{\left(2\sqrt{2}\right)}^2+{\left(0\right)}^2}\\ =\sqrt{8}\\ =2\sqrt{2}\end{array}$

Thus, the velocity and speed of the particle are $\langle 2\sqrt{2},0\rangle$ and $2\sqrt{2}$ respectively when $t=\frac{5\pi }{4}$ .

The graph of the path of the particle is shown below:

  

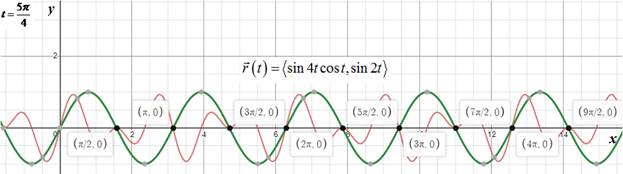
From the above graph, it is seen that the particle is moving to the right when $t=\frac{5\pi }{4}$ .