
Concept explainers
Native people throughout North and South America used a bola to hunt for birds and animals. A bola can consist of three stones, each with mass m, at the ends of three light cords, each with length ℓ. The other ends of the cords are tied together to form a Y. The hunter holds one stone and swings the other two above his head (Figure P11.41a, page 308). Both these stones move together in a horizontal circle of radius 2ℓ with speed v0. At a moment when the horizontal component of their velocity is directed toward the quarry, the hunter releases the stone in his hand. As the bola flies through the air, the cords quickly take a stable arrangement with constant 120-degree angles between them (Fig. P11.41b). In the vertical direction, the bola is in free fall. Gravitational forces exerted by the Earth make the junction of the cords move with the downward acceleration
Figure P11.41
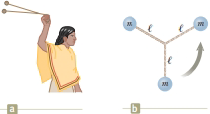
(a)
The magnitude of momentum of the bola at the moment of release and after the release.
Answer to Problem 41AP
The magnitude of momentum of the bola at the moment of release and after the release is
Explanation of Solution
At the moment of release, two stones are moving with speed
The total momentum of the is system is written as,
The total momentum has magnitude of
Conclusion:
Therefore, the magnitude of momentum of the bola at the moment of release and after the release is
(b)
The horizontal speed of the centre of mass of the bola.
Answer to Problem 41AP
The horizontal speed of the centre of mass of the bola is
Explanation of Solution
The centre of mass speed relative to the hunter is,
Mass of each stone is
Substitute
Conclusion:
Therefore, the horizontal speed of the centre of mass of the bola is
(c)
The angular momentum of the bola about its centre of mass.
Answer to Problem 41AP
The angular momentum of the bola about its centre of mass is
Explanation of Solution
The mass of each stone is
When the bola is first released, the stones are horizontally in line with two at distance
The centre of mass is given as,
This distance from the centre is not closer to the two stones: the one stone just being released at distance
The relative speed of the two stones is calculated as,
The relative speed of first stone with respect to centre of mass is given as,
The angular speed of stone 1 is,
Substitute
The angular speed of other two stones is,
Substitute
The angular speed of other two stones is equal to the angular speed of stone 1.
The total angular momentum is,
Substitute
Conclusion:
Therefore, the angular momentum of the bola about its centre of mass is
(d)
The angular speed of the bola about its centre of mass after it has settled into its Y shape.
Answer to Problem 41AP
The angular speed of the bola about its centre of mass after it has settled into its Y shape is
Explanation of Solution
As the calculation of part (c), the angular speed
The angular momentum is given as,
Rearrange the above expression for
Conclusion:
Therefore, the angular speed of the bola about its centre of mass after it has settled into its Y shape is
(e)
The kinetic energy of the bola at the instant of release.
Answer to Problem 41AP
The kinetic energy of the bola at the instant of release is
Explanation of Solution
The formula to calculate kinetic energy of the system is,
Conclusion:
Therefore, the kinetic energy of the bola at the instant of release is
(f)
The kinetic energy of the bola in its stable Y shape.
Answer to Problem 41AP
The kinetic energy of the bola in its stable Y shape is
Explanation of Solution
The formula to calculate kinetic energy of the system is,
Substitute
Conclusion:
Therefore, the kinetic energy of the bola in its stable Y shape is
(g)
The application of the conservation laws to the bola as its configuration changes.
Answer to Problem 41AP
The conservation laws are applied to the bola as it transforms its mechanical energy in to the internal energy to come in the stable state.
Explanation of Solution
The conservation laws states that the certain physical properties do not change in the course of time within an isolated physical system. There is no horizontal force act on the bola from the outside after release, so the horizontal momentum stays constant. Its center of mass moves steadily with the horizontal velocity it had at release.
No torques about its axis of rotation act on the bola, so its spin angular momentum stays constant. Internal forces cannot affect momentum conservation and angular momentum conservation, but they can affect mechanical energy. The cords pull on the stones as the stones rearrange themselves, so the cords must stretch slightly, so that energy
Conclusion:
Therefore, the conservation laws are applied to the bola as it transforms its mechanical energy in to the internal energy to come in the stable state
Want to see more full solutions like this?
Chapter 11 Solutions
Physics for Scientists and Engineers
- 3aarrow_forward44 please help with the this.arrow_forward4a Which of the following values COULD NOT be a magnitude? Choose all that apply. 626 0 -0.806 8.63 -48.5 72 131 156 4b Px = -1248 & Py = 261. Determine P.P = Qx = -1540 & Qy = 375. Determine Q.Q = 4c. T = 1105 & Ty = 425. Determine the two possible values for Tx. 4d. Uy = -38. Which of the following COULD NOT be the value of U? Choose all that apply. 10 70 72 31 47 0 75 38 4e. R has a magnitude of 165. Which of the following COULD be Rx? Choose all that apply. 165 -171 155 0 -156 -165 172 -130arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





