
Concept explainers
In Problems 1 and 2, is the matrix game strictly determined?
Whether the matrix game
Answer to Problem 1RE
The matrix game
Explanation of Solution
Consider the following matrix game.
Now, a saddle value is a payoff value which is both a row minimum and a column maximum of a payoff matrix.
Locate the saddle values.
Circle the minimum value in each row.
So, the matrix game will become,
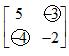
Place squares around the maximum payoff in each column of the matrix game.

In matrix game, none of the payoffs is both row minimum and column maximum.
So, the matrix game does not have a saddle value.
If the matrix game has a saddle value, then it is said to be strictly determined.
Hence, the matrix game is not strictly determined.
Want to see more full solutions like this?
Chapter 11 Solutions
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Additional Math Textbook Solutions
College Algebra with Modeling & Visualization (5th Edition)
Calculus: Early Transcendentals (2nd Edition)
Calculus: Early Transcendentals (2nd Edition)
Basic Business Statistics, Student Value Edition
Elementary Statistics (13th Edition)
Algebra and Trigonometry (6th Edition)
- Prove that Σ prime p≤x p=3 (mod 10) 1 Ρ = for some constant A. log log x + A+O 1 log x "arrow_forwardProve that, for x ≥ 2, d(n) n2 log x = B ― +0 X (금) n≤x where B is a constant that you should determine.arrow_forwardProve that, for x ≥ 2, > narrow_forwardI need diagram with solutionsarrow_forwardT. Determine the least common denominator and the domain for the 2x-3 10 problem: + x²+6x+8 x²+x-12 3 2x 2. Add: + Simplify and 5x+10 x²-2x-8 state the domain. 7 3. Add/Subtract: x+2 1 + x+6 2x+2 4 Simplify and state the domain. x+1 4 4. Subtract: - Simplify 3x-3 x²-3x+2 and state the domain. 1 15 3x-5 5. Add/Subtract: + 2 2x-14 x²-7x Simplify and state the domain.arrow_forwardQ.1) Classify the following statements as a true or false statements: Q a. A simple ring R is simple as a right R-module. b. Every ideal of ZZ is small ideal. very den to is lovaginz c. A nontrivial direct summand of a module cannot be large or small submodule. d. The sum of a finite family of small submodules of a module M is small in M. e. The direct product of a finite family of projective modules is projective f. The sum of a finite family of large submodules of a module M is large in M. g. Zz contains no minimal submodules. h. Qz has no minimal and no maximal submodules. i. Every divisible Z-module is injective. j. Every projective module is a free module. a homomorp cements Q.4) Give an example and explain your claim in each case: a) A module M which has a largest proper submodule, is directly indecomposable. b) A free subset of a module. c) A finite free module. d) A module contains no a direct summand. e) A short split exact sequence of modules.arrow_forward1 2 21. For the matrix A = 3 4 find AT (the transpose of A). 22. Determine whether the vector @ 1 3 2 is perpendicular to -6 3 2 23. If v1 = (2) 3 and v2 = compute V1 V2 (dot product). .arrow_forward7. Find the eigenvalues of the matrix (69) 8. Determine whether the vector (£) 23 is in the span of the vectors -0-0 and 2 2arrow_forward1. Solve for x: 2. Simplify: 2x+5=15. (x+3)² − (x − 2)². - b 3. If a = 3 and 6 = 4, find (a + b)² − (a² + b²). 4. Solve for x in 3x² - 12 = 0. -arrow_forward5. Find the derivative of f(x) = 6. Evaluate the integral: 3x3 2x²+x— 5. - [dz. x² dx.arrow_forward5. Find the greatest common divisor (GCD) of 24 and 36. 6. Is 121 a prime number? If not, find its factors.arrow_forward13. If a fair coin is flipped, what is the probability of getting heads? 14. A bag contains 3 red balls and 2 blue balls. If one ball is picked at random, what is the probability of picking a red ball?arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





