
The following rate constants were obtained in an experiment in which the decomposition of gaseous N2O; was studied as a function of temperature. The products were NO, and NO,.
| Temperature (K) | |
| 3.5 x 10_i | 298 |
| 2.2 x 10"4 | 308 |
| 6.8 X IO-4 | 318 |
| 3.1 x 10 1 | 328 |
Determine Etfor this reaction in kj/mol.
Interpretation:
Concept introduction:
Rate of a reaction can be explained using either growth of products or reduction of reactants. Both give the same rate, but our concern is different.
Every reaction has activation energy. To overcome this energy sometimes we should provide energy from outside. But for some reactions, we do not have to supply energy. Ambient temperature is enough that reactions. Those reactions are called spontaneous reactions.
Answer to Problem 11.57PAE
Solution:
Given:
- Chemical reaction
| Temperature/K | |
|
|
298 |
|
|
308 |
|
|
318 |
|
|
328 |
Explanation of Solution
The rate of the equation for the reaction can be written as follows.
- The only equation relating activation energy and rate constant is Arrhenius equation which is given below. The frequency factor doesn’t depend on the temperature.
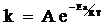
It can be written as
Therefore, at two different temperatures at
When equation 1 is subtracted from equation 2,
Formula used:
Calculation:
Want to see more full solutions like this?
Chapter 11 Solutions
Chemistry for Engineering Students
- At an electrified interface according to the Gouy-Chapman model, what types of interactions do NOT occur between the ions and the solvent according to this theory?arrow_forwardPlease predict the products for each of the following reactions. Clearly show the regiochemistry (Markovnikov vs anti-Markovnikov) and stereochemistry (syn- vs anti- or both). If a mixture of enantiomers is formed, please draw all the enantiomers. Hint: In this case you must choose the best answer to demonstrate the stereochemistry of H2 addition. 1.03 2. (CH3)2S BIZ CH₂OH 2. DMS KMnO4, NaOH ΖΗ Pd or Pt (catalyst) HBr 20 1 HBr ROOR (peroxide) HO H-SO HC 12 11 10 BH, THE 2. H2O2, NaOH Brz cold HI 19 18 17 16 MCPBA 15 14 13 A Br H₂O BH3⚫THF Brz EtOH Pd or Ni (catalyst) D₂ (deuterium) 1. Os04 2. H2O2 CH3CO3H (peroxyacid) 1. MCPBA 2. H₂O* H B + H H H "H C H H Darrow_forwardExplain how Beer’s Law can be used to determine the concentration in a selected food sample. Provide examples.arrow_forward
- Explain the importance of having a sampling plan with respect to food analysis. Explain the importance of having a sampling plan with respect to food analysis. Provide examples.arrow_forwardPlease predict the products for each of the following reactions. Clearly show the regiochemistry (Markovnikov vs anti-Markovnikov) and stereochemistry (syn- vs anti- or both). If a mixture of enantiomers is formed, please draw all the enantiomers. cold KMnO4, NaOH 2. DMS 1. 03 CH3OH Br2 1. 03 2. (CH3)2S H₂ Pd or Pt (catalyst) HBr 18 19 20 1 HBr ROOR (peroxide) H₂O H₂SO4 HCI HI 17 16 6 15 MCPBA 1. BH3 THF 2. H₂O2, NaOH 1. OsO4 2. H₂O₂ 110 CH3CO₂H (peroxyacid) 1. MCPBA 2. H₂O* Br2 H₂O BH3 THF B12 EtOH Pd or Ni (catalyst) D₂ (deuterium) Bra A B C D H OH H OH OH H OH α α α OH H OH OH фон d H "Harrow_forwardBriefly indicate the models that describe the structure of the interface: Helmholtz-Perrin, Gouy-Chapman, Stern and Grahame models.arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage Learning
World of Chemistry, 3rd editionChemistryISBN:9781133109655Author:Steven S. Zumdahl, Susan L. Zumdahl, Donald J. DeCostePublisher:Brooks / Cole / Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning





