McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 10.7, Problem 18WE
To determine
To find: the locus of the points that are equidistance from vertices of given square
Expert Solution & Answer
Answer to Problem 18WE
Required locus is the perpendicular bisector of diagonals of given square.
Explanation of Solution
Given information: Any square
Concept used: Diagonals of a square bisect each other so that this intersecting point always remains at the equal distance from all its four vertices and if this point starts moving following the given condition, it will actually be a perpendicular that passes from this intersecting point of both diagonals as shown in below figure,
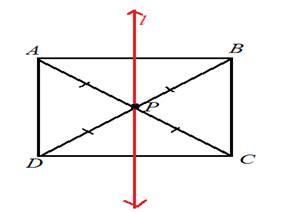
Locus of point P that always remains at equal distance from its vertices will be the red line that is perpendicular to the plane of the square and passes through the intersecting point of diagonals.
Chapter 10 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 10.1 - Prob. 1CECh. 10.1 - Prob. 2CECh. 10.1 - Prob. 3CECh. 10.1 - Prob. 4CECh. 10.1 - Prob. 5CECh. 10.1 - Prob. 6CECh. 10.1 - Prob. 1WECh. 10.1 - Prob. 2WECh. 10.1 - Prob. 3WECh. 10.1 - Prob. 4WE
Ch. 10.1 - Prob. 5WECh. 10.1 - Prob. 6WECh. 10.1 - Prob. 7WECh. 10.1 - Prob. 8WECh. 10.1 - Prob. 9WECh. 10.1 - Prob. 10WECh. 10.1 - Prob. 11WECh. 10.1 - Prob. 12WECh. 10.1 - Prob. 13WECh. 10.1 - Prob. 14WECh. 10.1 - Prob. 15WECh. 10.1 - Prob. 16WECh. 10.1 - Prob. 17WECh. 10.1 - Prob. 18WECh. 10.1 - Prob. 19WECh. 10.1 - Prob. 20WECh. 10.1 - Prob. 21WECh. 10.1 - Prob. 22WECh. 10.1 - Prob. 23WECh. 10.1 - Prob. 24WECh. 10.1 - Prob. 25WECh. 10.1 - Prob. 26WECh. 10.1 - Prob. 1MRECh. 10.1 - Prob. 2MRECh. 10.1 - Prob. 3MRECh. 10.1 - Prob. 4MRECh. 10.1 - Prob. 5MRECh. 10.1 - Prob. 6MRECh. 10.2 - Prob. 1CECh. 10.2 - Prob. 2CECh. 10.2 - Prob. 3CECh. 10.2 - Prob. 4CECh. 10.2 - Prob. 5CECh. 10.2 - Prob. 6CECh. 10.2 - Prob. 7CECh. 10.2 - Prob. 8CECh. 10.2 - Prob. 9CECh. 10.2 - Prob. 10CECh. 10.2 - Prob. 11CECh. 10.2 - Prob. 12CECh. 10.2 - Prob. 13CECh. 10.2 - Prob. 1WECh. 10.2 - Prob. 2WECh. 10.2 - Prob. 3WECh. 10.2 - Prob. 4WECh. 10.2 - Prob. 5WECh. 10.2 - Prob. 6WECh. 10.2 - Prob. 7WECh. 10.2 - Prob. 8WECh. 10.2 - Prob. 9WECh. 10.2 - Prob. 10WECh. 10.2 - Prob. 11WECh. 10.2 - Prob. 12WECh. 10.2 - Prob. 13WECh. 10.2 - Prob. 14WECh. 10.2 - Prob. 15WECh. 10.2 - Prob. 16WECh. 10.2 - Prob. 17WECh. 10.2 - Prob. 18WECh. 10.2 - Prob. 19WECh. 10.2 - Prob. 20WECh. 10.2 - Prob. 21WECh. 10.2 - Prob. 22WECh. 10.2 - Prob. 23WECh. 10.2 - Prob. 24WECh. 10.2 - Prob. 25WECh. 10.2 - Prob. 26WECh. 10.2 - Prob. 27WECh. 10.2 - Prob. 28WECh. 10.2 - Prob. 1EXCh. 10.2 - Prob. 2EXCh. 10.2 - Prob. 3EXCh. 10.3 - Prob. 1CECh. 10.3 - Prob. 2CECh. 10.3 - Prob. 3CECh. 10.3 - Prob. 4CECh. 10.3 - Prob. 5CECh. 10.3 - Prob. 6CECh. 10.3 - Prob. 1WECh. 10.3 - Prob. 2WECh. 10.3 - Prob. 3WECh. 10.3 - Prob. 4WECh. 10.3 - Prob. 5WECh. 10.3 - Prob. 6WECh. 10.3 - Prob. 7WECh. 10.3 - Prob. 8WECh. 10.3 - Prob. 9WECh. 10.3 - Prob. 10WECh. 10.3 - Prob. 11WECh. 10.3 - Prob. 12WECh. 10.3 - Prob. 13WECh. 10.3 - Prob. 14WECh. 10.3 - Prob. 15WECh. 10.3 - Prob. 16WECh. 10.3 - Prob. 17WECh. 10.3 - Prob. 1ST1Ch. 10.3 - Prob. 2ST1Ch. 10.3 - Prob. 3ST1Ch. 10.3 - Prob. 4ST1Ch. 10.3 - Prob. 5ST1Ch. 10.3 - Prob. 6ST1Ch. 10.3 - Prob. 7ST1Ch. 10.3 - Prob. 8ST1Ch. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 1MRECh. 10.3 - Prob. 2MRECh. 10.3 - Prob. 3MRECh. 10.3 - Prob. 1EXCh. 10.3 - Prob. 2EXCh. 10.4 - Prob. 1CECh. 10.4 - Prob. 2CECh. 10.4 - Prob. 3CECh. 10.4 - Prob. 4CECh. 10.4 - Prob. 5CECh. 10.4 - Prob. 6CECh. 10.4 - Prob. 7CECh. 10.4 - Prob. 1WECh. 10.4 - Prob. 2WECh. 10.4 - Prob. 3WECh. 10.4 - Prob. 4WECh. 10.4 - Prob. 5WECh. 10.4 - Prob. 6WECh. 10.4 - Prob. 7WECh. 10.4 - Prob. 8WECh. 10.4 - Prob. 9WECh. 10.4 - Prob. 10WECh. 10.4 - Prob. 11WECh. 10.4 - Prob. 12WECh. 10.4 - Prob. 13WECh. 10.4 - Prob. 14WECh. 10.4 - Prob. 15WECh. 10.4 - Prob. 16WECh. 10.4 - Prob. 17WECh. 10.4 - Prob. 18WECh. 10.4 - Prob. 19WECh. 10.4 - Prob. 20WECh. 10.4 - Prob. 21WECh. 10.5 - Prob. 1CECh. 10.5 - Prob. 2CECh. 10.5 - Prob. 3CECh. 10.5 - Prob. 4CECh. 10.5 - Prob. 5CECh. 10.5 - Prob. 6CECh. 10.5 - Prob. 7CECh. 10.5 - Prob. 8CECh. 10.5 - Prob. 9CECh. 10.5 - Prob. 10CECh. 10.5 - Prob. 11CECh. 10.5 - Prob. 1WECh. 10.5 - Prob. 2WECh. 10.5 - Prob. 3WECh. 10.5 - Prob. 4WECh. 10.5 - Prob. 5WECh. 10.5 - Prob. 6WECh. 10.5 - Prob. 7WECh. 10.5 - Prob. 8WECh. 10.5 - Prob. 9WECh. 10.5 - Prob. 10WECh. 10.5 - Prob. 11WECh. 10.5 - Prob. 12WECh. 10.5 - Prob. 13WECh. 10.5 - Prob. 14WECh. 10.5 - Prob. 15WECh. 10.5 - Prob. 16WECh. 10.5 - Prob. 17WECh. 10.5 - Prob. 18WECh. 10.5 - Prob. 1ST2Ch. 10.5 - Prob. 2ST2Ch. 10.5 - Prob. 3ST2Ch. 10.5 - Prob. 4ST2Ch. 10.5 - Prob. 5ST2Ch. 10.5 - Prob. 6ST2Ch. 10.5 - Prob. 7ST2Ch. 10.6 - Prob. 1CECh. 10.6 - Prob. 2CECh. 10.6 - Prob. 3CECh. 10.6 - Prob. 4CECh. 10.6 - Prob. 5CECh. 10.6 - Prob. 6CECh. 10.6 - Prob. 7CECh. 10.6 - Prob. 8CECh. 10.6 - Prob. 9CECh. 10.6 - Prob. 10CECh. 10.6 - Prob. 11CECh. 10.6 - Prob. 12CECh. 10.6 - Prob. 1WECh. 10.6 - Prob. 2WECh. 10.6 - Prob. 3WECh. 10.6 - Prob. 4WECh. 10.6 - Prob. 5WECh. 10.6 - Prob. 6WECh. 10.6 - Prob. 7WECh. 10.6 - Prob. 8WECh. 10.6 - Prob. 9WECh. 10.6 - Prob. 10WECh. 10.6 - Prob. 11WECh. 10.6 - Prob. 12WECh. 10.6 - Prob. 13WECh. 10.6 - Prob. 14WECh. 10.6 - Prob. 15WECh. 10.6 - Prob. 16WECh. 10.6 - Prob. 17WECh. 10.6 - Prob. 18WECh. 10.6 - Prob. 19WECh. 10.6 - Prob. 20WECh. 10.6 - Prob. 21WECh. 10.6 - Prob. 22WECh. 10.6 - Prob. 23WECh. 10.6 - Prob. 24WECh. 10.7 - Prob. 1CECh. 10.7 - Prob. 2CECh. 10.7 - Prob. 3CECh. 10.7 - Prob. 4CECh. 10.7 - Prob. 5CECh. 10.7 - Prob. 6CECh. 10.7 - Prob. 7CECh. 10.7 - Prob. 8CECh. 10.7 - Prob. 9CECh. 10.7 - Prob. 10CECh. 10.7 - Prob. 1WECh. 10.7 - Prob. 2WECh. 10.7 - Prob. 3WECh. 10.7 - Prob. 4WECh. 10.7 - Prob. 5WECh. 10.7 - Prob. 6WECh. 10.7 - Prob. 7WECh. 10.7 - Prob. 8WECh. 10.7 - Prob. 9WECh. 10.7 - Prob. 10WECh. 10.7 - Prob. 11WECh. 10.7 - Prob. 12WECh. 10.7 - Prob. 13WECh. 10.7 - Prob. 14WECh. 10.7 - Prob. 15WECh. 10.7 - Prob. 16WECh. 10.7 - Prob. 17WECh. 10.7 - Prob. 18WECh. 10.7 - Prob. 19WECh. 10.7 - Prob. 20WECh. 10.7 - Prob. 21WECh. 10.7 - Prob. 22WECh. 10.7 - Prob. 23WECh. 10.7 - Prob. 24WECh. 10.8 - Prob. 1CECh. 10.8 - Prob. 2CECh. 10.8 - Prob. 1WECh. 10.8 - Prob. 2WECh. 10.8 - Prob. 3WECh. 10.8 - Prob. 4WECh. 10.8 - Prob. 5WECh. 10.8 - Prob. 6WECh. 10.8 - Prob. 7WECh. 10.8 - Prob. 8WECh. 10.8 - Prob. 9WECh. 10.8 - Prob. 10WECh. 10.8 - Prob. 11WECh. 10.8 - Prob. 12WECh. 10.8 - Prob. 13WECh. 10.8 - Prob. 14WECh. 10.8 - Prob. 15WECh. 10.8 - Prob. 16WECh. 10.8 - Prob. 17WECh. 10.8 - Prob. 18WECh. 10.8 - Prob. 19WECh. 10.8 - Prob. 1ST3Ch. 10.8 - Prob. 2ST3Ch. 10.8 - Prob. 3ST3Ch. 10.8 - Prob. 4ST3Ch. 10.8 - Prob. 5ST3Ch. 10.8 - Prob. 6ST3Ch. 10.8 - Prob. 7ST3Ch. 10.8 - Prob. 1ECh. 10.8 - Prob. 2ECh. 10.8 - Prob. 3ECh. 10.8 - Prob. 4ECh. 10.8 - Prob. 5ECh. 10.8 - Prob. 6ECh. 10 - Prob. 1CRCh. 10 - Prob. 2CRCh. 10 - Prob. 3CRCh. 10 - Prob. 4CRCh. 10 - Prob. 5CRCh. 10 - Prob. 6CRCh. 10 - Prob. 7CRCh. 10 - Prob. 8CRCh. 10 - Prob. 9CRCh. 10 - Prob. 10CRCh. 10 - Prob. 11CRCh. 10 - Prob. 12CRCh. 10 - Prob. 13CRCh. 10 - Prob. 14CRCh. 10 - Prob. 15CRCh. 10 - Prob. 16CRCh. 10 - Prob. 17CRCh. 10 - Prob. 18CRCh. 10 - Prob. 19CRCh. 10 - Prob. 20CRCh. 10 - Prob. 21CRCh. 10 - Prob. 22CRCh. 10 - Prob. 23CRCh. 10 - Prob. 24CRCh. 10 - Prob. 25CRCh. 10 - Prob. 26CRCh. 10 - Prob. 27CRCh. 10 - Prob. 1CTCh. 10 - Prob. 2CTCh. 10 - Prob. 3CTCh. 10 - Prob. 4CTCh. 10 - Prob. 5CTCh. 10 - Prob. 6CTCh. 10 - Prob. 7CTCh. 10 - Prob. 8CTCh. 10 - Prob. 9CTCh. 10 - Prob. 10CTCh. 10 - Prob. 11CTCh. 10 - Prob. 12CTCh. 10 - Prob. 1ARCh. 10 - Prob. 2ARCh. 10 - Prob. 3ARCh. 10 - Prob. 4ARCh. 10 - Prob. 5ARCh. 10 - Prob. 6ARCh. 10 - Prob. 7ARCh. 10 - Prob. 8ARCh. 10 - Prob. 9ARCh. 10 - Prob. 10ARCh. 10 - Prob. 11ARCh. 10 - Prob. 12ARCh. 10 - Prob. 13ARCh. 10 - Prob. 14ARCh. 10 - Prob. 15ARCh. 10 - Prob. 16ARCh. 10 - Prob. 17ARCh. 10 - Prob. 18ARCh. 10 - Prob. 19ARCh. 10 - Prob. 20ARCh. 10 - Prob. 21ARCh. 10 - Prob. 22ARCh. 10 - Prob. 23ARCh. 10 - Prob. 24ARCh. 10 - Prob. 25ARCh. 10 - Prob. 26ARCh. 10 - Prob. 27ARCh. 10 - Prob. 28ARCh. 10 - Prob. 29ARCh. 10 - Prob. 30ARCh. 10 - Prob. 31ARCh. 10 - Prob. 32ARCh. 10 - Prob. 1CURCh. 10 - Prob. 2CURCh. 10 - Prob. 3CURCh. 10 - Prob. 4CURCh. 10 - Prob. 5CURCh. 10 - Prob. 6CURCh. 10 - Prob. 7CURCh. 10 - Prob. 8CURCh. 10 - Prob. 9CURCh. 10 - Prob. 10CURCh. 10 - Prob. 11CURCh. 10 - Prob. 12CURCh. 10 - Prob. 13CURCh. 10 - Prob. 14CURCh. 10 - Prob. 15CURCh. 10 - Prob. 16CURCh. 10 - Prob. 17CURCh. 10 - Prob. 18CURCh. 10 - Prob. 19CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
CHECK POINT I You deposit $1000 in a saving account at a bank that has a rate of 4%. a. Find the amount, A, of ...
Thinking Mathematically (6th Edition)
Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...
College Algebra with Modeling & Visualization (5th Edition)
Other techniques Evaluate the following limits, where a and b are fixed real numbers. 41. limx4x2164x
Calculus: Early Transcendentals (2nd Edition)
8. Effect of Blinding Among 13,200 submitted abstracts that were blindly evaluated (with authors and institutio...
Elementary Statistics
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
To calculate circumference and distance for 10 revolutions, rounded to the nearest foot.
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- 3. Construct a triangle in the Poincare plane with all sides equal to ln(2). (Hint: Use the fact that, the circle with center (0,a) and radius ln(r), r>1 in the Poincaré plane is equal to the point set { (x,y) : x^2+(y-1/2(r+1/r)a)^2=1/4(r-1/r)^2a^2 }arrow_forwardn. g. = neutral geometry <ABC = angle ABC \leq = less or equal than sqrt{x} = square root of x cLr = the line in the Poincaré plane defined by the equation (x-c)^2+y^2=r^2 1. Find the bisector of the angle <ABC in the Poincaré plane, where A=(0,5), B=(0,3) and C=(2,\sqrt{21})arrow_forward2. Let l=2L\sqrt{5} and P=(1,2) in the Poincaré plane. Find the uniqe line l' through P such that l' is orthogonal to l.arrow_forward
- Let A, B and C be three points in neutral geometry, lying on a circle with center D. If D is in the interior of the triangle ABC, then show that m(<ABC) \leq 1/2m(<ADC).arrow_forwardиз Review the deck below and determine its total square footage (add its deck and backsplash square footage together to get the result). Type your answer in the entry box and click Submit. 126 1/2" 5" backsplash A 158" CL 79" B 26" Type your answer here.arrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forward
- Select all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardQll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forward
- Q3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY