Chapter 10.4, Problem 50ES

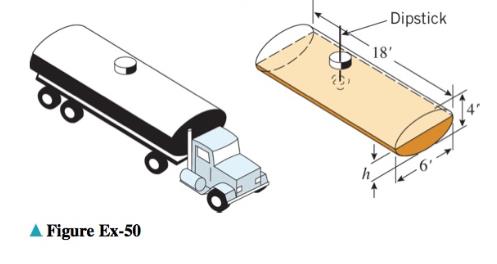
As illustrated in the accompanying figure, the tank of an oil truck is 18 ft long and has elliptical cross sections that are 6 ft wide and 4 ft high.

(a) Show that the volume V of oil in the tank (in cubic feet) when it is filled to a depth of h feet is

$V=27\left[4{\sin }^{-1}\frac{h-2}{2}+\left(h-2\right)\sqrt{4h-h^2}+2\pi \right]$

(b) Use the numerical root-finding capability of a CAS to determine how many inches from the bottom of a dipstick the calibration marks should be placed to indicate when the tank is $\frac{1}{4},\frac{1}{2},\text{and}\frac{3}{4}\text{full}.$