Chapter 10, Problem 94CP

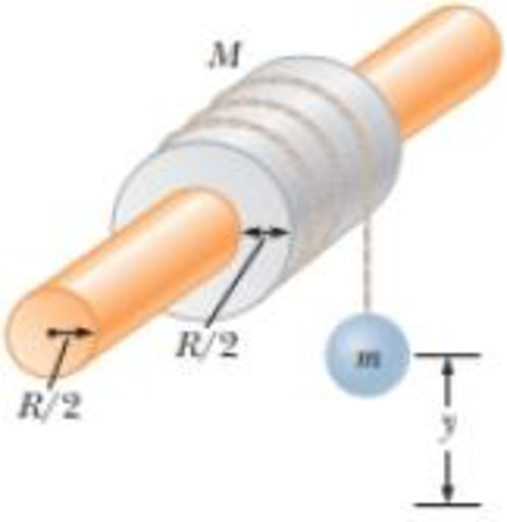
A uniform, hollow, cylindrical spool has inside radius R/2, outside radius R, and mass M (Fig. P10.47). It is mounted so that it rotates on a fixed, horizontal axle. A counterweight of mass m is connected to the end of a string wound around the spool. The counterweight falls from rest at t = 0 to a position y at time t. Show that the torque due to the friction forces between spool and axle is

${\tau }_f=R\left[m\left(g-\frac{2y}{t^2}\right)-M\frac{5y}{4t^2}\right]$

Figure P10.47