
Concept explainers
a)
To determine: The mean of each sample.
a)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean of each sample:
| Sample | ||||
| Sl. No. | 1 | 2 | 3 | 4 |
| 1 | 4.5 | 4.6 | 4.5 | 4.7 |
| 2 | 4.2 | 4.5 | 4.6 | 4.6 |
| 3 | 4.2 | 4.4 | 4.4 | 4.8 |
| 4 | 4.3 | 4.7 | 4.4 | 4.5 |
| 5 | 4.3 | 4.3 | 4.6 | 4.9 |
| Mean | 4.3 | 4.5 | 4.5 | 4.7 |
Table 1
Excel Worksheet:
Sample 1:
The mean is calculated by adding each sample points. Adding the points 4.5, 4.2, 4.2, 4.3 and 4.3 and dividing by 5 gives mean of 4.3. The same process is followed for finding mean for other samples.
Hence, the mean of each sample is shown in Table 1
b)
To determine: The mean and standard deviation when the process parameters are unknown.
b)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean and standard deviation:
Table 1 provides the mean for each sample points.
The mean is calculated by adding each mean of the samples. Adding the points 4.3, 4.5, 4.5 and 4.7 and dividing by 4 gives mean of 4.5.
The standard deviation is calculated using the above formula and substituting the values of mean in the above formula and the resultant of 0.192 is obtained.
Hence, the mean and standard deviation when the process parameters are unknown are 4.5 and 0.192.
c)
To determine: The mean and standard deviation of the sampling distribution.
c)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of mean and standard deviation of the sampling distribution:
From calculation of mean of each samples, the mean for sampling distribution can be computed, the mean for sampling distribution is 4.5 (refer equation (1)).
The standard deviation of the sampling distribution is calculated by dividing 0.192 with the square root of 5 which gives the resultant as 0.086.
Hence, the mean and standard deviation of the sampling distribution is 4.5 and 0.086 respectively.
d)
To determine: The three-sigma control limit for the process and alpha risk provided by them.
d)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Calculation of three-sigma control limit for the process:
The three-sigma control limits for the process is calculated by multiplying 3.00 with 0.086 (refer equation (2)) and the resultant is added with 4.5 to get an upper control limit which is 4.758 and subtracted to get lower control limit which is 4.242. Using z-factor table z = +3.00 corresponds to 0.4987.
The alpha risk is calculated to be as 0.0026.
Hence, the three-sigma control limits for the process are 4.758 and 4.242.
e)
To determine: The alpha risk for control limits of 4.14 and 4.86.
e)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Formula:
Calculation alpha risk for control limits of 4.14 and 4.86:
The alpha risk is calculated by dividing the difference of 4.86 and 4.5 with 0.086 which gives +4.19 which is the risk is close to zero.
Hence, the alpha risk for control limits of 4.14 and 4.86 is +4.1
f)
To determine: Whether any of the sample means are beyond the control limits.
f)
Answer to Problem 20P
Explanation of Solution
Given information:
| Sample | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Determination of whether any of the sample means are beyond the control limits:
Table 1 provides the sample means for each sample. From observation, it can be found that each sample mean are within the control limit of 4.14 and 4.86. Therefore, each sample means lies within the control limits of 4.14 and 4.86.
Hence, there are no sample means which lies beyond the control limits.
g)
To determine: Whether any of the samples are beyond the control limits.
g)
Answer to Problem 20P
Explanation of Solution
Given information:
| SAMPLE | |||
| 1 | 2 | 3 | 4 |
| 4.5 | 4.6 | 4.5 | 4.7 |
| 4.2 | 4.5 | 4.6 | 4.6 |
| 4.2 | 4.4 | 4.4 | 4.8 |
| 4.3 | 4.7 | 4.4 | 4.5 |
| 4.3 | 4.3 | 4.6 | 4.9 |
Formula:
Mean Chart:
Range Chart:
Calculation of upper and lower control limits:
| SAMPLE | ||||
| 1 | 2 | 3 | 4 | |
| 4.5 | 4.6 | 4.5 | 4.7 | |
| 4.2 | 4.5 | 4.6 | 4.6 | |
| 4.2 | 4.4 | 4.4 | 4.8 | |
| 4.3 | 4.7 | 4.4 | 4.5 | |
| 4.3 | 4.3 | 4.6 | 4.9 | |
| Mean | 4.3 | 4.5 | 4.5 | 4.7 |
| Range | .3 | .4 | .2 | .4 |
From factors of three-sigma chart, A2 = 0.58; D3 = 0; D4 = 2.11.
Mean control chart:
Upper control limit:
The Upper control limit is calculated by adding the product of 0.58 and 0.325 with 4.5 which yields 4.689.
Lower control limit:
The Lower control limit is calculated by subtracting the product of 0.58 and 0.325 with 4.5 which yields 4.311.
The UCL and LCL for mean charts are 4.686 and 4.311. (4)
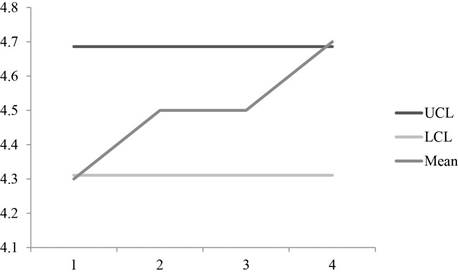
A graph is plotted using the UCL and LCL and mean values which shows the points are within the control limits.
Range control chart:
Upper control limit:
The Upper control limit is calculated by multiplying 2.11 with 0.325 which yields 0.686.
Lower control limit:
The lower control limit is calculated by multiplying 0 with 0.325 which yields 0.0.
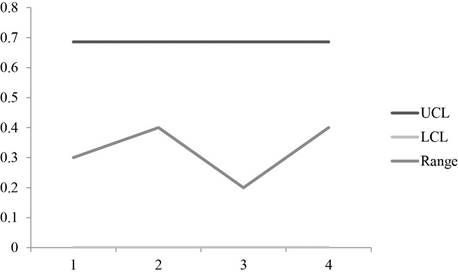
A graph is plotted using the UCL, LCL and Range values which shows that the points are within the control region.
Hence, all points are within control limits.
h)
To explain: The reason for variations in control limits.
h)
Answer to Problem 20P
Explanation of Solution
Reason for variations in control limits:
The control limits vary because in equation (3) and (4) because of the use of different measure for dispersion to measure the standard deviation and range.
Hence, the difference arises due to the use of different measures for dispersion to the measure the standard deviation and range.
i)
To determine: The control limits for the process and whether the process will be in control.
i)
Answer to Problem 20P
Explanation of Solution
Given information:
Determination of control limits of the process:
Sample mean is given in Table 1.
To calculate the control limits 0.18 is divided by root of 5 and is multiplied by 3 and the resultant is added to 4.4 to give UCL which is 4.641 and subtracted from 4.4 to get the LCL which is 4.159.
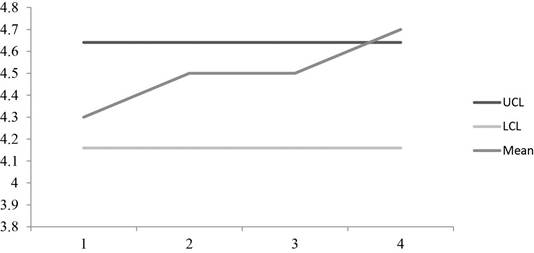
The graph shows that the some of the points are above the control limits which make the process to be out of control.
Hence, the process is out of control with UCL=4.641 and LCL=4.159.
Want to see more full solutions like this?
Chapter 10 Solutions
Loose Leaf for Operations Management (The Mcgraw-hill Series in Operations and Decision Sciences)
- northeastern insurance company is considering opening an office in the US. The two cities under consideration are going to be Philadelphia New York. Factor ratings (higher scores are better) are in the table. The best location for northeastern insurance company to open would be which with a total weighted score of ? (response rounded to two decimal places)arrow_forwardWhen football fans watch a game, they believe the other side commits more infractions on the field than does their own team. This favoritism can best be termed _____. Group of answer choices A. ethnocentrism B. the fundamental attribution error C. the affiliation bias D. marginalizationarrow_forwardWhen football fans watch a game, they believe the other side commits more infractions on the field than does their own team. This favoritism can best be termed _____. Group of answer choices ethnocentrism the fundamental attribution error the affiliation bias marginalizationarrow_forward
- Which of the following best describes the differences between egalitarianism and hierarchy as cultural values in negotiation? Group of answer choices A. Egalitarian cultures communicate directly; hierarchical cultures communicate indirectly. B. Egalitarian cultures treat people equally; hierarchical cultures discriminate among people. C. Egalitarian cultures divide things equally; hierarchical cultures divide things according to merit and status. D. Egalitarian cultures believe that status is permeable through effort and achievement; hierarchical cultures believe that superiors should take care of the needs of subordinates.arrow_forwardWhich of the following best describes the differences between individualism and collectivism as cultural values in negotiation? Group of answer choices A. Individualists see themselves as autonomous entities; collectivists see themselves in relation to others. B. Individualists prefer to work in groups; collectivists prefer to work alone. C. Individualists are cooperative; collectivists are competitive. D. Individualists focus on relationships; collectivists focus on money.arrow_forwardWhen it comes to resolving conflict, managers from hierarchical cultures prefer _____. Group of answer choices A. to attribute a disagreeable person's behavior to an underlying disposition and desire formal dispute resolution procedures B. an interests model that relies on resolving underlying conflicts C. to regulate behavior via public shaming D. to defer to a higher status personarrow_forward
- The tripartite model of culture is based on three cultural prototypes that represent negotiators’ self-views and are highly correlated with particular geographic regions. Give an example of the three. Face Dignity Honorarrow_forwardThe personality and unique character of a social group is best known as its _____ and includes the values and norms shared by its members and encompasses the structure of its social, political, economic, and religious institutions. Group of answer choices group identity group potency group stereotype culturearrow_forwardagree or disagree with this post Face - “Face” or dignity in a negotiation has been called “one of an individual’s most sacred possessions.”102 Face is the value a person places on his or her public image, reputation, and status vis-à-vis other people in the negotiation. Direct threats to face in a negotiation include making ultimatums, criticisms, challenges, and insults (Thompson, 2019). A good example of face is when I go to the negotiation table with a counterpart that is known to be difficult or not as knowledgeable about the category as they should be, my approach wouldn't be to point out their weakness, I will respect their thought process, show consideration for their perspective, all while guiding the conversation in the direction of my intended negotiation strategy in hopes to achieve my desired outcome. Dignity - endorses views such as, “People should stand up for what they believe in, even when others disagree,” and “How much a person respects oneself is far more…arrow_forward
- 16:53 ◄ Mail 5G CSTUDY_Jan25_SCMH_O...Final_20250220143201.pdf CHOOSING FORECASTING MODELS gradienting are more mode. Yet when selecting a forecasting method, the door forecasts in fact, each of the three methods has different strength and can play important ing importance of the factors, such as the index and cast model, or a unified approach, ch del runs individual series separately A galable manufacturer is facing changes with demand fuctuations due to economiyapply make changes. Comment on why this has been the case and propose a forecasting approach that can be utilised t Question 13 ashit from a batch production process to a continuous flows to enhance efficiency. Critically analyse the trade- A public hospital in Free State is experiencing increasing patient wait times due to limited operacity. The hospital management is considering either expanding existing facilities orating more efficient Question 1.5 A farming consponsible for planting grain crops in Free State As expected…arrow_forwardHow can a college basketball coach use lean system strategies to improve the team's performance and win the national championship? What wastes can be eliminated from the team's training and equipment? How can performance data be used to adjust the team's strategy and tactics?arrow_forwardHow much does self-awareness influence the Interpersonal Trust Scale's results?arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

