
Concept explainers
a)
To determine: The fraction defective in each sample.
Introduction: Quality is a measure of excellence or a state of being free from deficiencies, defects and important variations. It is obtained by consistent and strict commitment to certain standards to attain uniformity of a product to satisfy consumers’ requirement.
a)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
Excel Worksheet:

The proportion defective is calculated by dividing the number of errors with the number of samples. For sample 1, the number of errors 4 is divided by 200 which give 0.02 as prop defective.
Hence, the fraction defective is shown in Table 1.
b)
To determine: The estimation for fraction defective when true fraction defective for the process is unknown.
Introduction: Quality is a measure of excellence or a state of being free from deficiencies, defects and important variations. It is obtained by consistent and strict commitment to certain standards to attain uniformity of a product to satisfy consumers’ requirement.
b)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective:
The fraction defective is calculated when true fraction defective is unknown.
Total number of defective is calculated by adding the number of errors, (4+2+5+9) which accounts to 20
The fraction defective is calculated by dividing total number of defective with total number of observation which is 20 is divided with the product of 4 and 200 which is 0.025.
Hence, the fraction defective is 0.025.
c)
To determine: The estimate of mean and standard deviation of the sampling distribution of fraction defective for samples for the size.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
c)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Estimate of mean and standard deviation of the sampling distribution:
Mean = 0.025 (from equation (1))
The estimate for mean is shown in equation (1) and standard deviation is calculated by substituting the value which yields 0.011.
Hence, estimate of mean and standard deviation of the sampling distribution is 0.025 and 0.011.
d)
To determine: The control limits that would give an alpha risk of 0.03 for the process.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
d)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Control limits that would give an alpha risk of 0.03 for the process:
0.015 is in each tail and using z-factor table, value that corresponds to 0.5000 – 0.0150 is 0.4850 which is z = 2.17.
The UCL is calculated by adding 0.025 with the product of 2.17 and 0.011 which gives 0.0489 and LCL is calculated by subtracting 0.025 with the product of 2.17 and 0.011 which yields 0.0011.
Hence, the control limits that would give an alpha risk of 0.03 for the process are 0.0489 and 0.0011.
e)
To determine: The alpha risks that control limits 0.47 and 0.003 will provide.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
e)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Alpha risks that control limits 0.47 and 0.003 will provide:
The following equation z value can be calculated,
From z factor table, the probability value which corresponds to z = 2.00 is 0.4772, on each tail,
0.0228 is observed on each tail and doubling the value gives 0.0456 which is the alpha risk.
Hence, alpha risks that control limits 0.47 and 0.003 will provide is 0.0456
f)
To determine: Whether the process is in control when using 0.047 and 0.003.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has an upper control limit, and lower control which are used plot the time order.
f)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Calculation of fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
UCL = 0.047 & LCL = 0.003
Graph:
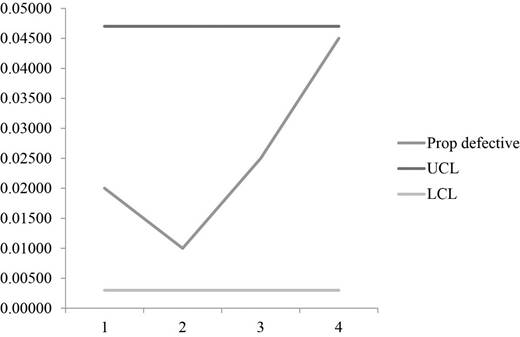
A graph is plotted using UCL, LCL and prop defective values which show that all the sample points are well within the control limits which makes the process to be in control.
Hence, the process is within control for the limits 0.047 & 0.003.
g)
To determine: The mean and standard deviation of the sampling distribution.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
g)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Long run fraction defective of the process is 0.02
Calculation of mean and standard deviation of the sampling distribution:
Fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
The mean is calculated by taking average for the proportion defective,
The values of the proportion defective are added and divided by 4 which give 0.02.
The standard deviation is calculated using the formula,
The standard deviation is calculated by substituting the values in the above formula and taking square root for the resultant value which yields 0.099.
Hence, mean and standard deviation of the sampling distribution is 0.02&0.0099.
h)
To construct: A control chart using two sigma control limits and check whether the process is in control.
Introduction:
Control chart:
It is a graph used to analyze the process change over a time period. A control chart has a upper control limit, and lower control which are used plot the time order.
h)
Answer to Problem 5P
Explanation of Solution
Given information:
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
Fraction defective in each sample:
| n | 200 | |||
| Sample | 1 | 2 | 3 | 4 |
| Number with errors | 4 | 2 | 5 | 9 |
| Prop defective | 0.02 | 0.01 | 0.025 | 0.045 |
Calculation of control limits:
The control limits are calculated using the above formula and substituting the values and taking square root gives the control limits of the UCL and LCL which are 0.0398 and 0.0002 respectively.
Graph:
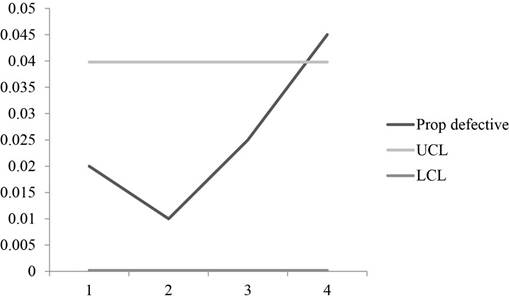
A graph is plotted using the fraction defective, UCL and LCL values which shows that one sample points is beyond the control region which makes the process to be out of control.
Hence, control chart is constructed using two-sigma control limits and the chart shows that the process is not in control.
Want to see more full solutions like this?
Chapter 10 Solutions
Loose Leaf for Operations Management (The Mcgraw-hill Series in Operations and Decision Sciences)
- A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process – assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: T = number of tables produced each week C= number of chairs produced each week According to the above information, what would the objective function be? (a) Maximize T+C (b) Maximize 120T + 80C (c) Maximize 200T+200C (d) Minimize 6T+5C (e) none of the above According to the information provided in Question 17, which of the following would be a necessary constraint in the problem? (a) T+C ≤ 40 (b) T+C ≤ 200 (c) T+C ≤ 180 (d) 120T+80C ≥ 1000…arrow_forwardAs much detail as possible. Dietary Management- Nursing Home Don't add any fill-in-the-blanksarrow_forwardMenu Planning Instructions Use the following questions and points as a guide to completing this assignment. The report should be typed. Give a copy to the facility preceptor. Submit a copy in your Foodservice System Management weekly submission. 1. Are there any federal regulations and state statutes or rules with which they must comply? Ask preceptor about regulations that could prescribe a certain amount of food that must be kept on hand for emergencies, etc. Is the facility accredited by any agency such as Joint Commission? 2. Describe the kind of menu the facility uses (may include standard select menu, menu specific to station, non-select, select, room service, etc.) 3. What type of foodservice does the facility have? This could be various stations to choose from, self-serve, 4. conventional, cook-chill, assembly-serve, etc. Are there things about the facility or system that place a constraint on the menu to be served? Consider how patients/guests are served (e.g. do they serve…arrow_forward
- Work with the chef and/or production manager to identify a menu item (or potential menu item) for which a standardized recipe is needed. Record the recipe with which you started and expand it to meet the number of servings required by the facility. Develop an evaluation rubric. Conduct an evaluation of the product. There should be three or more people evaluating the product for quality. Write a brief report of this activity • Product chosen and the reason why it was selected When and where the facility could use the product The standardized recipe sheet or card 。 o Use the facility's format or Design one of your own using a form of your choice; be sure to include the required elements • • Recipe title Yield and portion size Cooking time and temperature Ingredients and quantities Specify AP or EP Procedures (direction)arrow_forwardASSIGNMENT: Inventory, Answer the following questions 1. How does the facility survey inventory? 2. Is there a perpetual system in place? 3. How often do they do a physical inventory? 4. Participate in taking inventory. 5. Which type of stock system does the facility use? A. Minimum stock- includes a safety factor for replenishing stock B. Maximum stock- equal to a safety stock plus estimated usage (past usage and forecasts) C. Mini-max-stock allowed to deplete to a safety level before a new order is submitted to bring up inventory up to max again D. Par stock-stock brought up to the par level each time an order is placed regardless of the amount on hand at the time of order E. Other-(describe) Choose an appropriate product and determine how much of an item should be ordered. Remember the formula is: Demand during lead time + safety stock = amount to order Cost out an inventory according to data supplied. Remember that to do this, you will need to take an inventory, and will need to…arrow_forwardHuman Relations, Systems, and Organization Assignments ORGANIZATION: Review the organization chart for the facility • Draw an organization chart for the department. • . Identify and explain the relationships of different units in the organization and their importance to maintain the food service department's mission. Include a copy in your weekly submission. There is a feature in PowerPoint for doing this should you want to use it. JOB ORGANIZATION: ⚫ A job description is a broad, general, and written statement for a specific job, based on the findings of a job analysis. It generally includes duties, purpose, responsibilities, scope, and working conditions of a job along with the job's title, and the name or designation of the person to whom the employee reports. Job description usually forms the basis of job specification. • Work with your preceptor or supervisor to identify a position for which you will write a job description. Include a copy of the job description you write in your…arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

