Chapter 10, Problem 20A

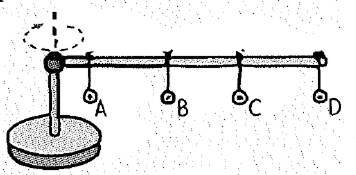
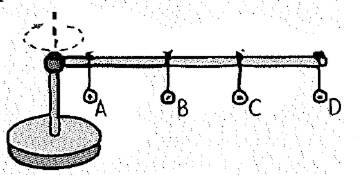
A meterstick is mounted horizontally above a turntable as shown. Identical metal washers are hung at the positions shown. The turntable and meterstick are then spun. Rank from greatest to least, the following quantities for the washers.

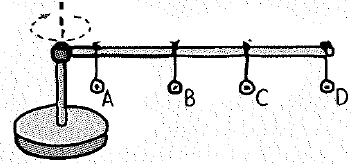
a. rotational speed

b. linear speed

c. angle the string makes with the vertical

d. inward force on each

e. outward force on each

To determine

To rank: The washer on the basis of rotational speed from greatest to least.

Answer to Problem 20A

The rank of the rotational speed from greatest to least is $A=B=C=D$ .

Explanation of Solution

Introduction:

Rotational speed is the number of rotations per unit time and is also known as angular velocity. It is represented as $\omega$ .

The given figure is shown below.

  

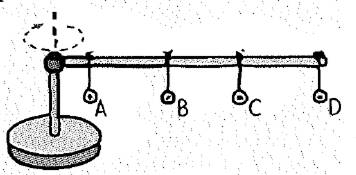
Identical metal washers are hung at the positions on a meterstick is mounted horizontally above a turntable.

The rotation of turn table rotates the metal washers in the meterstick at the same speed. Hence, the rotational speeds of the metal washers are same.

Conclusion:

Thus, the rank of the rotational speed from greatest to least is $A=B=C=D$ .

To determine

To rank: The washer on the basis of the linear speed from greatest to least.

Answer to Problem 20A

The rank of the linear speed from greatest to least is $D>C>B>A$ .

Explanation of Solution

Introduction:

The expression for the linear or tangential speed is,

  $v=r\omega$

Here, $r$ is the radial distance and $\omega$ is the angular velocity.

Tangential speed is dependent on the distance from the axis of rotation and rotational speed.

The given figure is shown below.

  

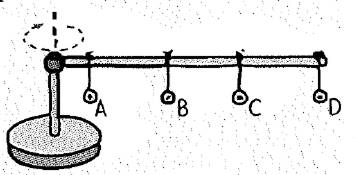
The linear speed and the radius of its circular path’ radius are directly proportional to each other.

The radius of the metal washer D is more when compared to the other washers.

The radius of the metal washer A is less when compared to the other washers.

So, the metal washer D’s linear speed is greater than the linear speed of the other washers.

Conclusion:

Thus, the rank of the linear speed from greatest to least is $D>C>B>A$ .

To determine

To rank: The washer on the basis of angle that string makes with the vertical from greatest to least.

Answer to Problem 20A

The rank of the angle the string makes with the vertical from greatest to least is $D>C>B>A$ .

Explanation of Solution

Introduction:

The force exerted on the system is directly proportional to the square of the tangential speed.

Linear speed varies with the distance from the axis of rotation.

The expression for the linear or tangential speed is,

  $v=r\omega$

Here, $r$ is the radial distance and $\omega$ is the angular velocity.

The given figure is shown below.

  

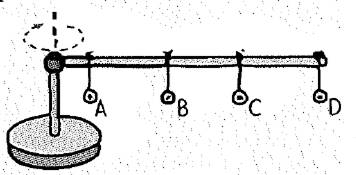
The linear speed is directly proportional to the radius of its circular path.

From part (b), the rank of the linear speed from greatest to least is $D>C>B>A$ .

The radius of the metal washer D is more when compared to the other washers.

The radius of the metal washer A is less when compared to the other washers.

By comparing the values of the angle the string makes with the vertical is $D>C>B>A$ .

Conclusion:

Thus, the rank of the angle the string makes with the vertical from greatest to least is $D>C>B>A$ .

To determine

To rank: The washer on the basis of the inward force on each from greatest to least.

Answer to Problem 20A

The rank of the inward force on each from greatest to least is $D>C>B>A$ .

Explanation of Solution

Introduction:

The expression for the centripetal force is,

  $F_{\text{c}}=\frac{m{v}^2}{r}$

Here, $m$ is the speed, $v$ is the speed, and $r$ is the radius of curvature.

The expression for the linear or tangential speed is,

  $v=r\omega$

Here, $r$ is the radial distance and $\omega$ is the angular velocity.

The given figure is shown below.

   From part (b), the rank of the linear speed from greatest to least is $D>C>B>A$ .

The centripetal force or inward force is directly proportional to the square of the linear speed.

By comparing the values of the linear speed, the centripetal force is $D>C>B>A$ .

Conclusion:

Thus, the rank of the inward force on each from greatest to least is $D>C>B>A$ .

To determine

To rank: The washers on the basis of outward force from greatest to least.

Answer to Problem 20A

The outward force is not there for the system.

Explanation of Solution

Introduction:

The expression for the centripetal force is,

  $F_{\text{c}}=\frac{m{v}^2}{r}$

Here, $m$ is the speed, $v$ is the speed, and $r$ is the radius of curvature.

The expression for the linear or tangential speed is,

  $v=r\omega$

Here, $r$ is the radial distance and $\omega$ is the angular velocity.

The given figure is shown below.

  

The centripetal force is the inward force and it is directly proportional to the square of the linear speed.

In the meterstick and turntable, there is only the centripetal or inward force act on the system.

So there is outward force doesn’t act on the system.

Conclusion:

Thus, outward force is not there for the system.