
Concept explainers
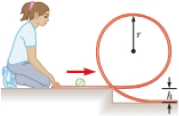
A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4.03 m/s on a horizontal section of a track as shown in Figure P10.33. It rolls around the inside of a vertical circular loop of radius r = 45.0 cm. As the ball nears the bottom of the loop, the shape of the track deviates from a perfect circle so that the ball leaves the track at a point h = 20.0 cm below the horizontal section. (a) Find the ball’s speed at the top of the loop. (b) Demonstrate that the ball will not fall from the track at the top of the loop. (c) Find the ball’s speed as it leaves the track at the bottom. (d) What If? Suppose that static friction between ball and track were negligible so that the ball slid instead of rolling. Describe the speed of the ball at the top of the loop in this situation. (e) Explain your answer to part (d).
Figure P10.33
(a)
The speed of the ball at the top of the loop.
Answer to Problem 10.64P
The speed of the ball at the top of the loop is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the translational kinetic energy of the ball at horizontal track
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the moment of inertia of the ball
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Therefore, the speed of the ball at the top of the loop is
(b)
The reason that the ball will not fall from the track at the top of the loop.
Answer to Problem 10.64P
The ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
Explanation of Solution
The radius of the circular loop is
Formula to calculate the centripetal acceleration on the ball at the top of the loop
Here,
Substitute
Thus, the centripetal acceleration act on the ball at the top of the loop is
Since the centripetal acceleration at the top of the loop is more than the acceleration due to gravity that is
Conclusion:
Therefore, the ball will not fall because the value of the centripetal acceleration is more than the acceleration due to gravity at the top point of the circular loop.
(c)
The speed of the ball as it leaves the track at the bottom.
Answer to Problem 10.64P
The speed of the ball as it leaves the track at the bottom is
Explanation of Solution
The radius of the circular loop is
Write the expression for the law of energy conservation between horizontal track and the bottom of the loop
Here,
Write the expression for the translational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at bottom point of the loop
Here,
Write the expression for the initial angular speed of the ball
Substitute
Write the expression for the potential energy of the ball at top point of the loop
Here,
Substitute
Simplify the above equation for
Conclusion:
Substitute
Thus, the speed of the ball as it leaves the track at the bottom is
(d)
The speed of the ball at the top of the loop if ball slide instead of roll.
Answer to Problem 10.64P
The speed of the ball at the top of the loop is imaginary.
Explanation of Solution
Write the expression for the law of energy conservation between horizontal track and the top of the loop
Here,
Write the expression for the rotational kinetic energy of the ball at horizontal track
Write the expression for the new translational kinetic energy of the ball at top point of the loop
Here,
Write the expression for the new potential energy of the ball at top point of the loop
Substitute
Simplify the above equation for
Substitute
Since the value inside the square root is negative that means the value is imaginary. This condition is impractical.
Thus, the speed of the ball at the top of the loop is imaginary.
Conclusion:
Therefore, the speed of the ball at the top of the loop is imaginary. It can’t be calculated.
(e)
The explanation of the solution of part (d).
Answer to Problem 10.64P
The ball has not sufficient energy to arrive at top of the circular loop.
Explanation of Solution
The velocity comes out to be imaginary in part (d) that indicates the situation in impossible because as the boll slide instead of rolling, the ball have only translational kinetic energy which is insufficient for the ball to reach the top point on the circular loop.
Thus, the ball did not arrive at the top point of the loop.
Conclusion:
Therefore, the ball has not sufficient energy to arrive at top of the circular loop.
Want to see more full solutions like this?
Chapter 10 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- In the comics Thor flies by spinning his hammer really fast from a leather strap at the end of the handle, letting go, then grabbing it and having it pull him. If Thor wants to reach escape velocity (velocity needed to leave Earth’s atmosphere), he will need the linear velocity of the center of mass of the hammer to be 11,200 m/s. A) If the distance from the end of the strap to the center of the hammer is 0.334 m, what angular velocity does Thor need to spin his hammer at to reach escape velocity? b) If the hammer starts from rest what angular acceleration does Thor need to reach that angular velocity in 4.16 s? c) While the hammer is spinning at its maximum speed what impossibly large tension does the leather strap, which the hammer is spinning by, exert when the hammer is at its lowest point? The hammer has a total mass of 20.0kg.arrow_forwardThe car goes from driving straight to spinning at 10.6 rev/min in 0.257 s with a radius of 12.2 m. The angular accleration is 4.28 rad/s^2. During this flip Barbie stays firmly seated in the car’s seat. Barbie has a mass of 58.0 kg, what is her normal force at the top of the loop?arrow_forwardConsider a hoop of radius R and mass M rolling without slipping. Which form of kinetic energy is larger, translational or rotational?arrow_forward
- A roller-coaster vehicle has a mass of 571 kg when fully loaded with passengers (see figure). A) If the vehicle has a speed of 22.5 m/s at point A, what is the force of the track on the vehicle at this point? B) What is the maximum speed the vehicle can have at point B, in order for gravity to hold it on the track?arrow_forwardThis one wheeled motorcycle’s wheel maximum angular velocity was about 430 rev/min. Given that it’s radius was 0.920 m, what was the largest linear velocity of the monowheel?The monowheel could not accelerate fast or the rider would start spinning inside (this is called "gerbiling"). The maximum angular acceleration was 10.9 rad/s2. How long, in seconds, would it take it to hit maximum speed from rest?arrow_forwardIf points a and b are connected by a wire with negligible resistance, find the magnitude of the current in the 12.0 V battery.arrow_forward
- Consider the two pucks shown in the figure. As they move towards each other, the momentum of each puck is equal in magnitude and opposite in direction. Given that v kinetic energy of the system is converted to internal energy? 30.0° 130.0 = green 11.0 m/s, and m blue is 25.0% greater than m 'green' what are the final speeds of each puck (in m/s), if 1½-½ t thearrow_forwardConsider the blocks on the curved ramp as seen in the figure. The blocks have masses m₁ = 2.00 kg and m₂ = 3.60 kg, and are initially at rest. The blocks are allowed to slide down the ramp and they then undergo a head-on, elastic collision on the flat portion. Determine the heights (in m) to which m₁ and m2 rise on the curved portion of the ramp after the collision. Assume the ramp is frictionless, and h 4.40 m. m2 = m₁ m hm1 hm2 m iarrow_forwardA 3.04-kg steel ball strikes a massive wall at 10.0 m/s at an angle of 0 = 60.0° with the plane of the wall. It bounces off the wall with the same speed and angle (see the figure below). If the ball is in contact with the wall for 0.234 s, what is the average force exerted by the wall on the ball? magnitude direction ---Select--- ✓ N xarrow_forward
- You are in the early stages of an internship at NASA. Your supervisor has asked you to analyze emergency procedures for extravehicular activity (EVA), when the astronauts leave the International Space Station (ISS) to do repairs to its exterior or perform other tasks. In particular, the scenario you are studying is a failure of the manned-maneuvering unit (MMU), which is a nitrogen-propelled backpack that attaches to the astronaut's primary life support system (PLSS). In this scenario, the astronaut is floating directly away from the ISS and cannot use the failed MMU to get back. Therefore, the emergency plan is to take off the MMU and throw it in a direction directly away from the ISS, an action that will hopefully cause the astronaut to reverse direction and float back to the station. You have the following mass data provided to you: astronaut: 78.1 kg, spacesuit: 36.8 kg, MMU: 115 kg, PLSS: 145 kg. Based on tests performed by astronauts floating "weightless" inside the ISS, the most…arrow_forwardThree carts of masses m₁ = 4.50 kg, m₂ = 10.50 kg, and m3 = 3.00 kg move on a frictionless, horizontal track with speeds of V1 v1 13 m 12 mq m3 (a) Find the final velocity of the train of three carts. magnitude direction m/s |---Select--- ☑ (b) Does your answer require that all the carts collide and stick together at the same moment? ○ Yes Ο Νο = 6.00 m/s to the right, v₂ = 3.00 m/s to the right, and V3 = 6.00 m/s to the left, as shown below. Velcro couplers make the carts stick together after colliding.arrow_forwardA girl launches a toy rocket from the ground. The engine experiences an average thrust of 5.26 N. The mass of the engine plus fuel before liftoff is 25.4 g, which includes fuel mass of 12.7 g. The engine fires for a total of 1.90 s. (Assume all the fuel is consumed.) (a) Calculate the average exhaust speed of the engine (in m/s). m/s (b) This engine is positioned in a rocket body of mass 70.0 g. What is the magnitude of the final velocity of the rocket (in m/s) if it were to be fired from rest in outer space with the same amount of fuel? Assume the fuel burns at a constant rate. m/sarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





