
Concept explainers
For a particle in a state having the wavefunction
(a)
(c)
(e)
Plot the probabilities versus
(a)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.26E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above expression is simplified as follows.
The probability for the particle having wavefunction
(b)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.26E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above expression is simplified as follows.
The probability for the particle having wavefunction
(c)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.26E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above expression is simplified as follows.
The probability for the particle having wavefunction
(d)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.26E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above expression is simplified as follows.
The probability for the particle having wavefunction
(e)
Interpretation:
The probability for the particle having wavefunction
Concept introduction:
For the normalization of the wavefunction, the wavefunction is integrated as a product of its conjugate over the entire limits. It is expressed by the equation as given below.
Where,
•
•
•
Answer to Problem 10.26E
The probability for the particle having wavefunction
Explanation of Solution
For the probability of the wavefunction the expression is as follows.
Where,
•
•
•
•
Substitute the values in the above equation as follows.
The above expression is simplified as follows.
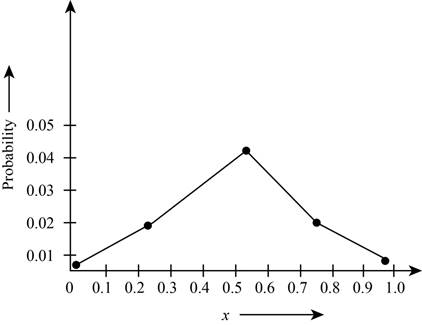
Theplot the probabilities versus

Figure 1
The plot shows the probability for the given wave function. According to this plot, the probability of finding the particle is maximum in the range of
The probability for the particle having wavefunction
Want to see more full solutions like this?
Chapter 10 Solutions
Physical Chemistry
- When talking about the acidity of carboxylic acids, is it the same thing to say higher or stronger acidity?arrow_forwardUsing the following two half-reactions, determine the pH range in which $NO_2^-\ (aq)$ cannot be found as the predominant chemical species in water.* $NO_3^-(aq)+10H^+(aq)+8e^-\rightarrow NH_4^+(aq)+3H_2O(l),\ pE^{\circ}=14.88$* $NO_2^-(aq)+8H^+(aq)+6e^-\rightarrow NH_4^+(aq)+2H_2O(l),\ pE^{\circ}=15.08$arrow_forwardIndicate characteristics of oxodec acid.arrow_forward
- What is the final product when hexanedioic acid reacts with 1º PCl5 and 2º NH3.arrow_forwardWhat is the final product when D-galactose reacts with hydroxylamine?arrow_forwardIndicate the formula of the product obtained by reacting methyl 5-chloro-5-oxopentanoate with 1 mole of 4-penten-1-ylmagnesium bromide.arrow_forward
 Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
