Introductory Mathematics for Engineering Applications
1st Edition
ISBN: 9781118141809
Author: Nathan Klingbeil
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 1, Problem 3P
The spring force F and displacement x for a close-wound tension spring arc measured as shown in Fig. P1.3.
The spring force F and displacement x satisfy the linear equation
(a) Using the given data, find the equation of the line for the spring force F as a function of the displacement x, and determine the values of the spring constant k and preload Fi.
(b) Sketch the graph of F as a function of x and dearly indicate both the spring constant k and preload Fi.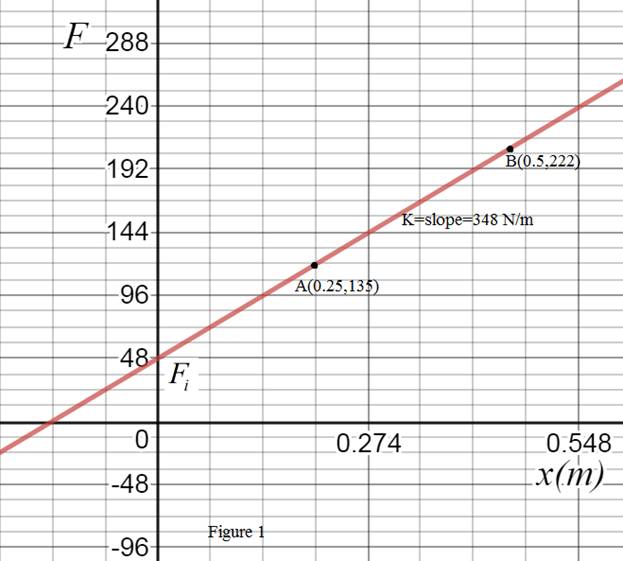 
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule08:20
Students have asked these similar questions
5. How many numbers can you make out of the digits 1, 2, 3, 4, 6 if the rule is that every digit has to be
larger than the digit preceding it? For example 124 is ok, 122 is not ok. Every digit can be used only
once, but you do not have to use every digit. A tree might help.
Can you help me with f and g?What they are asking is, what do you shade in? Not the power set. At least for F
Q3
3 Points
1 0 2
4
0 6
01 5
-
-1
0
10
00 0
0
1 1
The reduced row echelon form of the augmented matrix of a linear system is given above.
Describe the solution set of this linear system in parametric vector form.
Please select file(s) Select file(s)
Save Answer
Chapter 1 Solutions
Introductory Mathematics for Engineering Applications
Ch. 1 - A constant force F=2N is applied to a spring and...Ch. 1 - The spring force F and displacement x for a...Ch. 1 - The spring force F and displacement x for a...Ch. 1 - In a bolted connection shown in Fig. P1.4. the...Ch. 1 - Repeat problem P1.14 for the data given in Fig...Ch. 1 - The velocity v (t ) of a ball thrown upward...Ch. 1 - The velocity v (r ) of a ball thrown upward...Ch. 1 - A model rocket is fired in the vertical plane. The...Ch. 1 - A model rocket is fired in the vertical plane. The...Ch. 1 - The velocity of a vehicle is measured at two...
Ch. 1 - The velocity of a vehicle is measured at two...Ch. 1 - The velocity v (t ) of a vehicle during braking is...Ch. 1 - A linear trajectory is planned for a robot to pick...Ch. 1 - The acceleration of the linear trajectory of...Ch. 1 - The temperature distribution in a well-insulated...Ch. 1 - The temperature distribution in a well-insulated...Ch. 1 - The voltage-current relatonship for the cicuit...Ch. 1 - A voltage source Vs is used to apply two different...Ch. 1 - Repeat problem P1-18 for the data shown in Fig,...Ch. 1 - Repeat problem P1-18 for the data shown in Fig...Ch. 1 - A linear model of a diode is shown in Fig. P1.21....Ch. 1 - Repeat Problem P1-21 for the data given in Fig....Ch. 1 - The output voltage, v0, of the Op-Amp circuit...Ch. 1 - The output voltage, v0, of the Op-Amp circuit...Ch. 1 - A DC motor is driving an inertial load JL shown in...Ch. 1 - Repeat problem P1-25 for the data shown in Fig....Ch. 1 - In the active region, the output voltage v0 of the...Ch. 1 - Repeat problem P1-27 for the data given in Fig,...Ch. 1 - An actuator used in a prosthetic arm can produce...Ch. 1 - The following two measurements of maximum heart...Ch. 1 - The electrical activity of muscles can he...Ch. 1 - A civil engineer needs to establish the elevation...Ch. 1 - A thermocouple is a temperature measurement...Ch. 1 - The voltage across a thermocouple is calibrated...Ch. 1 - An iron-constantan thermocouple is calibrated by...Ch. 1 - Prob. 36PCh. 1 - Repeat problem P1-36 for the data shown in Fig....Ch. 1 - To determine the concentration of a purified...Ch. 1 - Repeat problem P1-38 lithe absorption-...Ch. 1 - A chemistry student is performing in experiment to...Ch. 1 - To obtain the linear relationship between the...Ch. 1 - A thermostat control with dial marking from 0 to...Ch. 1 - In a pressure-fed journal bearing, forced cooling...
Additional Math Textbook Solutions
Find more solutions based on key concepts
3. Voluntary Response Sample What is a voluntary response sample, and why is such a sample generally not suitab...
Elementary Statistics
In Exercises 1–18, find dy/dx.
1. y = −10x + 3 cos x
University Calculus: Early Transcendentals (4th Edition)
Finding the Margin of Error In Exercises 33 and 34, use the confidence interval to find the estimated margin of...
Elementary Statistics: Picturing the World (7th Edition)
In Exercises 11–14, use the population of {34, 36, 41, 51} of the amounts of caffeine (mg / 12 oz ) in Coca-Col...
Elementary Statistics (13th Edition)
Explain why or why not Determine whether the following statements are true and give an explanation or counterex...
Calculus: Early Transcendentals (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- 3. Suppose you have 12 professors in a department and you have to chose members of departmental committees. (a) How many ways can you pick members for one 4 people committee? (b) How many ways can you pick members for two different 4 people committees if no-one can serve on both committees? (c) How many ways can you pick members for two different 4 people committees if people can serve on both committees? (d) How about if you need members for a 4 person, a 5 person, and a 3 person committee, people cannot serve on more than one committee? (e) How about if you need members for a 4 person, a 5 person, and a 3 person committee, people can serve on more than one committee? (f) How about if you need members for a 4 person, a 5 person, and a 3 person committee, people cannot serve on more than one committee, and the first person chosen for each committee serves as chair?arrow_forwardQ4 3 Points 1 Let A = 2 3 7 5 11 Give one nontrivial solution X of the homogeneous system Ax = 0. (Your vector x should have explicit numbers as its entries, as opposed to variables/parameters). Show your work for how you found it. Please select file(s) Select file(s) Save Answerarrow_forward4. Assume that a risk-free money market account is added to the market described in Q3. The continuously compounded rate of return on the money market account is log (1.1). (i) For each given μ, use Lagrange multipliers to determine the proportions (as a function of μ) of wealth invested in the three assets available for the minimum variance portfolio with expected return μ. (ii) Determine the market portfolio in this market and calculate its Sharp ratio.arrow_forward
- 3. A market consists of two risky assets with rates of return R₁ and R2 and no risk-free asset. From market data the following have been estimated: ER₁ = 0.25, ER2 = 0.05, Var R₁ = 0.01, Var R2 = 0.04 and the correlation between R1 and R2 is p = -0.75. (i) Given that an investor is targeting a total expected return of μ = 0.2. What portfolio weights should they choose to meet this goal with minimum portfolio variance? Correct all your calculations up to 4 decimal points. (ii) Determine the global minimum-variance portfolio and the expected return and variance of return of this portfolio (4 d.p.). (iii) Sketch the minimum-variance frontier in the μ-σ² plane and indicate the efficient frontier. (iv) Without further calculation, explain how the minimum variance of the investor's portfolio return will change if the two risky assets were independent.arrow_forward2. A landlord is about to write a rental contract for a tenant which lasts T months. The landlord first decides the length T > 0 (need not be an integer) of the contract, the tenant then signs it and pays an initial handling fee of £100 before moving in. The landlord collects the total amount of rent erT at the end of the contract at a continuously compounded rate r> 0, but the contract stipulates that the tenant may leave before T, in which case the landlord only collects the total rent up until the tenant's departure time 7. Assume that 7 is exponentially distributed with rate > 0, λ‡r. (i) Calculate the expected total payment EW the landlord will receive in terms of T. (ii) Assume that the landlord has logarithmic utility U(w) = log(w - 100) and decides that the rental rate r should depend on the contract length T by r(T) = λ √T 1 For each given λ, what T (as a function of X) should the landlord choose so as to maximise their expected utility? Justify your answer. Hint. It might be…arrow_forwardPlease ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forward
- Consider the proof below: Proposition: If m is an even integer, then 5m +4 is an even integer. Proof: We see that |5m+4=10n+4 = 2(5n+2). Therefore, 5m+4 is an even integer. **Note: you may assume the proof is valid, just poorly written. Based upon the Section 1.3 screencast and the reading assignment, select all writing guidelines that are missing in the proof. Proof begins by stating assumptions ✓ Proof has an invitational tone/uses collective pronouns Proof is written in complete sentences Each step is justified ☐ Proof has a clear conclusionarrow_forwardThe general solution X'=Ax is given. Discuss the nature of the solutions in a neighborhood of (0,0) -2-2 (²) |a) A = (23) X(A) = (₁ (fi)e* + (2 (2) eht -2-5arrow_forwardPlease ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forward
- Using the method of joints, determine the force in each member of the truss shown. Summarize the results on a force summation diagram, and indicate whether each member is in tension or compression. You may want to try the "quick" method hod.16 8m T or C CD CE AB EF BF гид B 6m i force in CE only (change top force to 8kn) 8 KN 8kNarrow_forwardNo chatgpt pls will upvotearrow_forwardPlease ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY