Chapter 1, Problem 15PS

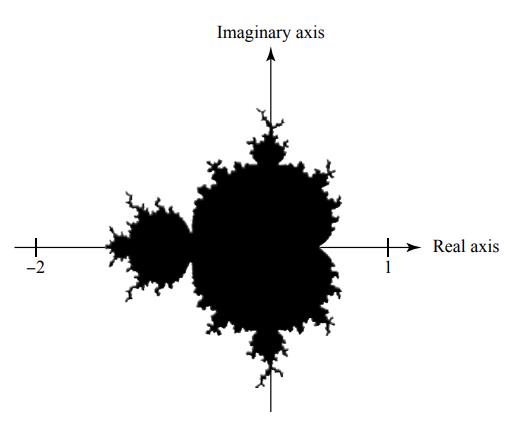
The Mandelbrot Set A fractal is a geometric figure that consists of a pattern that is repeated infinitely on a smaller and smaller scale. The most famous fractal is the Mandelbrot Set, named after the Polish-born mathematician Benoit Mandelbrot $\left(1924-2010\right).$ To draw the Mandelbrot Set, consider the sequence of numbers below.

$c,c^2+c,{\left(c^2+c\right)}^2+c,{\left[{\left(c^2+c\right)}^2+c\right]}^2+c,\mathrm{...}$

The behavior of this sequence depends on the value of the complex number $c.$ If the sequence is bounded (the absolute value of each number in the sequence,

$\mid a+bi\mid =\sqrt{a^2+b^2}$

is less than some fixed number $N$ ), then the complex number c is in the Mandelbrot Set, and if the sequence is unbounded (the absolute value of the terms of the sequence become infinitely large), then the complex number $c$ is not in the Mandelbrot Set. Determine whether the complex number $c$ is in the Mandelbrot Set.

$\left(\text{a}\right)c=i$

$\left(\text{b}\right)c=1+i$

$\left(\text{c}\right)c=-2$

The figure below shows a graph of the Mandelbrot Set, where the horizontal and vertical axes represent the real and imaginary parts of $c$, respectively.