Show that the one-particle partition function Z₁ for a 2D ideal gas confined to area A is: A Z₁ 22 th
Q: A particle of mass M moves in a periodic potential with the form, V Vo [15 2 16 2πx 1 - cos + 16 :…
A: First, we need to approximate the potential close to x = 0. We can use the given approximation for…
Q: The probability p; of occupying an available state j is: Pj 9je-BEj Z where g; is the degeneracy of…
A: Step 1:The probability of occupying states i and k, respectively…
Q: A system consisting of six indistinguishable particles obeys the Fermi-Dirac statistics. This system…
A: Given that there are 6 particles which follows Fermi-dirac statistics. Degeneracy of each level is…
Q: Estimate the relative probabilities of various velocities. Pick a small interval ∆vx = 0.002vx rms.…
A: Given: Small interval dvx=0.002vxrms . It is known that the probability g(vx )dvx that the…
Q: A system has two normal modes of vibration, with frequencies @, and @₂ = 2w₁ . What is the…
A:
Q: A 3kg ball is traveling 10m/s diagonally when it strikes a horizontal surface. The ball bounces off…
A:
Q: Show that for an ideal Fermi-Dirac gas that (kT\ 4 57? (kT 1+ 12 2 2 Νμο P-5 V 16 \Ho)
A:
Q: For 3D the partition function will be Z3D Z³ = exp{-(hu) KBT hw 1- exp{- KBT which is the partition…
A: Since for single particle the partition function is given.
Q: A particle of mass m is bound in a one-dimensional well with one impenetrable wall. The potential…
A:
Q: (20.7) The energy E of a system of three independent harmonic oscillators is given by 1 E = (Nx + ½…
A:
Q: 1000 molecules are bouncing between wells separated by enthalpy gaps H1= 1 ·10-20 J and H2 = 2…
A:
Q: E △E=2×10-21 J DE=10-21 J E2 E1 Eo
A:
Q: Suppose we are in the NPT ensemble, and that the entropy S = S(L) depends on the length of a…
A: Given: We are in the NPT ensemble The entropy S = S(L) depends on the length of a…
Q: Starting from the definition of the partition function, Z = Ei e-Bei, prove the following: a) (E): =…
A: We know that expextation value of a physical quantity is average value of that physical quantity…
Q: An unfortunate astronaut loses his grip during a spacewalk and finds himself floating away from the…
A: Using conservation of momentum ma+mbvi=mavaf+mbvbfvbf=ma+mbvi-mavafmb
Q: An atom has energy levels 0, E, 2E, Calculate the canonical partition function of a system composed…
A: The canonical partition function for an atom is given by, Where, gi be defined as the degeneracy of…
Q: PV 1/V (1) 1/V→ (iii) (iv) Boyle's law may be best expressed by O the top left curve any of the…
A: Introduction: Boyle's law states that the pressure is inversely proportional to the volume of the…
Q: Consider the semiclassical model of N particles with two energy levels (0 and e > 0). Suppose that…
A:
Q: A particle is in a box with infinitely rigid walls. The walls are at x = -L/2 and x = +L/2.Show that…
A: Schrodinger equation of motion is written as -h22md2ψdx2+vxψ=Eψvx=0, x = -L/2 and x = +L/2∞,…
Q: Show that the Maxwell speed distribution function F(v) approaches zero by taking the limit as v → 0…
A: The air molecules surrounding us aren't all traveling at an equivalent speed, albeit the air is…
Q: Given the internal energy U and entropy S of N weakly interacting particles in a closed system with…
A: It is given that, The internal energy is given by,…
Q: The derivative of the function at t = 1 is closest to: See Image:
A:
Q: Show that at high enough temperatures (where KBT » ħw) the partition function of a simple quantum…
A:
Q: Consider a classical ideal gas in three dimensions, with N indistin- guishable atoms confined in a…
A: As per the policy I will answer only the 1st three subparts of this question. Let us now practice…

Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Hello,whats the mean of this sign?
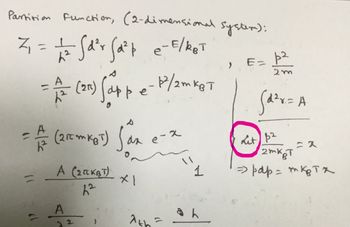
- Problem 1: Consider a classical ideal gas in three dimensions, with N indistinguishable atoms confined in a box of volume N³. Assume the atoms have zero spin and neglect any internal degrees of freedom. Starting from the energy levels of a single atom in a box, find: (a) The Helmholtz free energy F' Hint: ſ. -ax² d.x e Va (b) The entropy o (c) The pressure pFor 3D free electron gas, the density of states counts the number of degenerate electron states dn per energy interval dE around a given energy E as g(E): = dn dE 3 (2m₂)2V 1 E2 2π²ħ³ At absolute zero temperature, N electrons can fill up all low lying energy levels (following Pauli exclusion principle) up to a given energy level E called Fermi energy. From the density of states, what is the relation between the total electron states N below a given energy E? Use this result to show that the Fermi energy EF is given by - - 2010 (307² M)³ ħ² 3π²N\3 EF 2me VThe value of a partition function roughly represents the maximum energy of the states at a given temperature. O True False
- Please help to prove this to be trueConsider a classical ideal gas of N diatomic heterogeneous molecules at temperature T. The charac- teristic rotational energy parameter is € = 1 and the natural frequency of vibrations is wo. Consider the temperature region where T≫er/kB, but T is of the order of ħwo/kB. Ignore contributions from all other internal modes. Calculate the canonical partition function, the average energy, and the heat capacity at constant volume, Cv.Calculate the partition function of a two-level system at 25 °C with an energy gap of 10-2¹ J, assuming: a) Both states are non-degenerate. b) The ground state is non-degenerate, and the excited state is 3-fold degenerate.
- For a system of particles at room temperature (300K), what value must & be before the Fermi-Dirac, Bose-Einstein, and Maxwell-Boltzmann distributions agree within 0.1% ? Justify your answer.A diatomic gas molecule can be in one of two vibrational energy levels, separated by 0.1 eV. Give the probabilities to be in either state and use these to calculate their relative populations at room temperature, T≈ 300 K. [You may use that kB ≈ 8.6 × 10−5 K eV−1]Consider a three-dimensional infinite-well modeled as a cube of dimensions L x L x L. The length L is such that the ground state energy of one electron confined to this box is 0.50eV. (a) Write down the four lowest energy states and evaluate their corresponding degeneracy. (b) If 15 (total) electrons are placed in the box, find the Fermi energy of the system. (c) What is the total energy of the 15-electron system? (d) How much energy would be required to lift an electron from Fermi energy of part (b) to the first excited state? Need full detailed answers and explanations to understand the concept.